Необходимые условия экстремума. Если функция достигает экстремума в точке ,
то её частные производные в этой точке равны нулю или не существуют:
Точки, в которых частные производные первого порядка равны нулю или не существуют называются критическими точками функции.
Для нахождения экстремума функции в данной области необходимо каждую критическую точку подвергнуть дополнительному исследованию.
Достаточные условия экстремума. Пусть функция в некоторой области D имеет непрерывные частные производные и точка есть критическая точка данной функции. Обозначим:
и .
Тогда:
1) Если , то функция в точке имеет минимум;
2) Если , то функция в точке имеет максимум;
3) Если , то в точке функция экстремума не имеет.
Необходимые и достаточные условия существования экстремума










 Решение задач по теме Площади фигур
Решение задач по теме Площади фигур Презентация по математике.
Презентация по математике. Дифференциальное исчисление
Дифференциальное исчисление Углы. Измерение углов. Построение углов. 5 класс
Углы. Измерение углов. Построение углов. 5 класс Математика.Тема урока: Числа от 1 до 10.
Математика.Тема урока: Числа от 1 до 10. Замена произведения чисел их суммой
Замена произведения чисел их суммой Неопределенный интеграл
Неопределенный интеграл Задачи на переливание жидкости
Задачи на переливание жидкости Теория графов: основные понятия и определения
Теория графов: основные понятия и определения Угол. Прямой угол (с применением ИКТ)
Угол. Прямой угол (с применением ИКТ) презентации по математике
презентации по математике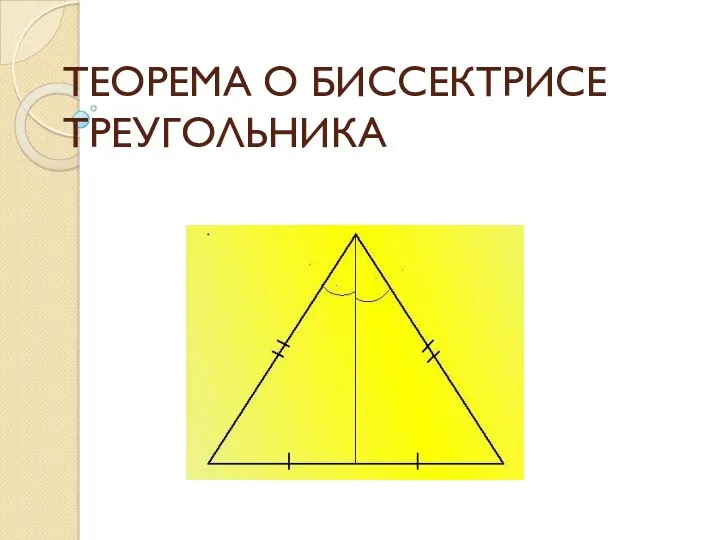 Теорема о биссектрисе треугольника
Теорема о биссектрисе треугольника Среднее арифметическое, размах и мода ряда чисел
Среднее арифметическое, размах и мода ряда чисел Вивчаємо арифметичні дії множення і ділення; табличне множення та ділення
Вивчаємо арифметичні дії множення і ділення; табличне множення та ділення Конспект урока математики во 2 классе. Умножение
Конспект урока математики во 2 классе. Умножение Функции и ее графики
Функции и ее графики Путешествие по математическим станциям
Путешествие по математическим станциям КУС по математике для 4 класса
КУС по математике для 4 класса Ученые математики
Ученые математики Понятие бесконечной интегральной суммы. Интеграл (11 класс)
Понятие бесконечной интегральной суммы. Интеграл (11 класс) Перпендикулярність прямої і площини
Перпендикулярність прямої і площини Основные формулы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей
Основные формулы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей Понятие площади многоугольника
Понятие площади многоугольника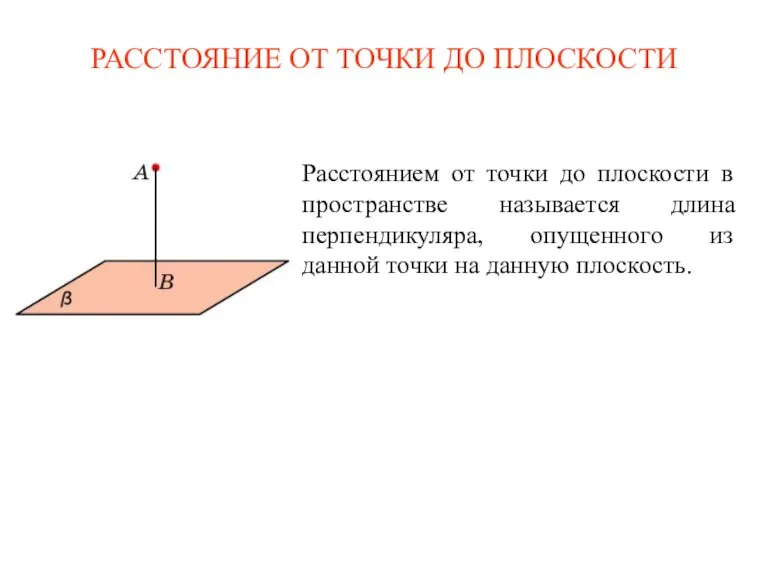 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Топқа бөлу
Топқа бөлу Педагогический опыт Развитие логического мышления и математических представлений у детей дошкольного возраста через развивающие игры
Педагогический опыт Развитие логического мышления и математических представлений у детей дошкольного возраста через развивающие игры Задачи на сравнение
Задачи на сравнение Упрощение выражений, 5 класс
Упрощение выражений, 5 класс