Содержание
- 2. ОГЛАВЛЕНИЕ
- 3. ЛЕКЦИИ
- 4. МАТРИЦЫ. ДЕЙСТВИЯ НАД МАТРИЦАМИ
- 5. Определение 1. Прямоугольная таблица из m строк и n столбцов, заполненная некоторыми математическими объектами, называется прямоугольной
- 6. Выражение называют размерностью матрицы. Матрица называется квадратной порядка n, если число ее строк равно числу столбцов
- 7. Квадратная матрица, элементы которой удовлетворяют условию: называется диагональной, т.е. диагональная матрица имеет вид: Диагональная матрица порядка
- 8. Определение 2. Две матрицы называются равными, если равны их размерности и равны их соответствующие элементы, т.е.
- 10. Например
- 11. Свойства операции сложения матриц Пусть A, B, C – матрицы одинаковой размерности: 1. A+ B= B+A
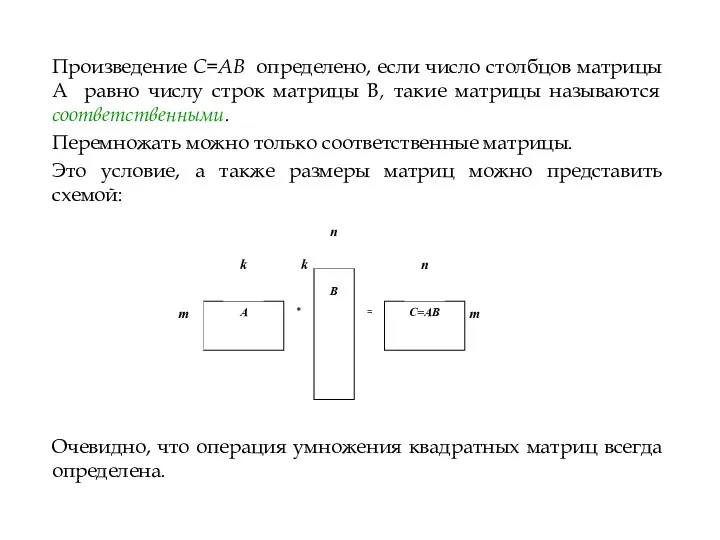
- 16. Произведение C=AB определено, если число столбцов матрицы A равно числу строк матрицы B, такие матрицы называются
- 18. Свойства умножения матриц 1. Коммутативный (переместительный) закон умножения матриц, вообще говоря, не выполняется, т.е. В частном
- 19. Определение 4. Если A – матрица размерности : то транспонированием этой матрицы называется такое преобразование, при
- 20. Определители. Свойства определителей. Понятие минора и алгебраического дополнения
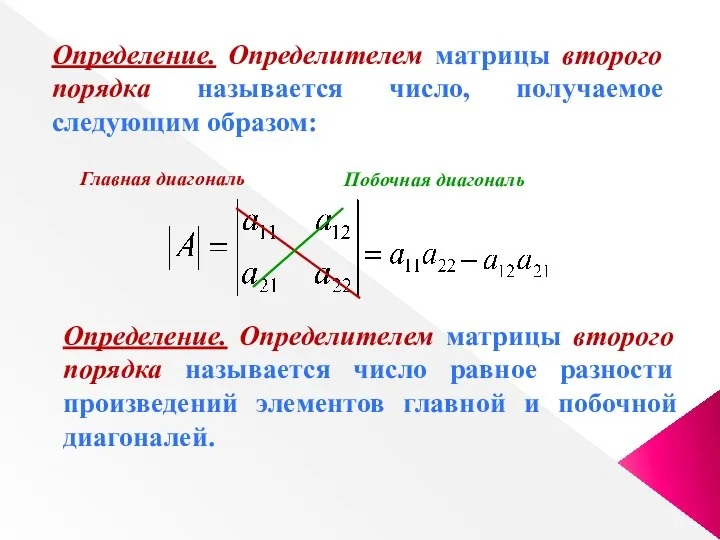
- 23. Побочная диагональ Главная диагональ
- 25. Определение. Определителем матрицы второго порядка называется число, получаемое следующим образом: Главная диагональ Побочная диагональ Определение. Определителем
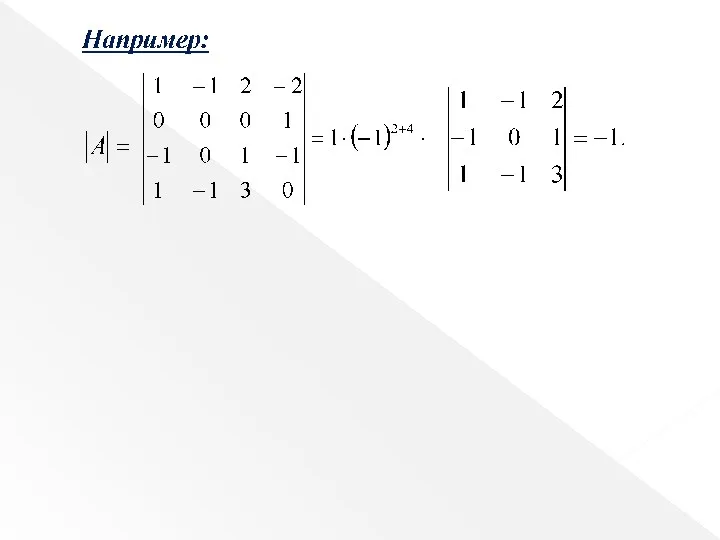
- 26. Например:
- 48. Обратная матрица
- 49. Матрица Вырожденная (особенная) Невырожденная (неособенная) определитель равен нулю Например: определитель отличен от нуля Например:
- 50. Теорема 1. Произведение матриц есть вырожденная матрица тогда и только тогда, когда хотя бы один из
- 51. Определение. Квадратная матрица В называется обратной по отношению к матрице А такого же размера, если АВ
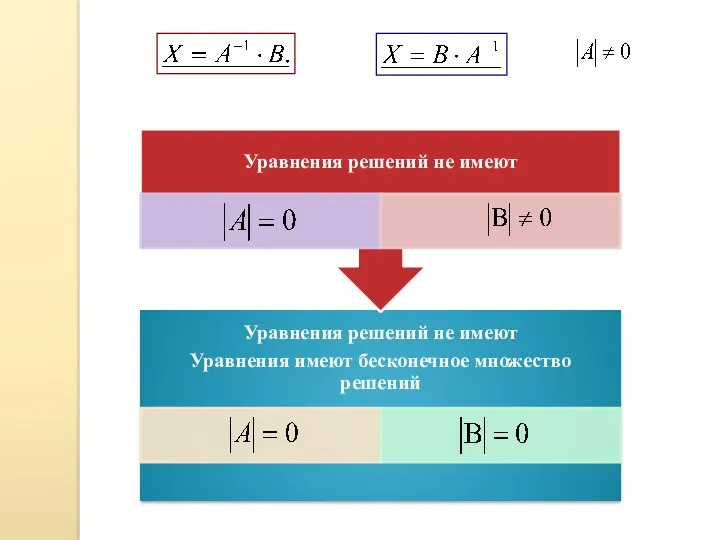
- 61. Системы линейных уравнений 1. Матричные уравнения
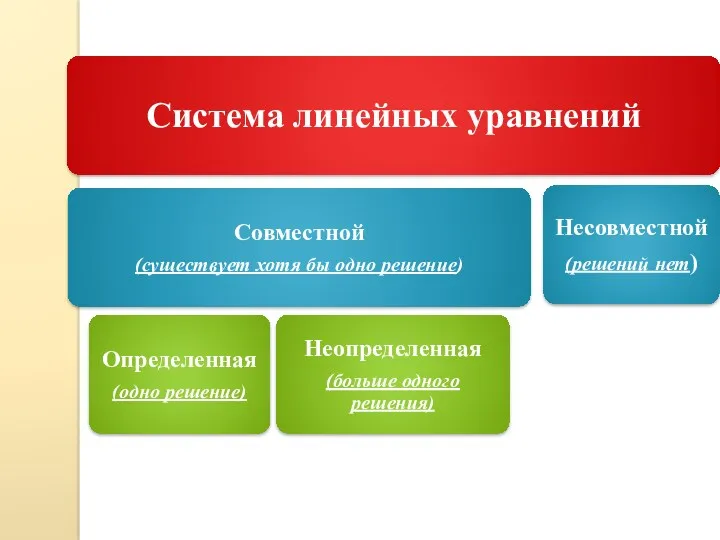
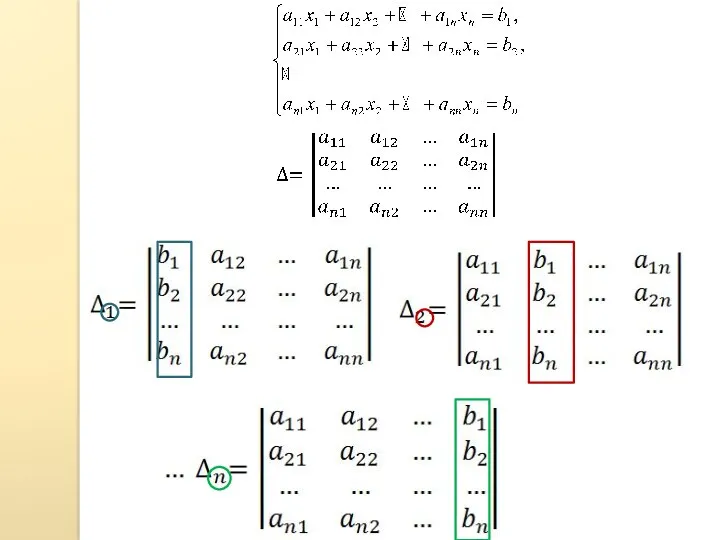
- 70. 2. Системы линейных уравнений 2. Квадратные системы линейных уравнений. Однородные системы. Правило Крамера
- 81. 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Метод Гаусса (метод последовательного исключения неизвестных)
- 82. Определение. Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, или равносильными,
- 83. СЛЕДУЮЩИЕ ПРЕОБРАЗОВАНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ БУДЕМ НАЗЫВАТЬ ЭЛЕМЕНТАРНЫМИ: перемена местами любых двух уравнений системы; умножение обеих
- 84. ТЕОРЕМА 1. Применение любого элементарного преобразования к системе линейных уравнений приводит к эквивалентной системе.
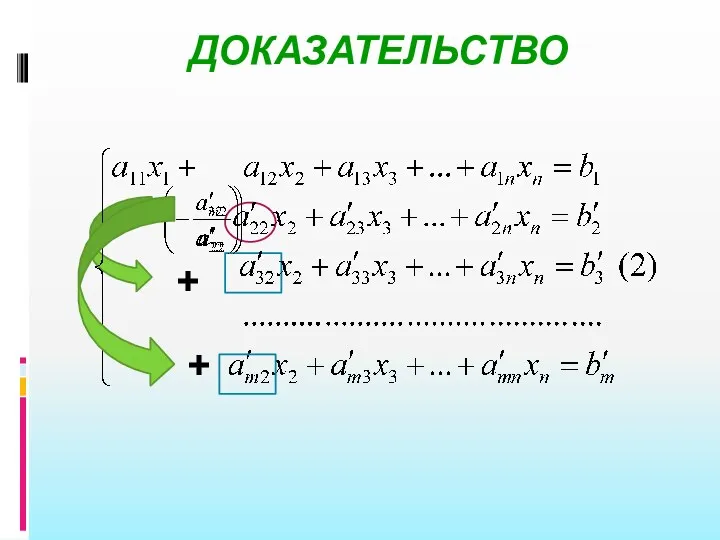
- 85. ДОКАЗАТЕЛЬСТВО + + +
- 87. ДОКАЗАТЕЛЬСТВО
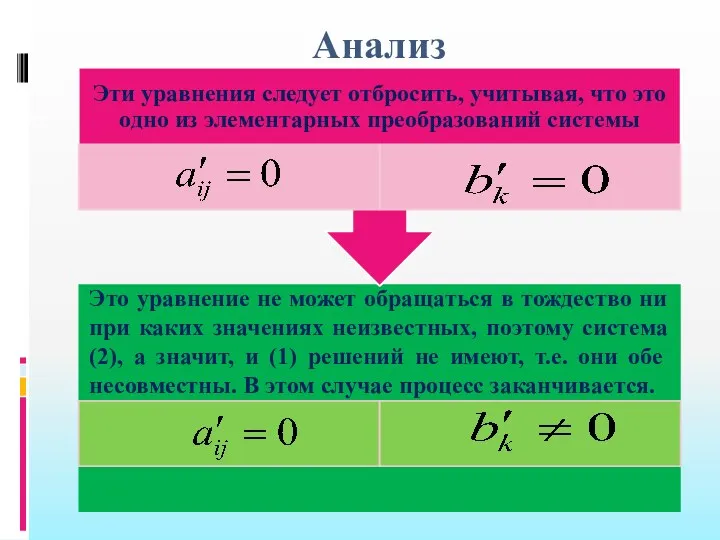
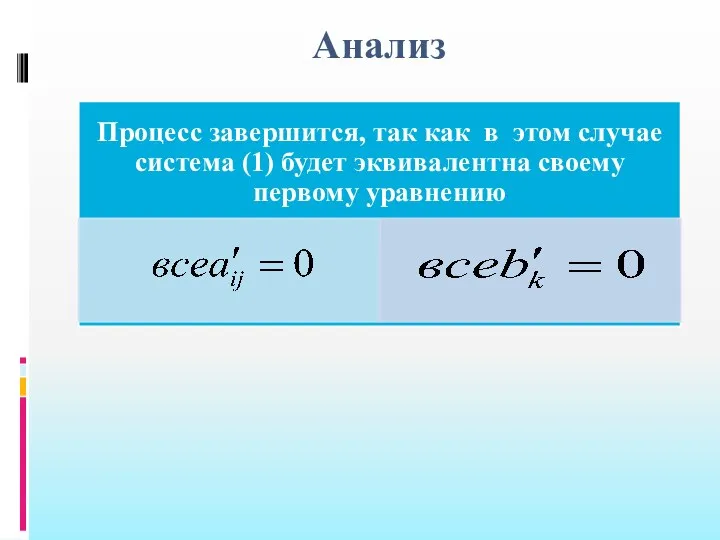
- 88. Анализ
- 89. Анализ
- 90. ДОКАЗАТЕЛЬСТВО + +
- 92. Доказательство k=n (определенная) k Треугольная Трапецеидальная
- 93. Решение для системы треугольного типа
- 94. Решение для системы трапецеидального типа
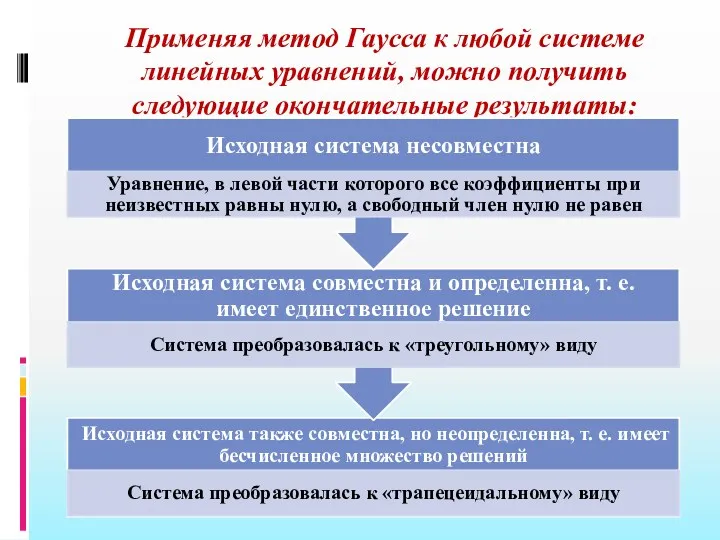
- 95. Применяя метод Гаусса к любой системе линейных уравнений, можно получить следующие окончательные результаты:
- 96. ТЕОРЕМА 2. Любую произвольную систему линейных уравнений с помощью элементарных преобразований можно привести к равносильной ей
- 97. РАСШИРЕННАЯ МАТРИЦА При практическом использовании метода Гаусса для решения систем линейных уравнений удобно проводить элементарные преобразования
- 98. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 99. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 100. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 101. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 102. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 103. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 104. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 105. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 106. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 107. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 108. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 109. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 110. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 111. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 112. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 113. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 114. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 115. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 116. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 117. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 118. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 119. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- 121. Скачать презентацию






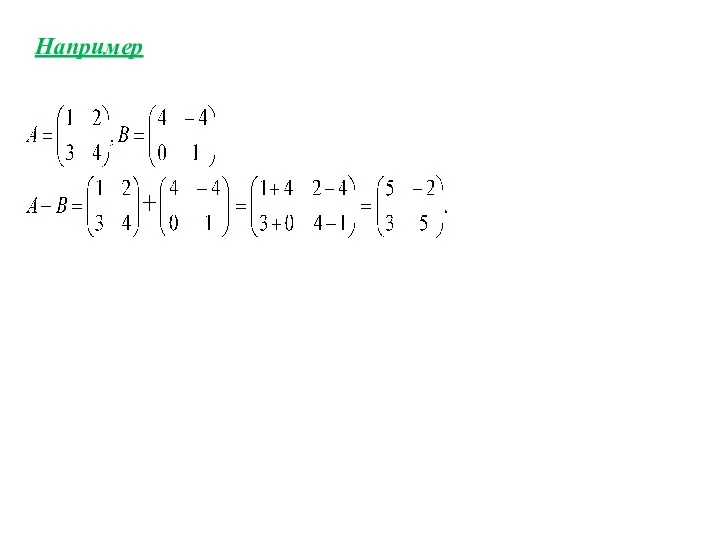































































































 Площадь треугольника. Решение одной задачи несколькими способами
Площадь треугольника. Решение одной задачи несколькими способами Критические точки функции. Точки экстремумов
Критические точки функции. Точки экстремумов Задачи на делимость
Задачи на делимость Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Дидактические игры по формированию элементарных математических представлений
Дидактические игры по формированию элементарных математических представлений Понятие логарифма, основные свойства логарифмов
Понятие логарифма, основные свойства логарифмов Чисельні методи. Лекція 2. Елементи теорії похибок
Чисельні методи. Лекція 2. Елементи теорії похибок Центральные и вписанные углы
Центральные и вписанные углы Площадь треугольника. Теоремы, следствия и задачи
Площадь треугольника. Теоремы, следствия и задачи 20230917_prilozhenie_k_masterskoy_prezentatsiya
20230917_prilozhenie_k_masterskoy_prezentatsiya Параллелепипед. Типы параллелепипедов
Параллелепипед. Типы параллелепипедов Мои уроки
Мои уроки Многогранники. Задачи
Многогранники. Задачи Шартты операция
Шартты операция Окружность и круг
Окружность и круг Равносильные уравнения
Равносильные уравнения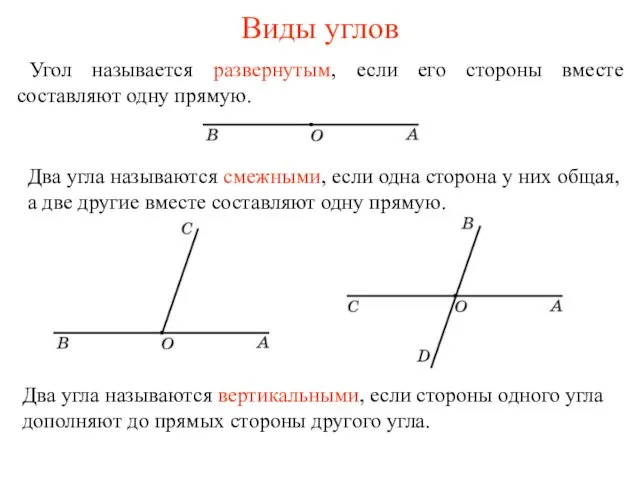 Виды углов
Виды углов Додавання та віднімання дробів з різними знаменниками
Додавання та віднімання дробів з різними знаменниками Разложение разности квадратов на множители. 7 класс
Разложение разности квадратов на множители. 7 класс УМК по предмету Счёт и конструирование и дидактический материал по данной теме, для подготовительного класса
УМК по предмету Счёт и конструирование и дидактический материал по данной теме, для подготовительного класса Решение задач по теме Правильный многоугольник
Решение задач по теме Правильный многоугольник Понятие и виды матриц
Понятие и виды матриц Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Презентация к уроку по математики по теме Вакыт, сәгать һәм минут
Презентация к уроку по математики по теме Вакыт, сәгать һәм минут Аксиомы планиметрии
Аксиомы планиметрии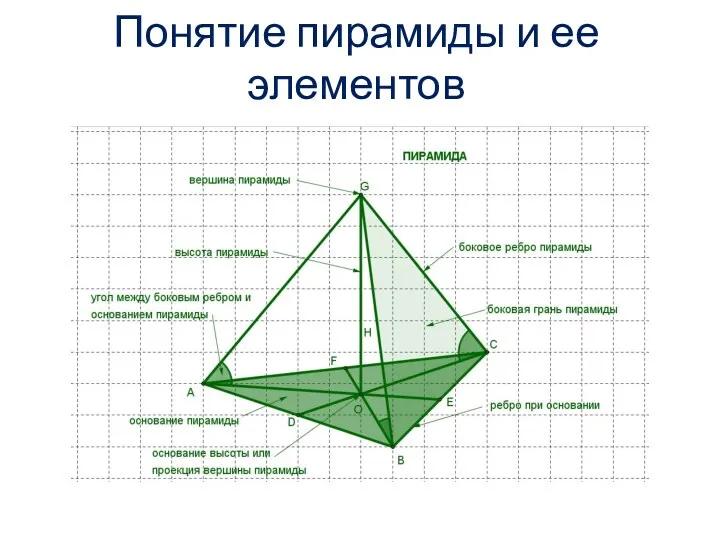 Понятие пирамиды и ее элементов. Правильная пирамида
Понятие пирамиды и ее элементов. Правильная пирамида Роль математики в современных профессиях
Роль математики в современных профессиях Текстовые задачи по математике
Текстовые задачи по математике