Содержание
- 2. Определим понятия: Модель Моделирование
- 3. Пример для мотивации применения моделирования
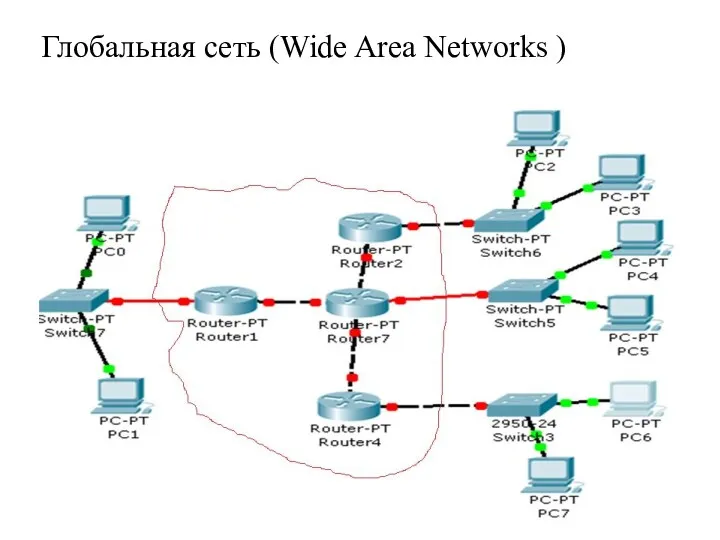
- 4. Глобальная сеть (Wide Area Networks )
- 5. Проблема: оценка показателей эффективности Для отдельного узла (маршрутизатора) сети Пропускная способность Среднее число пакетов в узле
- 6. Что такое модель? Модель (лат. modulus мера) это объект-заменитель системы-оригинала, отдельные свойства которого полностью или частично
- 7. Что такое моделирование?
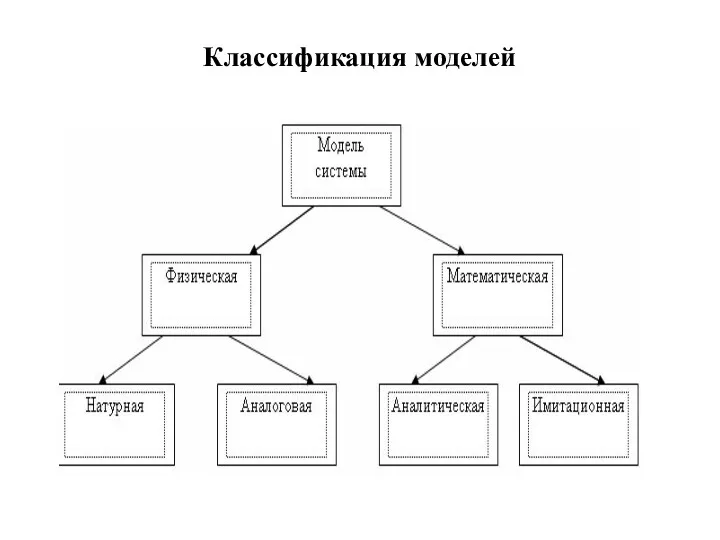
- 8. Классификация моделей
- 10. Математические модели (аналитические и имитационные)
- 11. Аналитическое моделирование 1. Теория Марковских процессов 2. Теория систем массового обслуживания (СМО) 3. Операционный анализ (частный
- 12. ЭЛЕМЕНТЫ ТЕОРИИ МАРКОВСКИХ ПРОЦЕССОВ
- 13. Definition and classification of random process Imagine an example of stochastic process from common stand. Assume
- 14. Let consider a function S(t) which values at some instants of time t0, t1, t2, …,
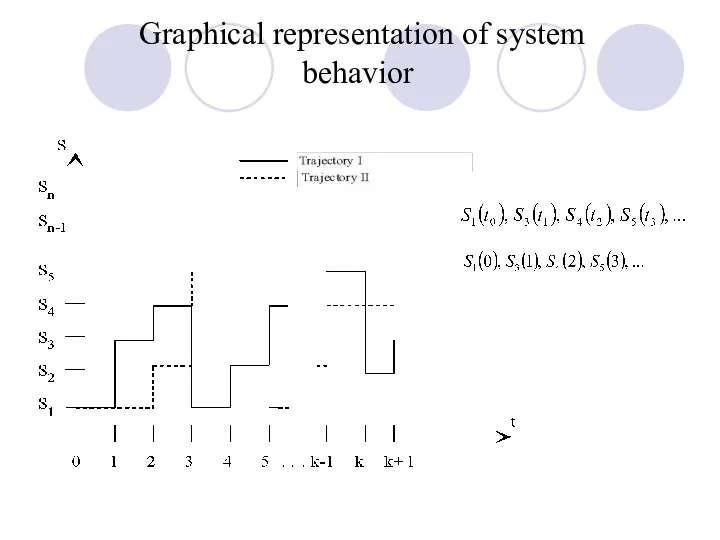
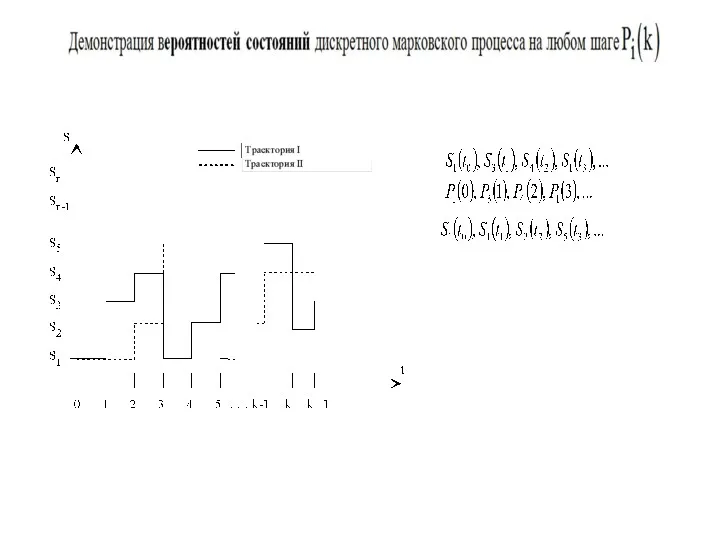
- 15. Graphical representation of system behavior
- 16. If the system S changes the states (passes from one state Si to another Sj) in
- 17. Stochastic process is a function S(t) which values are random values. In other words, stochastic process
- 18. Рассмотрим пример Процессор компьютера в любой заданный момент времени выполняет команды из: а) программы пользователя (состояние
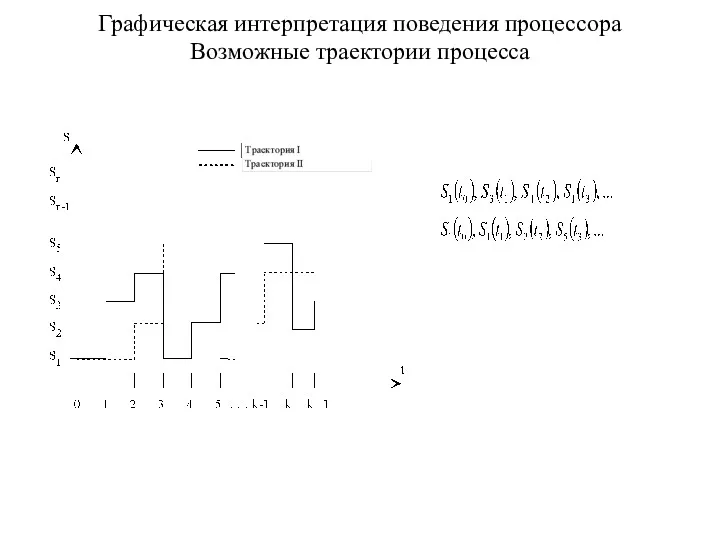
- 19. Графическая интерпретация поведения процессора Возможные траектории процесса
- 20. Определение случайных процессов Рассмотрим пример случайного процесса с общих позиций. Пусть имеется некоторая физическая система S,
- 21. Классификация состояний случайных процессов
- 22. Классификация случайных процессов по времени
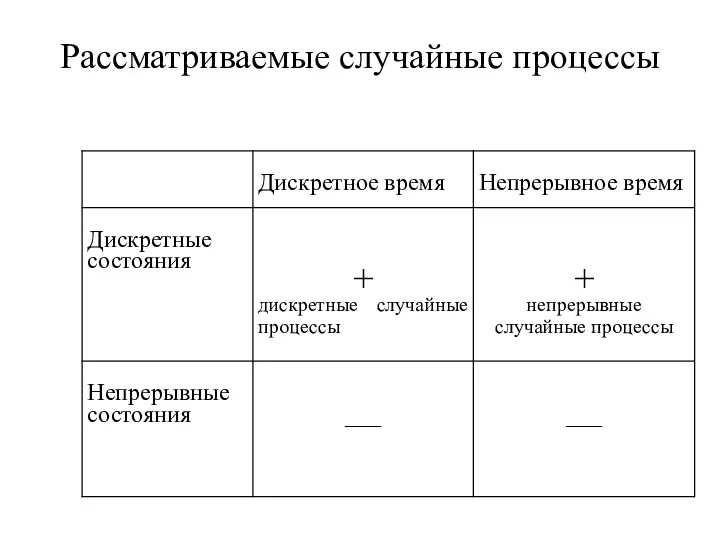
- 23. Рассматриваемые случайные процессы
- 24. Марковские процессы
- 25. Потоки событий. Простейший поток и его свойства
- 26. Потоки событий Потоком событий называется последовательность однородных событий, следующих одно за другим в некоторые моменты времени.
- 27. Свойства потоков
- 28. Потоки событий, обладающие некоторыми простыми свойствами (1)
- 29. Потоки событий, обладающие некоторыми простыми свойствами (2)
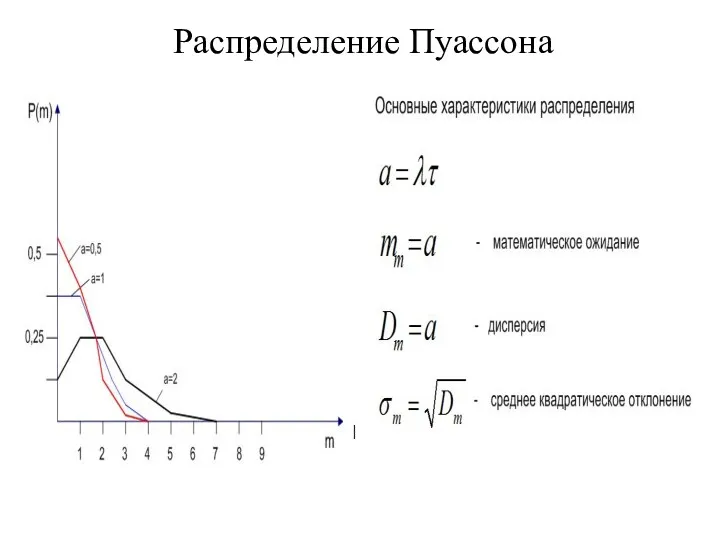
- 30. Распределение Пуассона . распределением Пуассона.
- 31. Распределение Пуассона
- 32. Простейший поток. Распределения интервала времени Т между соседними событиями
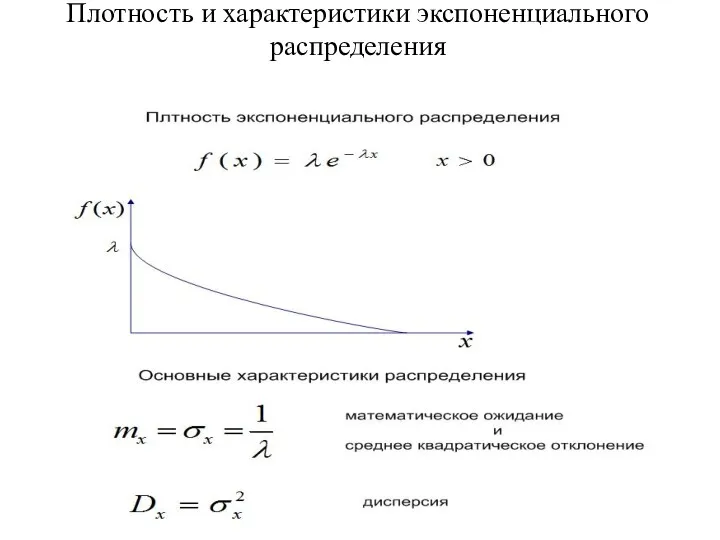
- 33. Плотность и характеристики экспоненциального распределения
- 34. Вероятность появления одного события на элементарном участке
- 35. Коэффициент вариации простейшего потока
- 36. Основные свойства простейшего потока
- 37. Дискретные марковские процессы Случайные процессы с дискретными состояниями и дискретным временем называются дискретными.
- 38. Формальные средства описания (модель) марковского процесса с дискретными состояниями (Граф состояний)
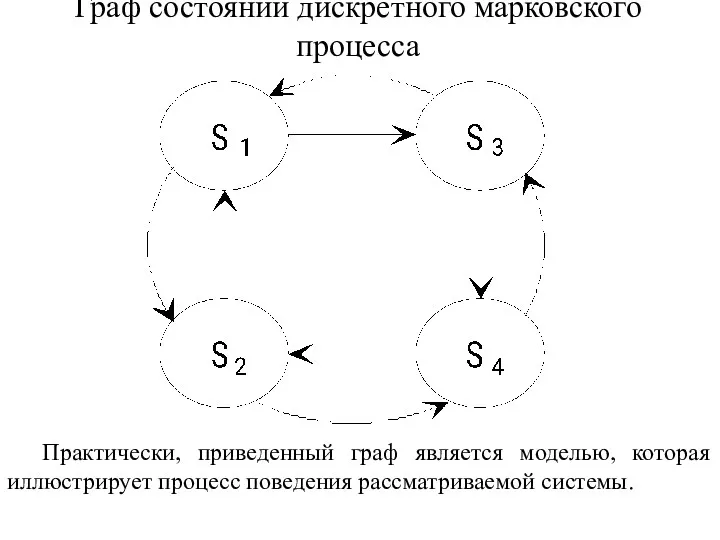
- 39. Граф состояний дискретного марковского процесса Практически, приведенный граф является моделью, которая иллюстрирует процесс поведения рассматриваемой системы.
- 40. Формальные средства описания марковского процесса с дискретными состояниями. (Марковская цепь)
- 41. Графическая интерпретация поведения процессора Возможные траектории процесса
- 42. Формальные средства описания марковского процесса с дискретными состояниями. Марковская цепь - продолжение
- 43. Переходная вероятность дискретного МП
- 44. Матрица переходных вероятностей неоднородного МП
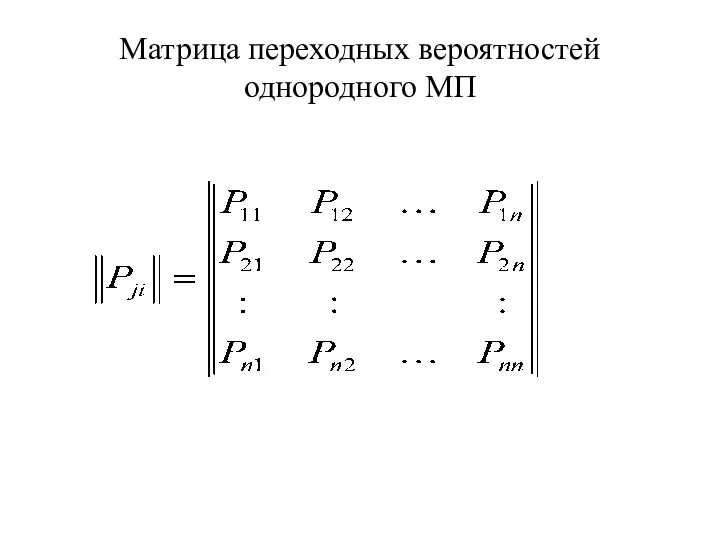
- 45. Матрица переходных вероятностей однородного МП
- 46. Свойства матрицы переходных вероятностей
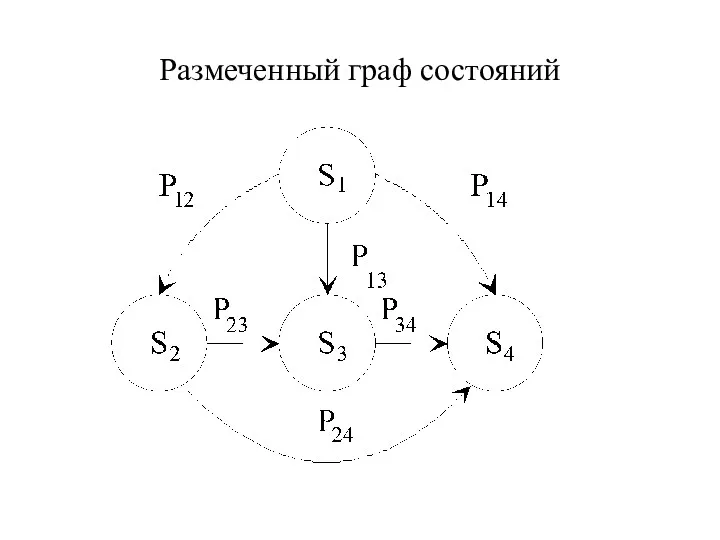
- 47. Размеченный граф состояний
- 48. Вычисление вероятностей состояний дискретного марковского процесса
- 50. Найдем Рi(1), или в общем виде для 1- го шага
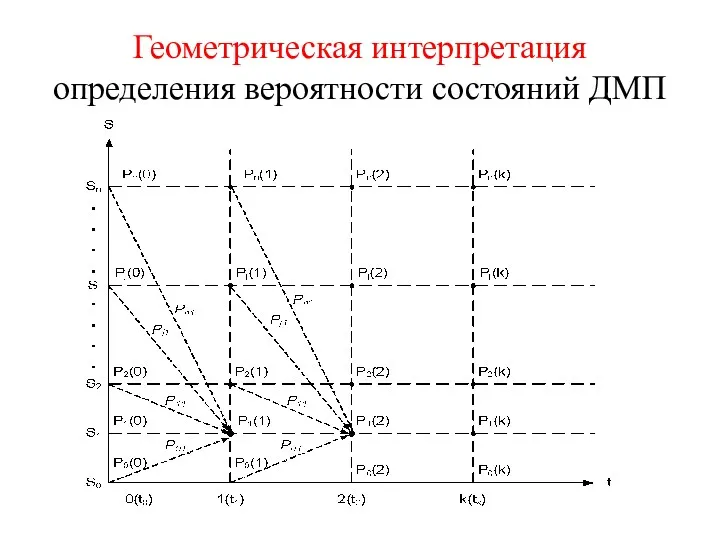
- 51. Геометрическая интерпретация определения вероятности состояний ДМП
- 52. Найдем Рi(2), или в общем виде для 2- го шага
- 53. Формулу вычисления вероятностей состояния на к-ом шаге для общего случая
- 54. Пример расчета ДМП
- 55. Формулы определения вероятностей состояний на 1-ом и 2-ом шаге
- 56. Пример расчета ДМП (результат)
- 57. Предельные вероятности состояний ДМП Основные определения Состояние называется возвратным, если вероятность возвращения марковского процесса в данное
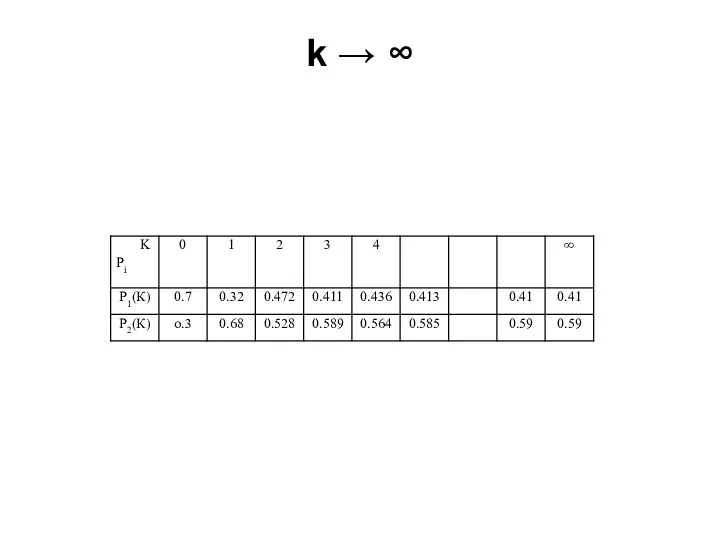
- 58. k → ∞
- 59. Теорема Маркова: Для эргодических марковских процессов справедлива теорема Маркова: если в системе протекает эргодический марковский процесс
- 60. Вычисление предельных вероятностей состояния ДМП Эта вероятность представляет собой долю времени пребывания системы в данном состоянии.
- 61. Предельных вероятности состояния Следовательно: P1 = 0.41 P2 = 0.59
- 62. Непрерывные марковские процессы
- 63. Непрерывные марковские процессы Т.к. для любого момента времени все состояния системы образуют полную группу несовместных событий,
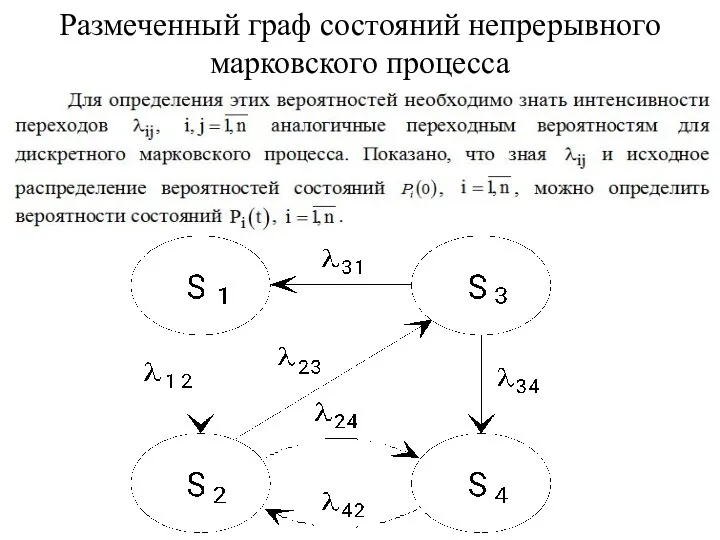
- 64. Размеченный граф состояний непрерывного марковского процесса
- 65. Уравнения Колмогорова для вероятностей состояний. Вычисление Pi(t)
- 66. Уравнения Колмогорова для вероятностей состояний (продолжение) Приведенная система уравнений имеет одно линейно зависимое.
- 67. Правило составления ДУК
- 68. Пример 1
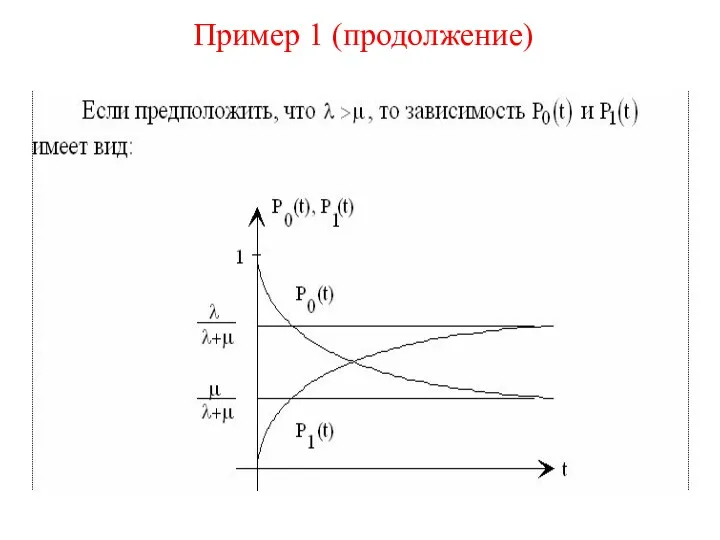
- 69. Пример 1 (продолжение)
- 70. Теорема Маркова для непрерывного марковского процесса. Эти вероятности представляют собой долю времени пребывания системы в соответствующем
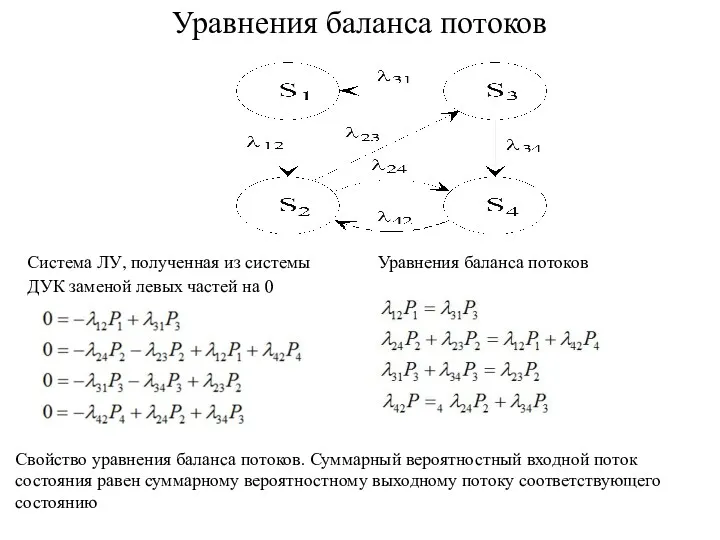
- 71. Уравнения баланса потоков Система ЛУ, полученная из системы ДУК заменой левых частей на 0 Уравнения баланса
- 72. Правило составления уравнений баланса потоков 1. Число уравнений равно числу состояний. 2. Левая часть каждого уравнения
- 73. Вычисление предельных вероятностей состояний Уравнения баланса потоков представляют собой систему линейных уравнений. Эта система имеет одно
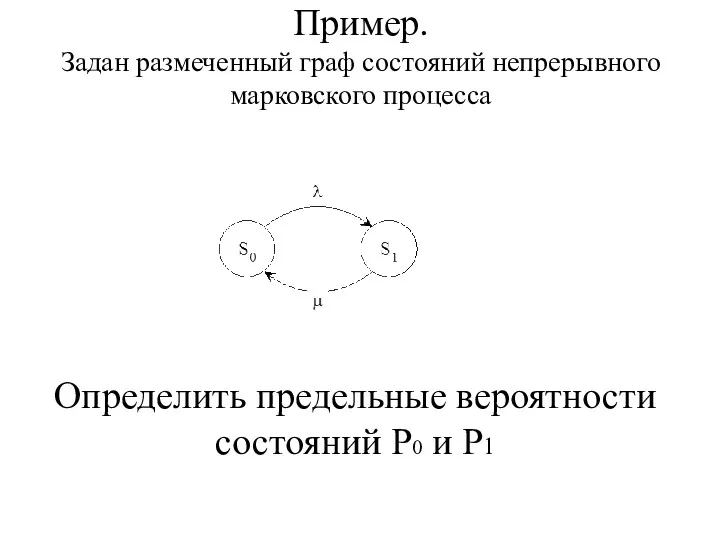
- 74. Пример. Задан размеченный граф состояний непрерывного марковского процесса Определить предельные вероятности состояний Р0 и Р1
- 75. Решение Уравнения баланса потоков: Нормировочное уравнение: Решение: отбросим первое уравнение
- 76. Процесс гибели и размножения
- 77. Уравнения баланса потоков для схемы гибели и размножения
- 79. Скачать презентацию




































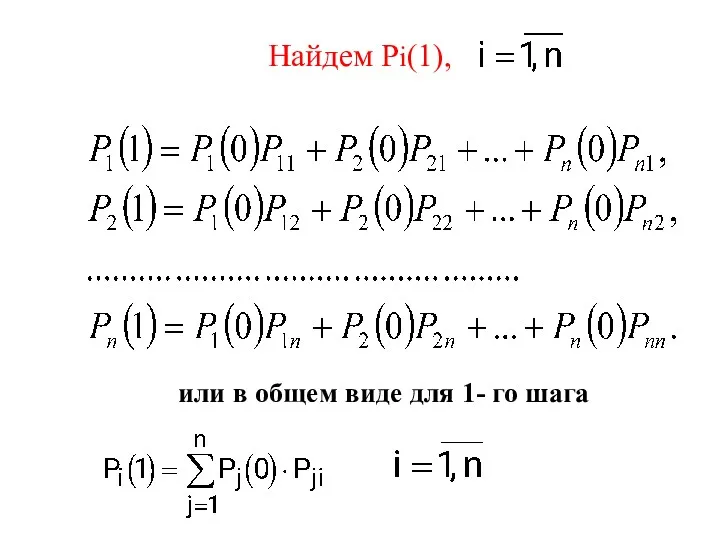
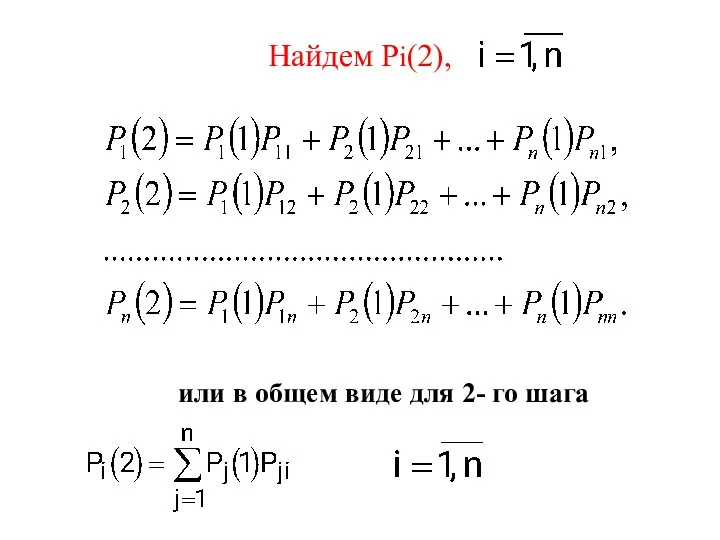




















 Review of Basic Concepts in Statistics
Review of Basic Concepts in Statistics Треугольник. Признаки равенства треугольников
Треугольник. Признаки равенства треугольников Перпендикуляр и наклонные. Расстояние от точки до плоскости
Перпендикуляр и наклонные. Расстояние от точки до плоскости Від’ємні числа, дії над ними
Від’ємні числа, дії над ними Сравнение дробей
Сравнение дробей Тест по теме: Призма. Часть 2. Вариант 1
Тест по теме: Призма. Часть 2. Вариант 1 Методы и системы поддержки принятия решений. Многокритериальный анализ решений: лексикографический метод, обобщенные критерии
Методы и системы поддержки принятия решений. Многокритериальный анализ решений: лексикографический метод, обобщенные критерии Графы. Основные понятия
Графы. Основные понятия Анализируем результаты ЕГЭ 15, готовимся к ЕГЭ 16
Анализируем результаты ЕГЭ 15, готовимся к ЕГЭ 16 Тригонометрические неравенства
Тригонометрические неравенства Признаки параллельности прямых. 7 класс
Признаки параллельности прямых. 7 класс презентация к уроку по математике Единицы времени. Год
презентация к уроку по математике Единицы времени. Год Графики тригонометрических функций
Графики тригонометрических функций Признаки делимости натуральных чисел. Практикум по решению задания №19 ЕГЭ (базовый уровень)
Признаки делимости натуральных чисел. Практикум по решению задания №19 ЕГЭ (базовый уровень) Презентация к открытому уроку по математике для 1 класса по теме:Секрет сложения.
Презентация к открытому уроку по математике для 1 класса по теме:Секрет сложения. Округление натуральных чисел
Округление натуральных чисел Быстрее. Выше. Сильнее. Тренажёр по математике
Быстрее. Выше. Сильнее. Тренажёр по математике Презентация для урока математики в 1 классе. Устный счет
Презентация для урока математики в 1 классе. Устный счет Урок математики(1класс)
Урок математики(1класс) Деление (математика, 3 класс, УМК Гармония)
Деление (математика, 3 класс, УМК Гармония) Решение задач на составление уравнений
Решение задач на составление уравнений Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Игра-тренажёр В гостях у ёжика (математика 1 класс)
Игра-тренажёр В гостях у ёжика (математика 1 класс) Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Теорема П'єра Ферма
Теорема П'єра Ферма Основы математического анализа
Основы математического анализа Решение планиметрических многовариантных задач
Решение планиметрических многовариантных задач Птицы из красной книги Башкортостана. Региональный компонент на уроках математики в начальной школе
Птицы из красной книги Башкортостана. Региональный компонент на уроках математики в начальной школе