Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их числовые характеристики презентация
Содержание
- 2. ЛЕКЦИЯ № 19 Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их
- 3. ЛИТЕРАТУРА Гмурман В.Е. Теория вероятностей и математическая статистика, Высшее образование, 2006, с. 50-63.
- 4. ЛИТЕРАТУРА Шолохович Ф.А. Высшая математика в кратком изложении. Баврин И.И. Высшая математика. Данко П.Е., Попов А.Г
- 5. УЧЕБНЫЕ ВОПРОСЫ 1.Теоремы о повторении опытов. Определение вероятности появления события не менее «m» раз и не
- 6. УЧЕБНЫй ВОПРОС Теоремы о повторении опытов. -Определение вероятности появления события не менее «m» раз и не
- 7. Теоремы о повторении опытов. Рассмотрим многократное повторение одного и того же испытания, в котором может либо
- 8. Формула Бернулли. Если вероятность появления события A в каждом испытании постоянна, то вероятность того, что событие
- 9. Пример. Вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что среди 10 деталей окажется более
- 11. Приближенные формулы в схеме Бернулли Локальная теорема Муавра-Лапласа Если вероятность р наступления события А в каждом
- 12. Пример. Вероятность поражения мишени стрелком равна р=0,8. Найти вероятность того, что при n= 100 выстрелах мишень
- 14. Интегральная теорема Муавра-Лапласа Если вероятность р наступления события А в каждом испытании постоянна и отлична от
- 15. где - функция Лапласа, её значения приведены в специальных таблицах; Ф(-х) = - Ф(х); Ф(х>5)=0,5.
- 16. Пример.
- 17. Формула Пуассона При большом числе n испытаний и сравнительно малой вероятности р наступления события А в
- 18. Пример. Вероятность угадывания 6 номеров в спортлото (6 из 49) равна 7,2· 10-8. При подсчете оказались
- 21. Определение вероятности появления события не менее «m» раз и не менее одного раза в «n» опытах.
- 22. событие А не наступит ни разу произойдет хотя бы раз ( не менее одного)
- 23. Отклонение относительной частоты от вероятности
- 24. УЧЕБНЫЙ ВОПРОС Теорема о полной вероятности, формула Байеса.
- 25. Теорема о полной вероятности. Пусть имеется группа событий В1, В2,..., Вn, обладающая следующими свойствами: 1) все
- 26. Пусть А - некоторое событие, которое может наступить лишь при появлении одного из событий Вi .
- 27. Пример. На трех станках изготавливаются одинаковые детали, причем на первом вырабатывается 50% всех деталей, на втором
- 28. Решение. Обозначим через А событие – наудачу взятая деталь соответствует стандарту. Возможны следующие предположения (гипотезы): В1-
- 29. Найдем вероятности этих гипотез. Поскольку на первом станке вырабатывается 50% всех деталей, то Р(В1) =0,5 ;
- 30. Искомую вероятность того, что наудачу взятая деталь соответствует стандарту, находим по формуле полной вероятности: Р(А)=Р(В1)·Р(А/В1)+Р(В2)·Р(А/В2)+ +Р(В3)·Р(А/В3)=
- 31. Пусть в результате проведения эксперимента появилось событие A. Если необходимо оценить вклад какого-либо события Вi в
- 32. Пример. Рассмотрим приведенную выше задачу о деталях, только изменим вопрос задачи. Пусть наудачу взятая деталь соответствует
- 33. Решение. По формуле Байеса Имеем
- 34. УЧЕБНЫЙ ВОПРОС Виды случайных величин и их числовые характеристики.
- 35. Под случайной величиной (С.В.) понимается числовая величина, которая в результате опыта может принять то или иное
- 36. Случайные величины Дискретные Непрерывные
- 37. Определение. Дискретной С.В. называют случайную величину, которая прини-мает только конечное или счетное число значений х1, х2,
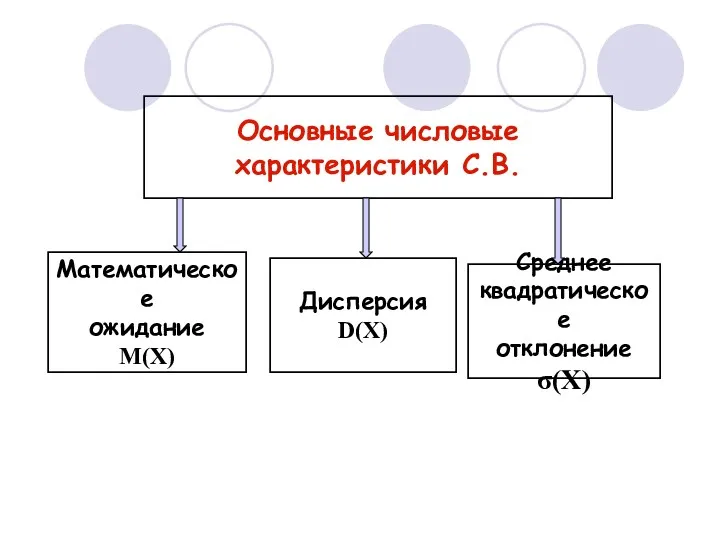
- 38. Основные числовые характеристики С.В. Математическое ожидание М(Х) Дисперсия D(Х) Среднее квадратическое отклонение σ(Х)
- 39. где : Математическое ожидание С.В. Х М(Х) называют средним значением С.В. Математическое ожидание показывает какое значение
- 40. Основные формулы, определяющие числовые характеристики С.В.
- 41. Функция распределения Универсальным законом распределения С.В. любого типа является функция распределения С.В.– вероятность того, что значение
- 42. Определение. Случайная величина Х называется непрерывной, если её функция распределения F(х) (интегральная функция распределения) непрерывна в
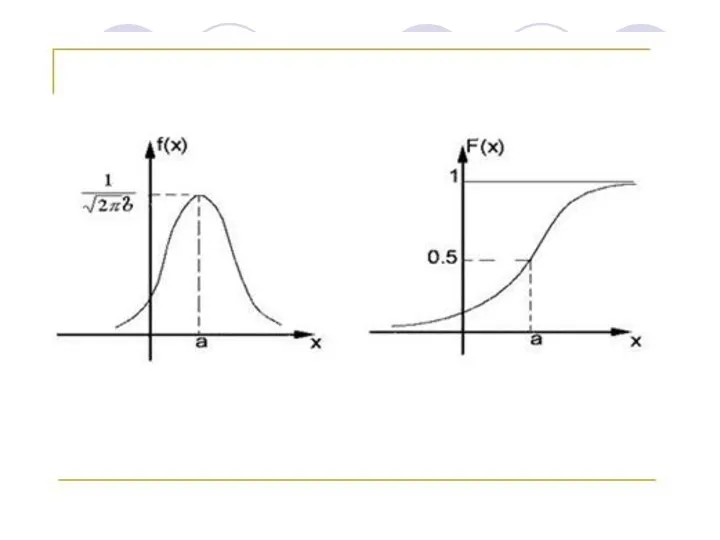
- 43. Нормальное распределение С. В. имеет нормальное распределение с параметрами а и σ, если её плотность распределения
- 46. Скачать презентацию








































 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Эконометрика. Обобщенный метод наименьших квадратов
Эконометрика. Обобщенный метод наименьших квадратов Треугольник. Четырехугольник. Окружность. Путешествие в геометрию
Треугольник. Четырехугольник. Окружность. Путешествие в геометрию Применение производной и первообразной показательной и логарифмической функции
Применение производной и первообразной показательной и логарифмической функции Неравенства
Неравенства Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке Величины 1 класс
Величины 1 класс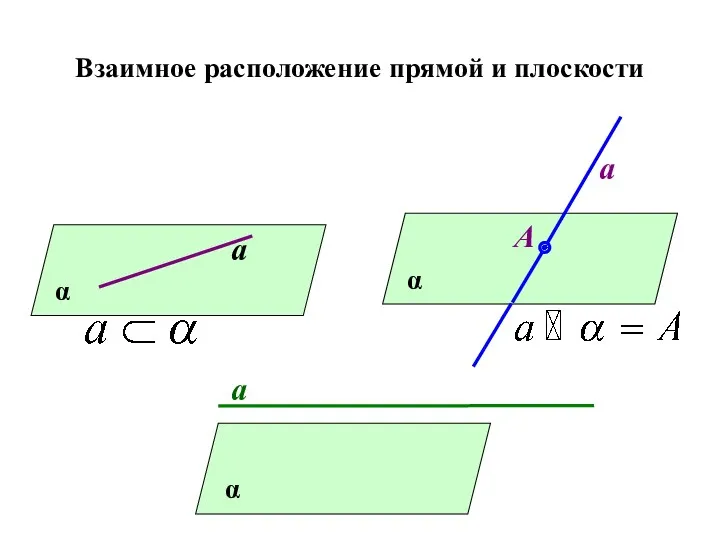 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости 20231001_mnogougolniki
20231001_mnogougolniki Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени
Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени Презентация Путешествие в страну дробей
Презентация Путешествие в страну дробей Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Как правильно писать цифры
Как правильно писать цифры Элементы теории вероятностей
Элементы теории вероятностей Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Тренировочная работа № 3
Тренировочная работа № 3 Площади. Равновеликие фигуры
Площади. Равновеликие фигуры Представление натуральных чисел на координатном луче
Представление натуральных чисел на координатном луче Скорость, время, расстояние. Математика, 4класс.
Скорость, время, расстояние. Математика, 4класс. ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов
ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Геометрические фигуры
Геометрические фигуры Математика. 1 класс. Урок 4. Признаки предметов
Математика. 1 класс. Урок 4. Признаки предметов Задача по финансовой математике
Задача по финансовой математике Правильный додекаэдр
Правильный додекаэдр Геометрические фигуры (презентация для подготовки)
Геометрические фигуры (презентация для подготовки) Вклад математиков в победу Великой Отечественной Войне
Вклад математиков в победу Великой Отечественной Войне Конспект урока математики (+ презентация). 4 класс
Конспект урока математики (+ презентация). 4 класс