Содержание
- 2. Основные понятия
- 3. Пусть имеется n+1 переменная x1, x2, ..., xn, y, которые связаны между собой так, что каждому
- 4. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x1,
- 5. Будем говорить, что задана функция двух переменных, если любой паре чисел (x;y) из некоторого множества D
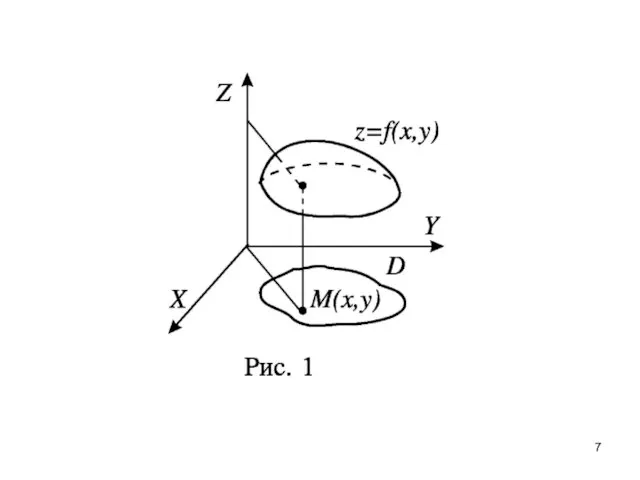
- 6. График функции двух переменных есть множество точек (x;y;f(x;y)), где (x;y)∈D. График представляет собой некоторую поверхность. Пример
- 8. Пусть δ ‑ некоторое положительное число. δ-окрестностью Vδ точки M0(x0;y0) называется множество всех точек, координаты (x
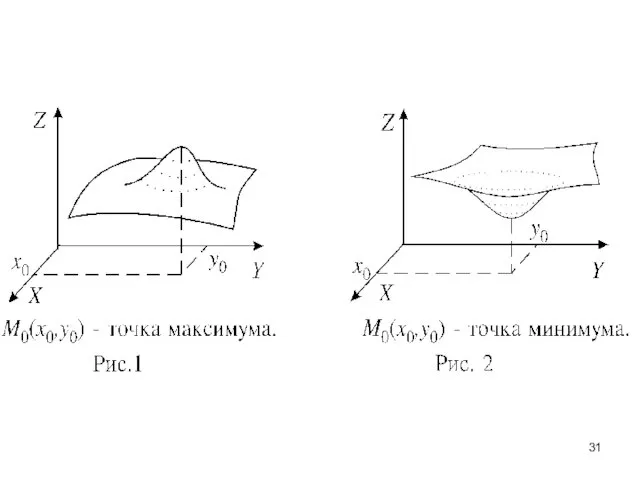
- 9. Точка M0(x0;y0) называется точкой минимума функции z = f(x;y), если существует такое положительное число δ, что
- 10. Точка M0(x0;y0) называется точкой максимума функции z = f(x;y), если существует такое положительное число δ, что
- 11. Число A называется пределом функции z = f(x;y) в точке M0(x0;y0): если для произвольного числа ε
- 12. Функция z = f(x;y) называется непрерывной в точке M0(x0;y0), если
- 13. Частные производные
- 14. Частной производной по x функции z = f(x;y) в точке M0(x0;y0) называется предел если этот предел
- 15. Совершенно аналогично можно определить частную производную по y функции z = f(x;y) в точке M0(x0;y0):
- 16. Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже
- 17. Если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности
- 18. Дифференциал функции двух переменных
- 19. Дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов.
- 20. Дифференцируемая в точке функция обязательно непрерывна в этой точке. Функция дифференцируема в точке, если обе частные
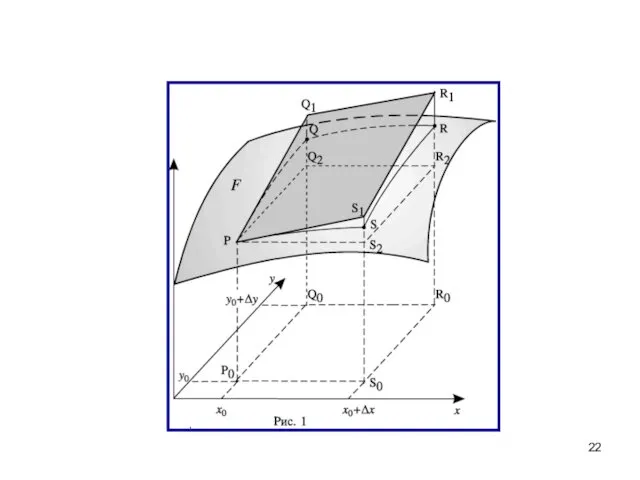
- 21. На рисунке 1 график функции z = f(x;y) представляет собой поверхность F. Длина отрезка Р0Р равна
- 23. Так как df(x0;y0) ≈ Δf(x0;y0), дифференциал df даёт приближенное значение приращения функции при малых значениях приращений
- 24. Производная по направлению
- 25. Производной функции z = f(x;y) в точке M0(x0;y0) по направлению называется число
- 26. Градиентом или вектором-градиентом функции f(x;y) в точке (x;y) ∈ G называется вектор, который задается формулой
- 27. Производная по направлению от функции z = f(x;y) в точке M0(x0;y0) достигает наибольшего значения, если это
- 28. Вектор-градиент функции в точке направлен в сторону наискорейшего возрастания функции в этой точке.
- 29. Экстремум функции двух переменных
- 30. Точка M0(x0;y0) является точкой максимума (минимума) функции z = f(x;y), если найдется такая окрестность точки M0,
- 32. Пусть zx′(x0,y0)=0 и zy′(x0,y0) = 0, а вторые частные производные функции z непрерывны в некоторой окрестности
- 33. Введем обозначения: A = zxx′′(x0;y0); B = zxy′′(x0;y0); C = zyy′′(x0;y0); D = AC - B2.
- 34. Тогда, если D Если D > 0, причем если A > 0, то в точке (x0;y0)
- 35. Метод наименьших квадратов
- 36. Пусть проводится n однородных испытаний или экспериментов, и результатом каждого испытания является пара чисел – значений
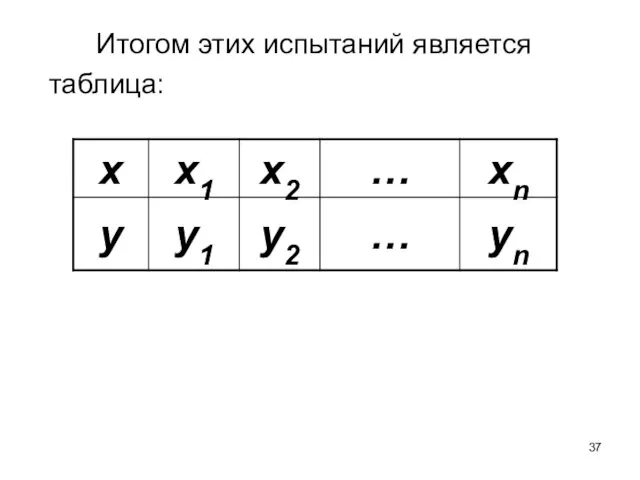
- 37. Итогом этих испытаний является таблица:
- 38. где каждому числу xi (величину x рассматриваем как независимый показатель или фактор) поставлено в соответствие число
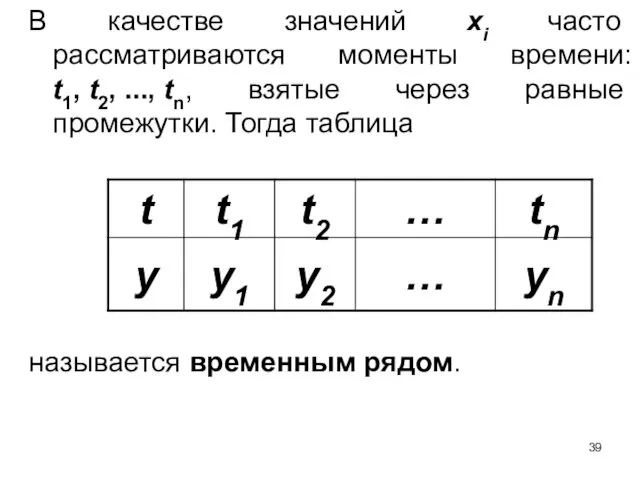
- 39. В качестве значений xi часто рассматриваются моменты времени: t1, t2, ..., tn, взятые через равные промежутки.
- 40. Пусть точки с координатами (xi,yi) группируются на плоскости вдоль некоторой прямой. Задача заключается в том, чтобы
- 41. Признаком наилучшей прямой считается минимум суммы квадратов отклонений фактических значений y, полученных из таблицы, от вычисленных
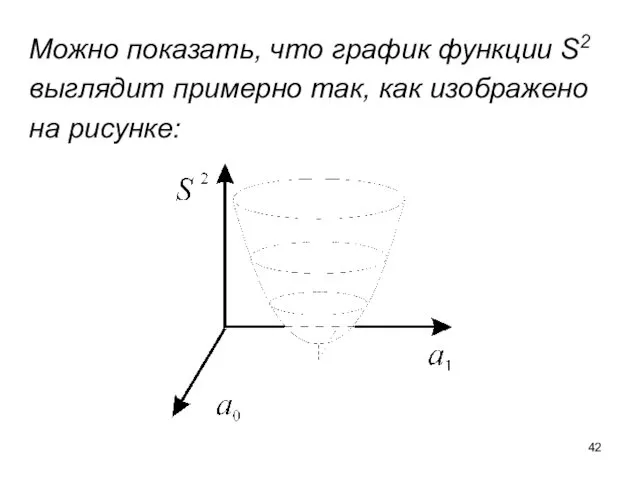
- 42. Можно показать, что график функции S2 выглядит примерно так, как изображено на рисунке:
- 43. Точку минимума можно искать, используя лишь необходимые условия экстремума: (2) (3)
- 44. Уравнения (2) и (3) можно преобразовать: Получилась так называемая система нормальных уравнений относительно неизвестных величин a0
- 46. Скачать презентацию









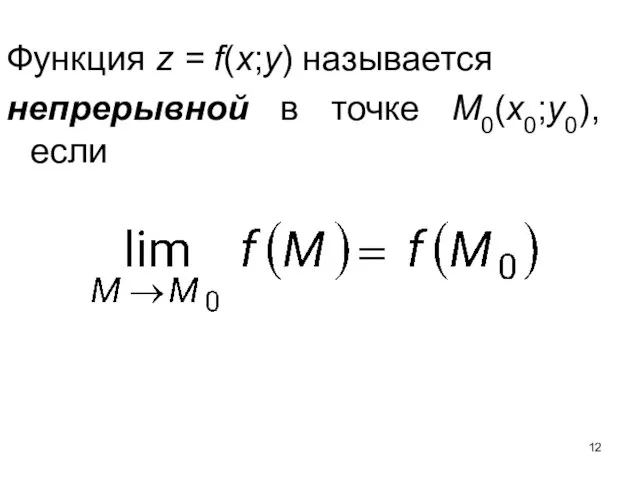



























 Готовимся к ЕГЭ. Математика
Готовимся к ЕГЭ. Математика Сложение и вычитание многочленов
Сложение и вычитание многочленов История возникновения десятичных дробей
История возникновения десятичных дробей Хордовая вышивка
Хордовая вышивка Квадрат суммы и квадрат разности
Квадрат суммы и квадрат разности Методики выполнения измерений, как основа метрологического обеспечения
Методики выполнения измерений, как основа метрологического обеспечения урок математики Закрепление знаний о геометрических фигурах
урок математики Закрепление знаний о геометрических фигурах Признаки параллельных прямых. 7 класс
Признаки параллельных прямых. 7 класс Презентация к уроку математики:Задачи на увеличение (уменьшение) на несколько единиц .
Презентация к уроку математики:Задачи на увеличение (уменьшение) на несколько единиц . Задачи на готовых чертежах. Квадрат
Задачи на готовых чертежах. Квадрат Элементы теории алгоритмов
Элементы теории алгоритмов Розв’язуємо складені задачі
Розв’язуємо складені задачі Числа правят миром
Числа правят миром Сложение и вычитание дробей
Сложение и вычитание дробей Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Описанная окружность. Треугольник, вписанный в окружность. Касательная к окружности. Окружность, вписанная в треугольник
Описанная окружность. Треугольник, вписанный в окружность. Касательная к окружности. Окружность, вписанная в треугольник Прямоугольник. 8 класс
Прямоугольник. 8 класс Математика. 1 класс
Математика. 1 класс Трикутники в навколишньому світі
Трикутники в навколишньому світі Линейные уравнения. 7 класс
Линейные уравнения. 7 класс Математический поезд.
Математический поезд. Возникновение и развитие алгебры
Возникновение и развитие алгебры Верные и неверные предложения
Верные и неверные предложения Подготовка к ЕГЭ по математике. Решение заданий В9
Подготовка к ЕГЭ по математике. Решение заданий В9 Параллельные плоскости
Параллельные плоскости Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Преобразования графиков функций
Преобразования графиков функций Вычисление первообразных функции
Вычисление первообразных функции