Содержание
- 2. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
- 3. Системы любого числа линейных алгебраических уравнений где a11,…,amn, b1,…,bm некоторые числа. Если b1=0,….,bm=0, то система называется
- 4. Системы любого числа линейных алгебраических уравнений где вектор–столбец неизвестных, вектор–столбец свободных членов,
- 5. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
- 6. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
- 7. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
- 8. Системы любого числа линейных алгебраических уравнений Т е о р е м а 2. Решение системы
- 9. Системы любого числа линейных алгебраических уравнений Метод Гаусса Для решения системы (2) с матрицей А размерности
- 10. Системы любого числа линейных алгебраических уравнений - система совместна, - базисными неизвестными объявить те, номера которых
- 11. Системы любого числа линейных алгебраических уравнений 3) Привести ступенчатую матрицу, полученную при выполнении шага 1), к
- 12. Системы любого числа линейных алгебраических уравнений З а м е ч а н и е 2.
- 13. ПРИМЕРЫ П р и м е р 1. Для системы: указать матрицу системы А и столбец
- 14. ПРИМЕРЫ Тогда матрица А рассматриваемой системы составляется из числовых коэффициентов, стоящих в системе при неизвестных:
- 15. ПРИМЕРЫ Столбец составляется из свободных членов системы: Поэтому систему можно переписать в векторной форме: О т
- 16. ПРИМЕРЫ П р и м е р 2. Исследовать на совместность систему: Р е ш е
- 17. ПРИМЕРЫ Выполним шаг 1) метода Гаусса: Следовательно: и О т в е т: система несовместна.
- 18. ПРИМЕРЫ П р и м е р 3. Решить систему: Р е ш е н и
- 19. ПРИМЕРЫ
- 20. ПРИМЕРЫ О т в е т:
- 21. ПРИМЕРЫ П р и м е р 4. Исследовать на совместность и решить систему:
- 22. ПРИМЕРЫ Р е ш е н и е. Воспользуемся методом Гаусса: составим матрицу А рассматриваемой системы,
- 23. ПРИМЕРЫ
- 24. ПРИМЕРЫ
- 26. Скачать презентацию
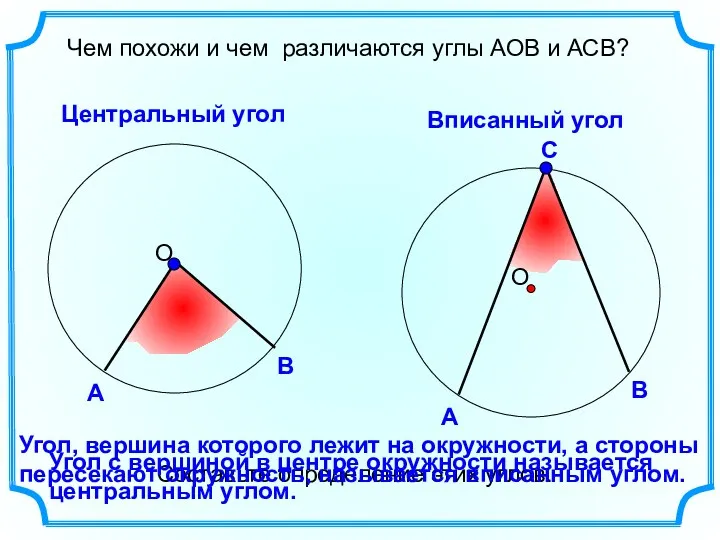 Вписанные углы
Вписанные углы Расчет пластин
Расчет пластин Минимизация переключательных функций по картам Карно
Минимизация переключательных функций по картам Карно Синус, косинус и тангенс
Синус, косинус и тангенс Два замечательных предела
Два замечательных предела Презентация к уроку математики в 1 классе по теме Решение простых задач на разностное сравнение, разбиение на группы, составление выражений.
Презентация к уроку математики в 1 классе по теме Решение простых задач на разностное сравнение, разбиение на группы, составление выражений. Нахождение числа по его дроби. 6 класс
Нахождение числа по его дроби. 6 класс Презентация Система работы по использованию блоков Дьенеша в работе по ФЭМП
Презентация Система работы по использованию блоков Дьенеша в работе по ФЭМП Геометрические тела, площади их поверхностей и объемы
Геометрические тела, площади их поверхностей и объемы Взаимно простые числа. Признак делимости на пр-е. НОК
Взаимно простые числа. Признак делимости на пр-е. НОК Аксиома параллельных прямых
Аксиома параллельных прямых Интегрирование простых функций
Интегрирование простых функций Десятичные дроби произвольного знака
Десятичные дроби произвольного знака Трёхмерное пространство. Координатная плоскость
Трёхмерное пространство. Координатная плоскость Презентация по теме: Поездка на Олимпийские игры
Презентация по теме: Поездка на Олимпийские игры Виды треугольников
Виды треугольников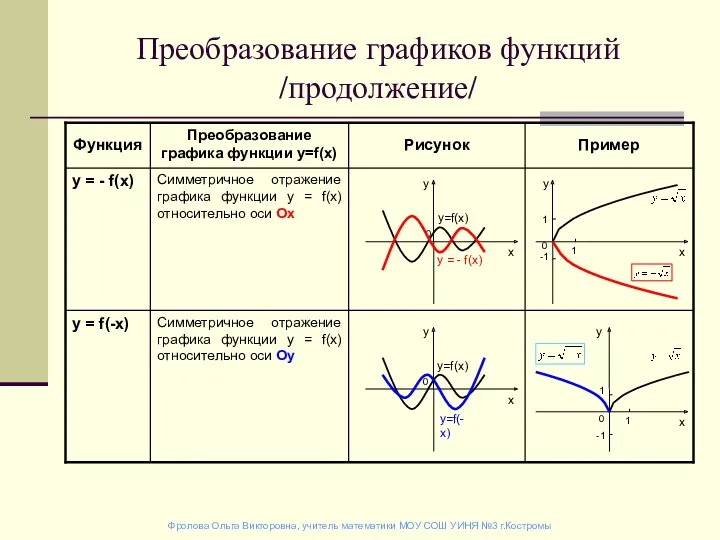 Преобразование графиков функций (продолжение)
Преобразование графиков функций (продолжение) Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Презентация по математическому развитию по программе Детство
Презентация по математическому развитию по программе Детство Подготовка к контрольной работе по теме Треугольники
Подготовка к контрольной работе по теме Треугольники Диаметр окружности. Круг. К уроку №59. Математика. 3 класс
Диаметр окружности. Круг. К уроку №59. Математика. 3 класс Көбейтудің қосуға қарағандағы үлестірімділік қасиеті
Көбейтудің қосуға қарағандағы үлестірімділік қасиеті Математические модели теории надежности
Математические модели теории надежности Интервальные ряды
Интервальные ряды Угол. Прямой угол
Угол. Прямой угол Число і цифра 9. (1 клас)
Число і цифра 9. (1 клас) Сравнение чисел
Сравнение чисел Сравнение обыкновенных дробей. Как называется число, записанное под дробной чертой?
Сравнение обыкновенных дробей. Как называется число, записанное под дробной чертой?