Содержание
- 2. Геометрические построения – решение геометрических задач на построение геометрических фигур с помощью различных инструментов.
- 3. Древнегреческие математики считали истинно геометрическими лишь построения, производимые циркулем и линейкой. При этом они рассматривали линейку
- 4. Ограничений средств геометрических построений только циркулем и линейкой придерживался Евклид, хотя в «Началах» названия циркуля и
- 5. Леонардо да Винчи рассматривал построения с помощью линейки и циркуля постоянного размаха Леонардо да Винчи (1452-1519)
- 6. Укажите инструменты, используемые при классических построениях
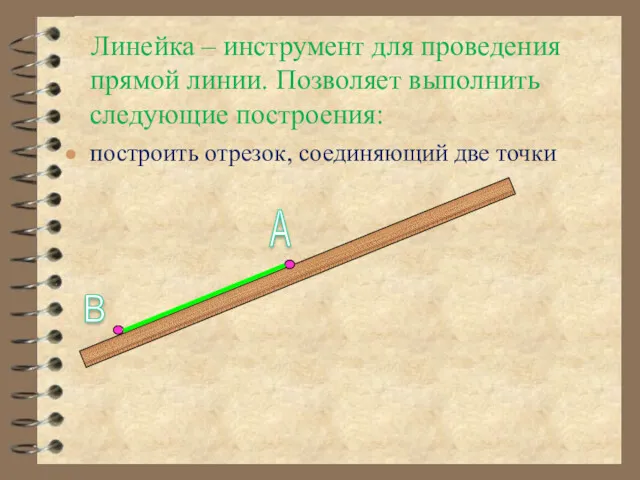
- 7. Линейка – инструмент для проведения прямой линии. Позволяет выполнить следующие построения: построить отрезок, соединяющий две точки
- 8. построить прямую, проходящую через две точки В А
- 9. построить луч, исходящий из точки и проходящий через другую точку В А
- 10. Циркуль – инструмент для вычерчивания окружностей и их дуг. Позволяет выполнить следующие построения: построить окружность с
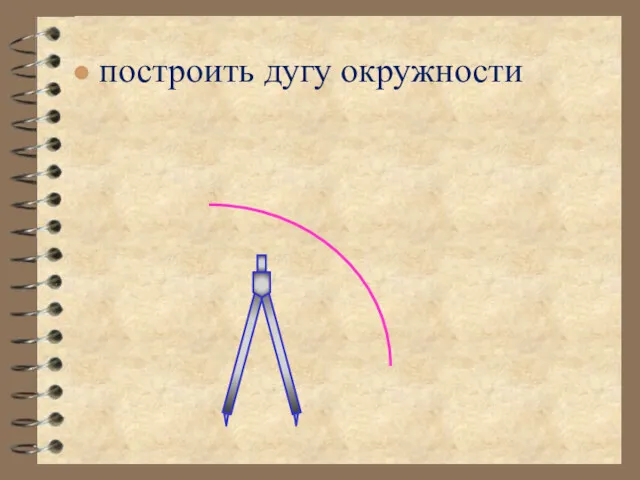
- 11. построить дугу окружности
- 12. Условные обозначения ∠ - знак угла окр(О;г) - окружность с центром в точке О и радиусом
- 13. Задача 1 На данном луче от его начала отложить отрезок, равный данному Дано: Луч h, О-
- 14. Задача 2 Построить середину данного отрезка Дано: АВ-отрезок А Построить: О∈АВ ОА=ОВ О: Построение: 1. окр(А
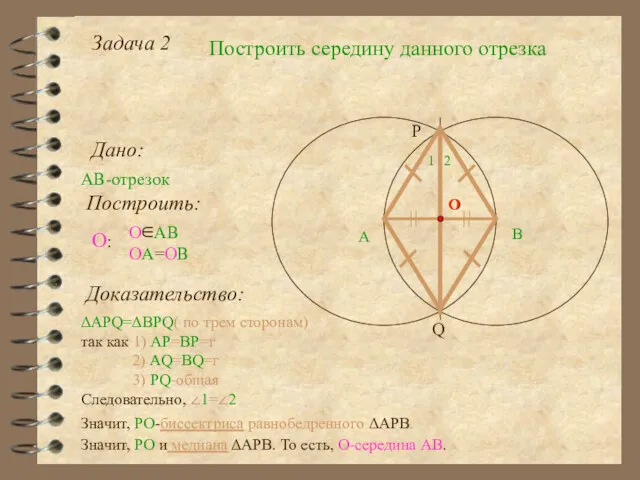
- 15. Задача 2 Построить середину данного отрезка Дано: АВ-отрезок А Построить: О∈АВ ОА=ОВ О: P Q О
- 16. Задача 3 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
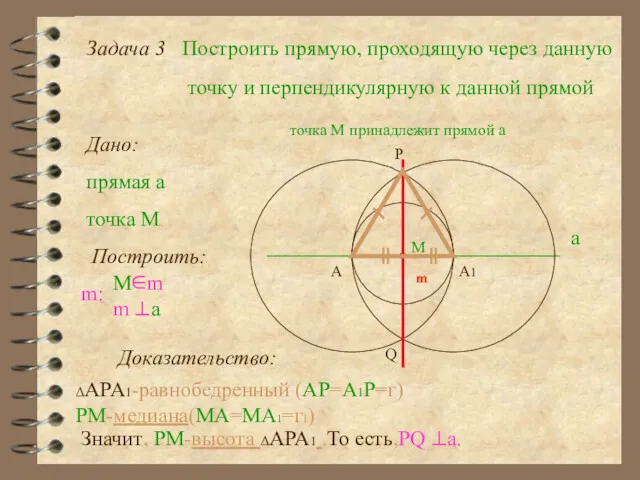
- 17. Задача 3 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
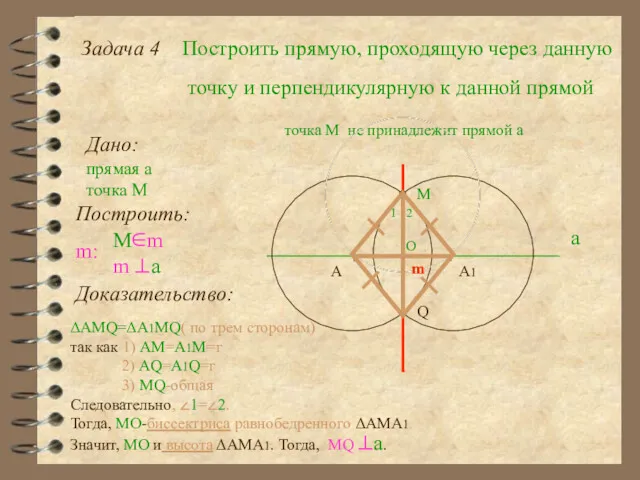
- 18. Задача 4 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
- 19. Задача 4 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
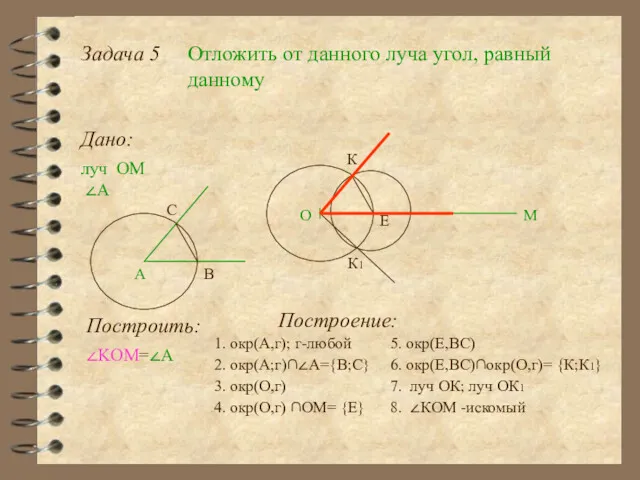
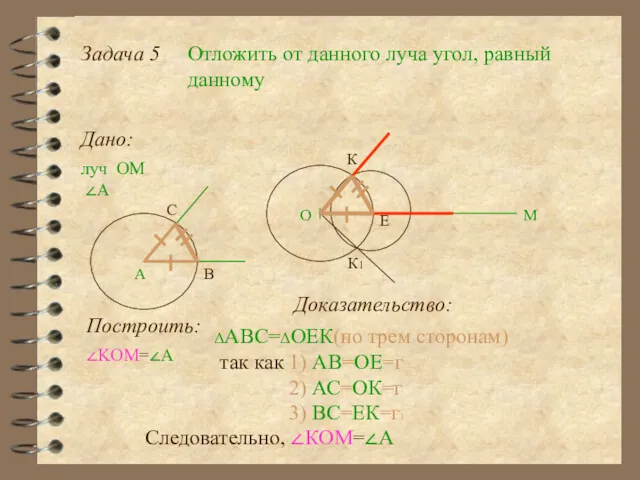
- 20. Задача 5 Отложить от данного луча угол, равный данному Дано: луч ОМ О М ∠А А
- 21. Задача 5 Отложить от данного луча угол, равный данному Дано: луч ОМ О М ∠А А
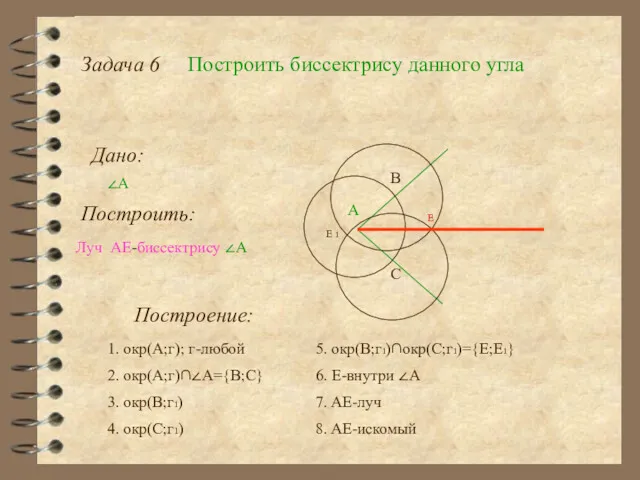
- 22. Задача 6 Построить биссектрису данного угла Дано: ∠А Построить: Построение: А 1. окр(А;г); г-любой Луч AE-биссектрису
- 23. Задача 6 Построить биссектрису данного угла Дано: ∠А Построить: А Луч AE-биссектрису ∠А C B E
- 24. Древнегреческие математики достигли большого искусства в геометрических построениях с помощью циркуля и линейки. Однако три задачи
- 25. Великие задачи древности Квадратура круга Трисекция угла Удвоение куба
- 26. В конце концов было доказано, что эти задачи невозможно решить, пользуясь только циркулем и линейкой. Но
- 28. Скачать презентацию

















 Векторы. Тест. (Вариант 2)
Векторы. Тест. (Вариант 2) Правописание числительных – орфография на уроках математики (Интегрированный урок: русский язык + математика)
Правописание числительных – орфография на уроках математики (Интегрированный урок: русский язык + математика) Умножение десятичных дробей. Свойства умножения
Умножение десятичных дробей. Свойства умножения Решение тригонометрических уравнений
Решение тригонометрических уравнений Чётные и нечётные функции
Чётные и нечётные функции Осевая и центральная симметрия. Симметричность точек относительно прямой
Осевая и центральная симметрия. Симметричность точек относительно прямой Урок – космическое путешествие по математике в 1 классе на тему: Решение примеров вида 15-
Урок – космическое путешествие по математике в 1 классе на тему: Решение примеров вида 15- Цифра и число 9
Цифра и число 9 Элементы математической статистики, комбинаторики и теории вероятностей. Формула бинома Ньютона
Элементы математической статистики, комбинаторики и теории вероятностей. Формула бинома Ньютона Треугольник. Тест. Задания в группах
Треугольник. Тест. Задания в группах Системы линейных неравенств с одним неизвестным. 9 класс
Системы линейных неравенств с одним неизвестным. 9 класс Урок по математике в 1 классе. Части величин. Школа 2000 (автор учебника Л.Г. Петерсон)
Урок по математике в 1 классе. Части величин. Школа 2000 (автор учебника Л.Г. Петерсон) Мир фракталов. Творческий проект
Мир фракталов. Творческий проект Перпендикулярные прямые
Перпендикулярные прямые открытый урок по математике на тему Площадь фигур 4 класс
открытый урок по математике на тему Площадь фигур 4 класс Число 10
Число 10 Метрологическое обеспечение производства
Метрологическое обеспечение производства презентация к уроку математики Цифра 1 и чичла 1, 2, 3, 4, 5,
презентация к уроку математики Цифра 1 и чичла 1, 2, 3, 4, 5, Рациональные числа
Рациональные числа Второй и третий признаки равенства треугольников. 7 класс
Второй и третий признаки равенства треугольников. 7 класс Числовые ряды. Общие определения и свойства. Сходимость рядов. Признаки сходимости. (Семинар 25)
Числовые ряды. Общие определения и свойства. Сходимость рядов. Признаки сходимости. (Семинар 25) Открытый урок математики во 2 классе и отчет за аттестационный период
Открытый урок математики во 2 классе и отчет за аттестационный период Урок математики в 1 классе по теме Вычитание
Урок математики в 1 классе по теме Вычитание Сложение отрицательных чисел
Сложение отрицательных чисел Степени и корни
Степени и корни Площадь фигуры
Площадь фигуры Квадратные уравнения
Квадратные уравнения Презентация отчёта плана по самообразованию на тему: Занимательные математические игры в старшем дошкольном возрасте
Презентация отчёта плана по самообразованию на тему: Занимательные математические игры в старшем дошкольном возрасте