Содержание
- 2. Учебно-исследовательская работа. Лекция 2 1 Принципы подбора выборки Результат эксперимента - некоторая совокупность измерений, которую можно
- 3. Учебно-исследовательская работа. Лекция 2 Выборка – набор значений величины {xi}, полученный из генеральной совокупности в результате
- 4. Учебно-исследовательская работа. Лекция 2 Репрезентативность выборки достигается рандомизацией или случайным отбором членов из генеральной совокупности. Это
- 5. 2 Гистограмма и полигон частот как приближение кривой распределения случайной величины Предварительная обработка данных начинается с
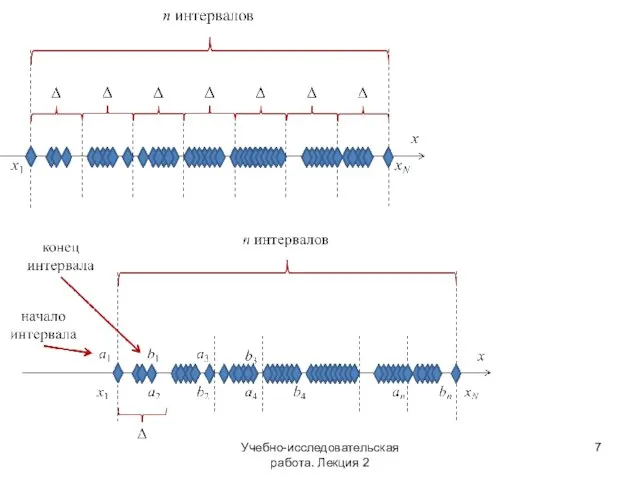
- 6. Построение вариационного ряда Группировка данных: разбиение отрезка [x1, xN] на «карманы». Как и на сколько «карманов»
- 7. Учебно-исследовательская работа. Лекция 2
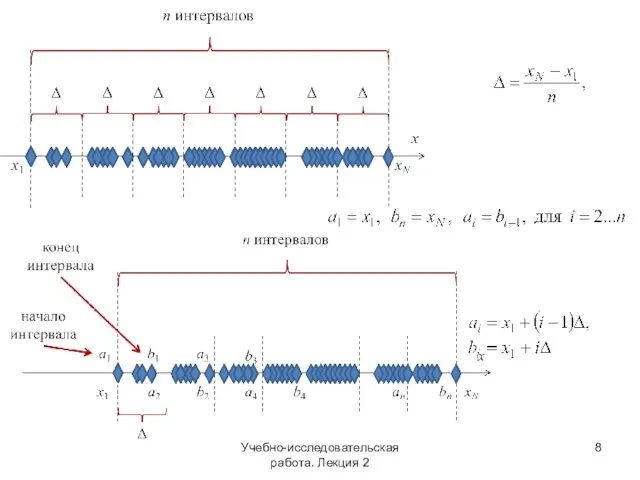
- 8. Учебно-исследовательская работа. Лекция 2
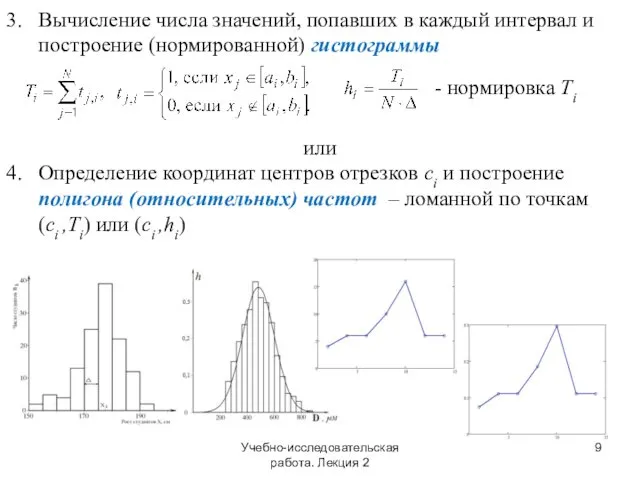
- 9. Учебно-исследовательская работа. Лекция 2 3. Вычисление числа значений, попавших в каждый интервал и построение (нормированной) гистограммы
- 10. Учебно-исследовательская работа. Лекция 2 hi ∙Δ - вероятность попадания результата отдельно измерения в данный интервал. Полная
- 11. Учебно-исследовательская работа. Лекция 2 3 Параметры распределения и их влияние на вид кривой распределения (котики) 1
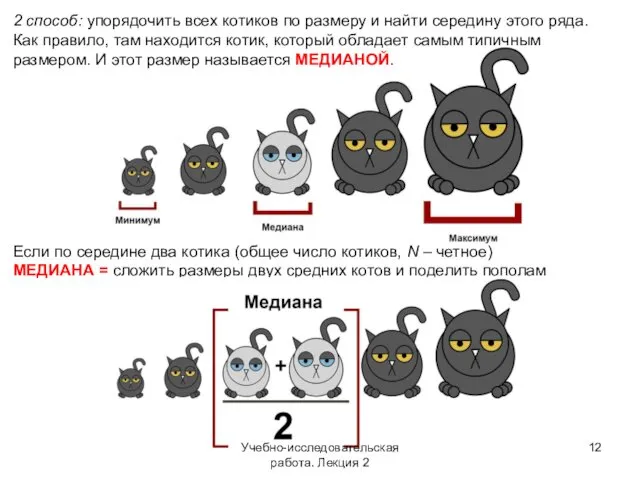
- 12. 2 способ: упорядочить всех котиков по размеру и найти середину этого ряда. Как правило, там находится
- 13. Учебно-исследовательская работа. Лекция 2 3 способ: сложить размер всех котиков, поделить на их количество – найти
- 14. Учебно-исследовательская работа. Лекция 2 НО! СРЕДНЕЕ ЗНАЧЕНИЕ чувствительно к ВЫБРОСАМ (при их наличии перестает отражать типичный
- 15. Учебно-исследовательская работа. Лекция 2 МОДА, МЕДИАНА, СРЕДНЕЕ ЗНАЧЕНИЕ - это основные методы нахождения типичного размера котиков.
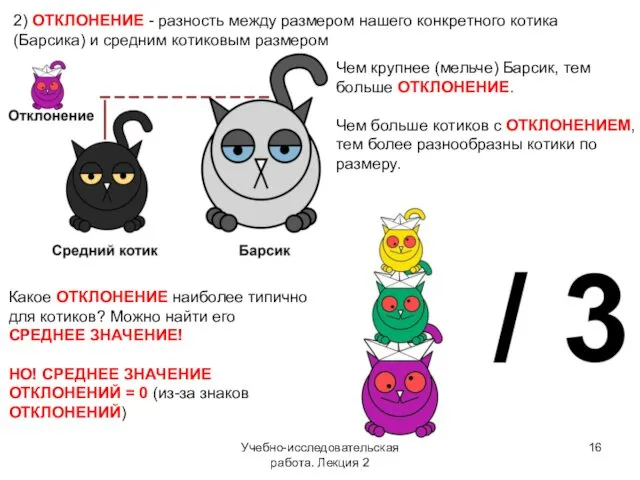
- 16. Учебно-исследовательская работа. Лекция 2 2) ОТКЛОНЕНИЕ - разность между размером нашего конкретного котика (Барсика) и средним
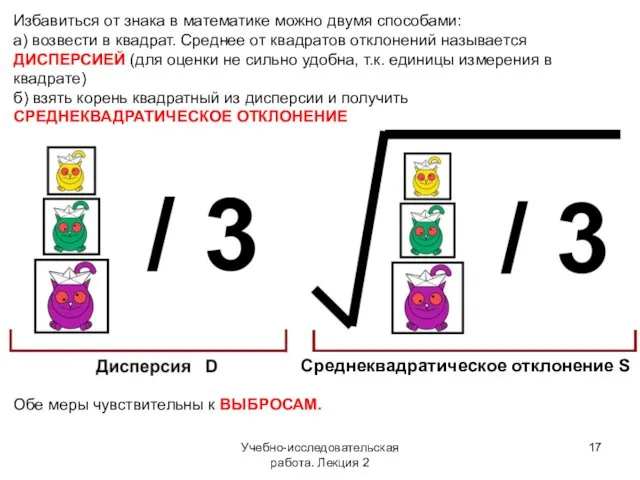
- 17. Учебно-исследовательская работа. Лекция 2 Избавиться от знака в математике можно двумя способами: а) возвести в квадрат.
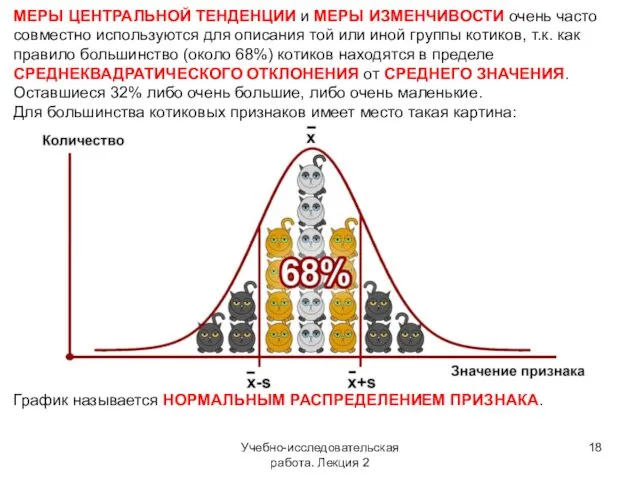
- 18. Учебно-исследовательская работа. Лекция 2 МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ и МЕРЫ ИЗМЕНЧИВОСТИ очень часто совместно используются для описания
- 19. Учебно-исследовательская работа. Лекция 2 Математически: Центр распределения характеризуется средним значением μ, медианой Me и модой Mo.
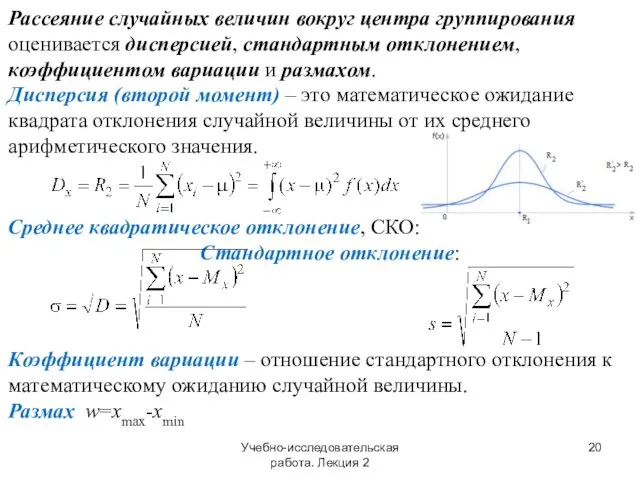
- 20. Учебно-исследовательская работа. Лекция 2 Рассеяние случайных величин вокруг центра группирования оценивается дисперсией, стандартным отклонением, коэффициентом вариации
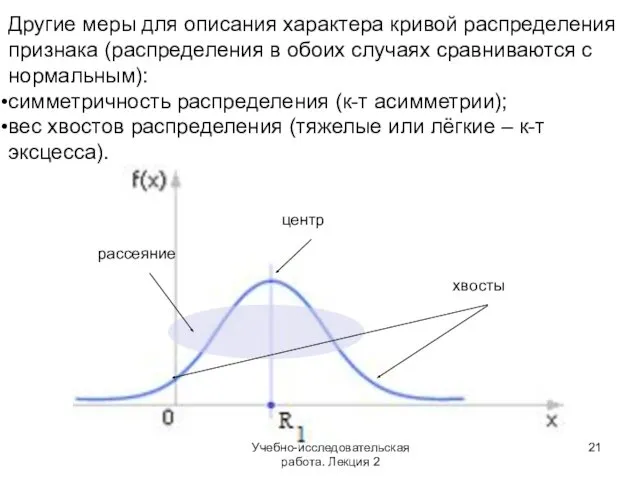
- 21. Другие меры для описания характера кривой распределения признака (распределения в обоих случаях сравниваются с нормальным): симметричность
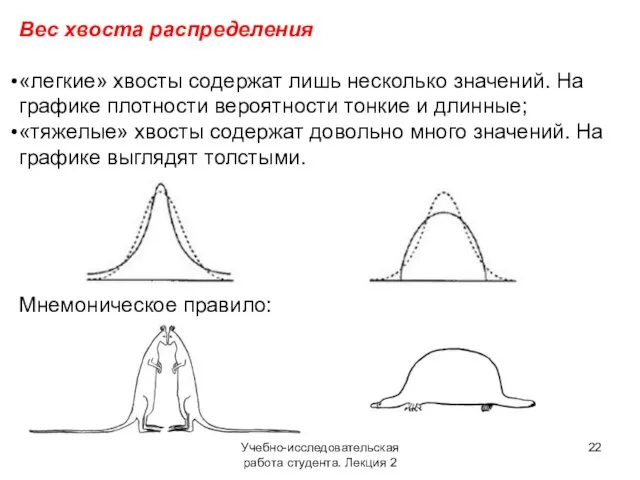
- 22. Учебно-исследовательская работа студента. Лекция 2 Вес хвоста распределения «легкие» хвосты содержат лишь несколько значений. На графике
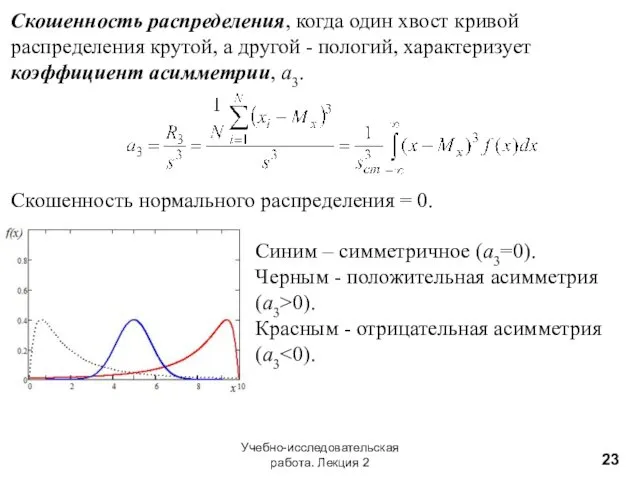
- 23. Учебно-исследовательская работа. Лекция 2 Скошенность распределения, когда один хвост кривой распределения крутой, а другой - пологий,
- 25. Скачать презентацию




![Построение вариационного ряда Группировка данных: разбиение отрезка [x1, xN] на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/105725/slide-5.jpg)






 Временные ряды и их применение для анализа и прогнозирования
Временные ряды и их применение для анализа и прогнозирования Сложение и вычитание двузначных чисел в столбик
Сложение и вычитание двузначных чисел в столбик Путешествие к Робинзону Крузо
Путешествие к Робинзону Крузо Презентация к уроку математики по теме Периметр прямоугольника
Презентация к уроку математики по теме Периметр прямоугольника Практическое применение интегралов в различных областях
Практическое применение интегралов в различных областях Умножение и деление десятичных дробей на 10,100
Умножение и деление десятичных дробей на 10,100 Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия Ряд Фурье. Преобразование Фурье, его свойства. Дискретное преобразование Фурье. Быстрое преобразование Фурье. Лекция 8
Ряд Фурье. Преобразование Фурье, его свойства. Дискретное преобразование Фурье. Быстрое преобразование Фурье. Лекция 8 Нахождение неизвестного третьего слагаемого. Задачи
Нахождение неизвестного третьего слагаемого. Задачи Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Длина окружности
Длина окружности Сравнение десятичных дробей. Урок математики в 5 классе
Сравнение десятичных дробей. Урок математики в 5 классе Сравнение отрезков и углов
Сравнение отрезков и углов Понятие непрерывной случайной величины. 10 класс
Понятие непрерывной случайной величины. 10 класс Способы доказательства теоремы Пифагора
Способы доказательства теоремы Пифагора презентация к уроку по математике во 2 классе. Тема: Уравнение. Решение уравнений методом подбора
презентация к уроку по математике во 2 классе. Тема: Уравнение. Решение уравнений методом подбора Сложение и вычитание одночленов
Сложение и вычитание одночленов Построение правильных многоугольников
Построение правильных многоугольников Параллельные прямые
Параллельные прямые Поворот
Поворот Приёмы умножения числа 2. Деление на 2
Приёмы умножения числа 2. Деление на 2 Решение задач с помощью дробно-рациональных уравнений
Решение задач с помощью дробно-рациональных уравнений Признак перпендикулярности прямой и плоскости. (10 класс)
Признак перпендикулярности прямой и плоскости. (10 класс) Дисперсия числового набора. 8 класс
Дисперсия числового набора. 8 класс Определенный интеграл. Формула интегрирования по частям (пример 2)
Определенный интеграл. Формула интегрирования по частям (пример 2) Понятие первообразной. 11 класс
Понятие первообразной. 11 класс Тригонометричні формули додавання та наслідки з них
Тригонометричні формули додавання та наслідки з них Модульное планирование курса математики. 5 класс
Модульное планирование курса математики. 5 класс