Понятие первообразной. 11 класс презентация

СОДЕРЖАНИЕ
понятие первообразной
неопределенный интеграл
таблица первообразных
три правила нахождения первообразных
определенный интеграл
вычисление определенного интеграла
площадь криволинейной трапеции
площадь криволинейной трапеции площадь криволинейной трапеции (1)
площадь криволинейной трапеции площадь криволинейной трапеции (2)
площадь криволинейной трапеции площадь криволинейной трапеции (3)
площадь криволинейной трапеции площадь криволинейной трапеции ( площадь криволинейной трапеции (4 площадь криволинейной трапеции (4)
пример (1)
пример (2)

Как по скорости движения тела найти закон его движения?

ПОНЯТИЕ ПЕРВООБРАЗНОЙ
Функцию F(x) называют первообразной для функции f(x) на интервале (a; b), если на нем производная функции F(x) равна f(x):
Операцию, обратную дифференцированию называют интегрированием.

Примеры
f(x) = 2x; F(x) = x2
F′(x)= (x2)′ = 2x = f(x)
f(x) = – sin x; F(x) = сos x
F′(x)= (cos x)′ = – sin x = f(x)
f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F′(x)= (2x3 + 4x)′ = 6x2 + 4 = f(x)
f(x) = 1/cos2 x; F(x) = tg x
F′(x)= (tg x)′ = 1/cos2 x= f(x)

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x) называют любую ее первообразную функцию.
Где С – произвольная постоянная (const).

Примеры

Три правила нахождения первообразных
1º Если F(x) есть первообразная для f(x), а G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf(х).

ТАБЛИЦА ПЕРВООБРАЗНЫХ
f(x)
F(x)
F(x)

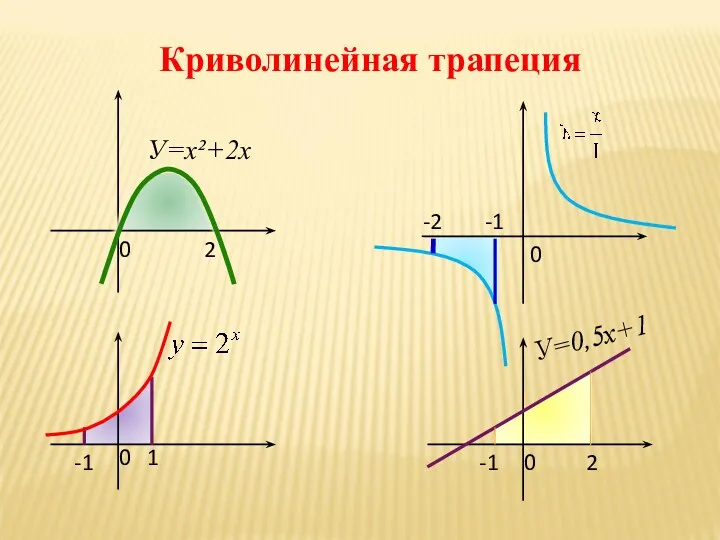
Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной трапеции
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].

Криволинейная трапеция
0
2
0
0
0
1
-1
-1
2
-1
-2
У=х²+2х
У=0,5х+1

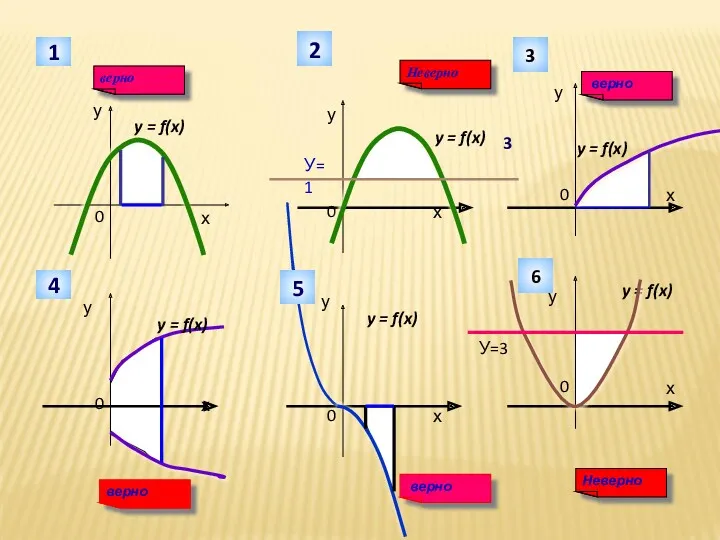
у
1
Неверно
у
у
у
у
у
У=1
2
верно
3
3
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
У=3
4
5
6
верно
Неверно верно
верно

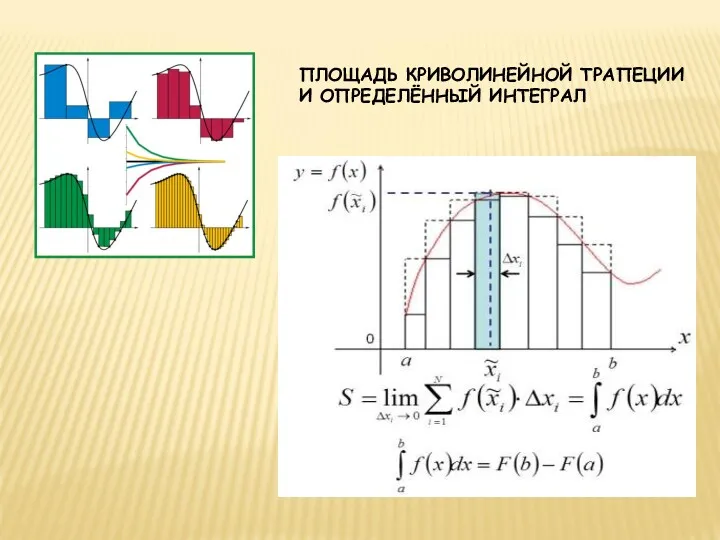
ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
И ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

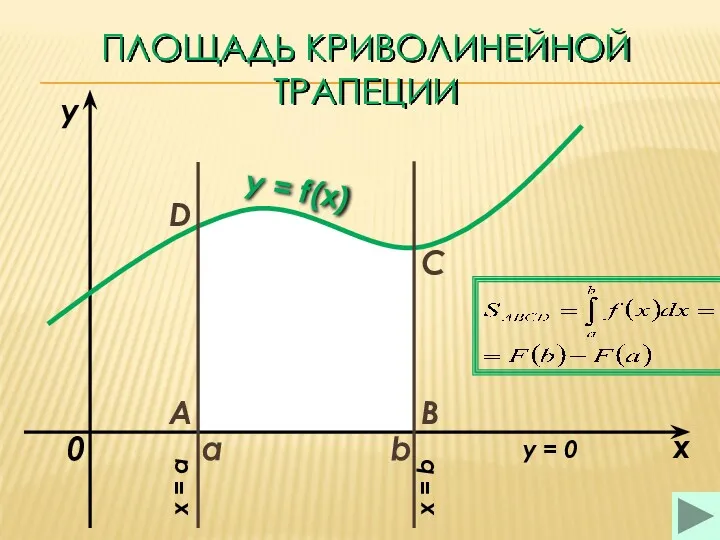
Площадь криволинейной трапеции.
где F(x) – любая первообразная функции f(x).

Формула Ньютона-Лейбница
1643—1727
1646—1716

ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y = 0

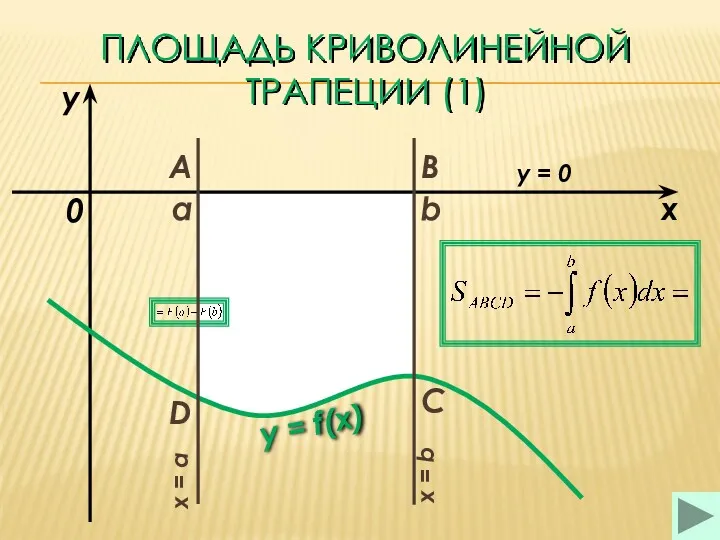
ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ (1)
a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y = 0

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D
M
P
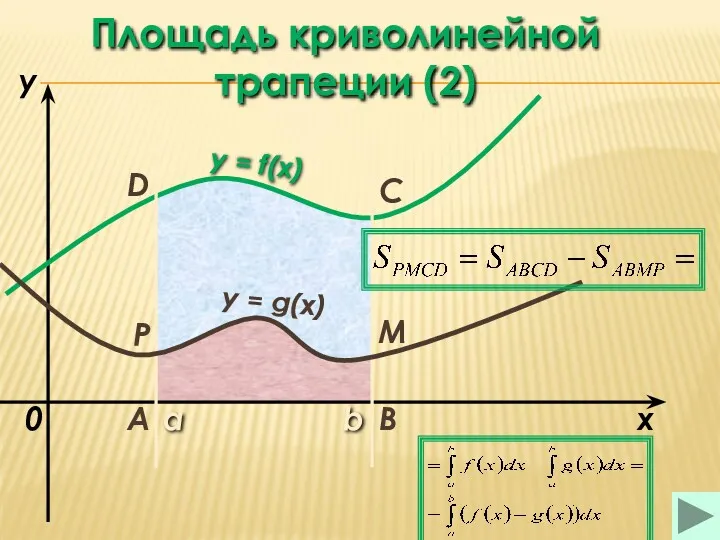
Площадь криволинейной трапеции (2)

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (3)

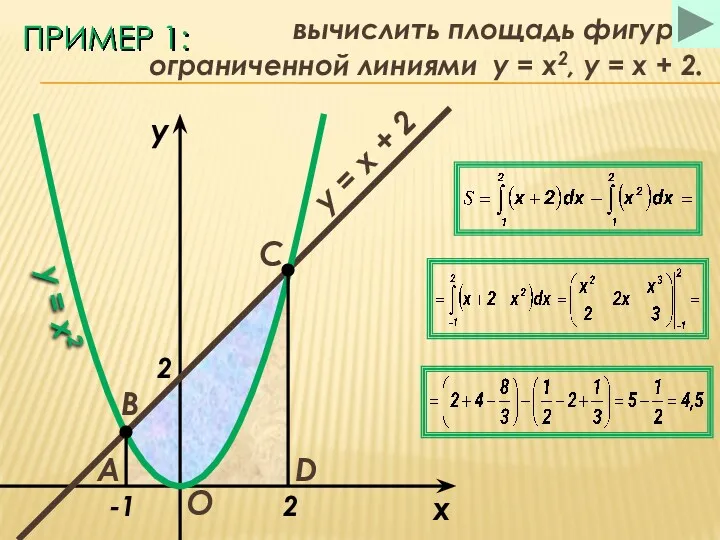
ПРИМЕР 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
x
y
y = x2
y = x + 2
-1
2
A
B
O
D
C
2

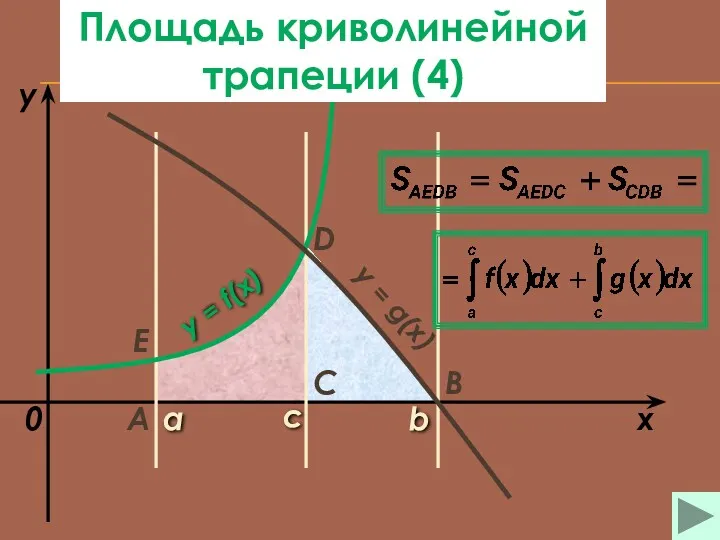
a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D
с
Е
Площадь криволинейной трапеции (4)

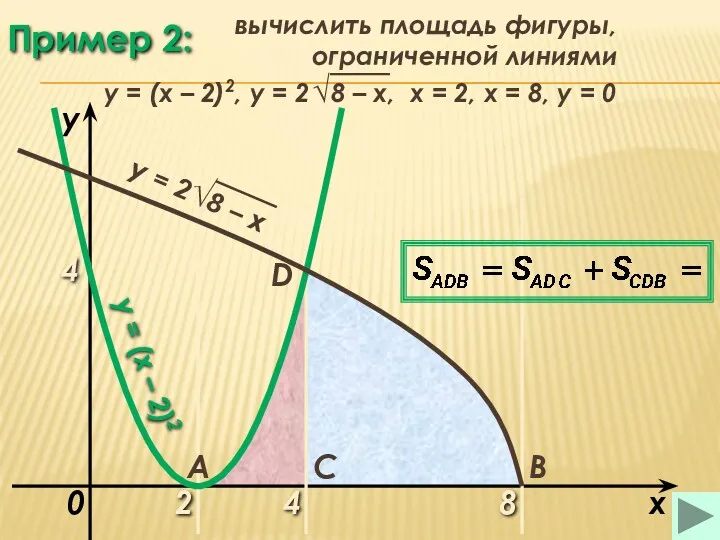
Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y
4

Пример 2:

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.