Содержание
- 2. ПОСТАНОВКА ЗАДАЧИ Дано F(x)=0, где F(x) определена на [a;b] и удовлетворяет следующим условиям: F(x) непрерывна и
- 3. СУТЬ МЕТОДА ХОРД 1. Нелинейная функция f(x) на отделенном отрезке заменяется прямой линией – хордой, стягивающей
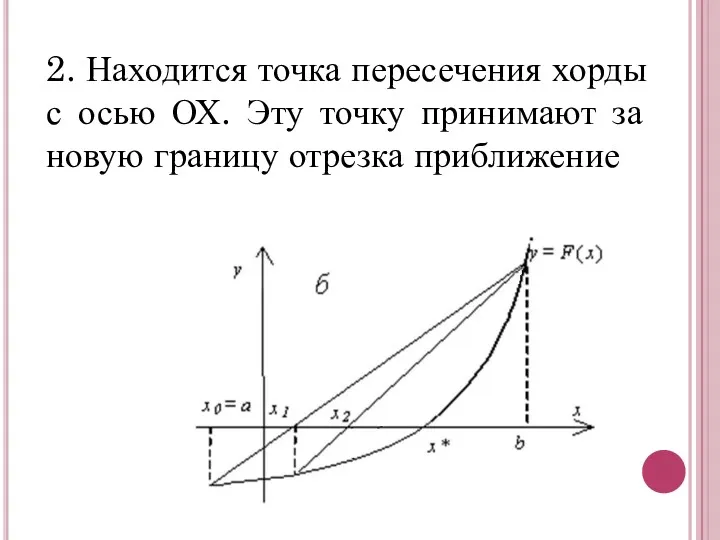
- 4. 2. Находится точка пересечения хорды с осью ОХ. Эту точку принимают за новую границу отрезка приближение
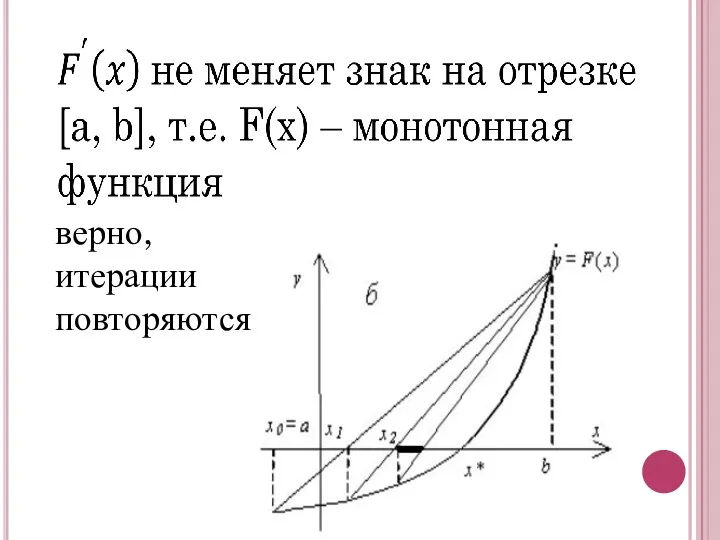
- 5. верно, итерации повторяются
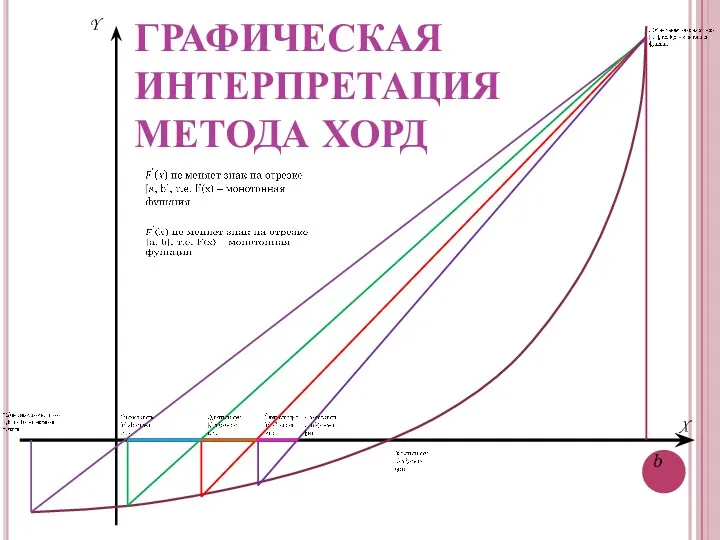
- 6. X Y b ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА ХОРД
- 7. ВАРИАНТЫ АЛГОРИТМА МЕТОДА f(b) f"(b)>0
- 9. РЕШИТЬ УРАВНЕНИЕ
- 10. f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2 f(0) = 1,5 > 0.
- 11. Для вычислений применяем следующую формулу
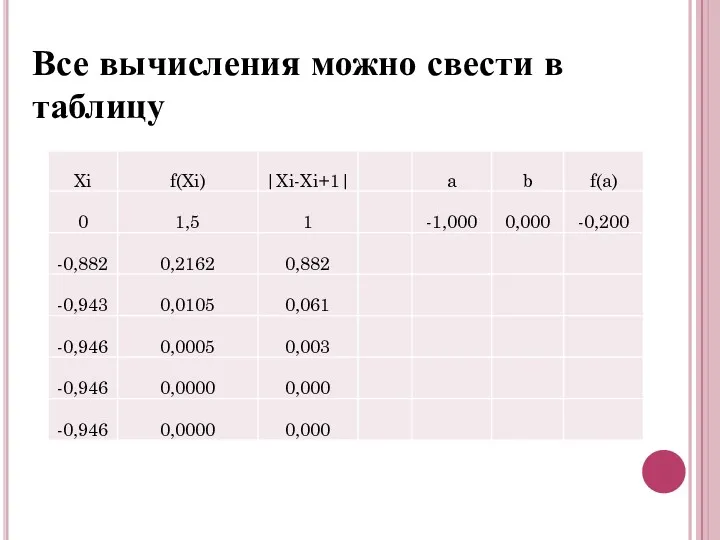
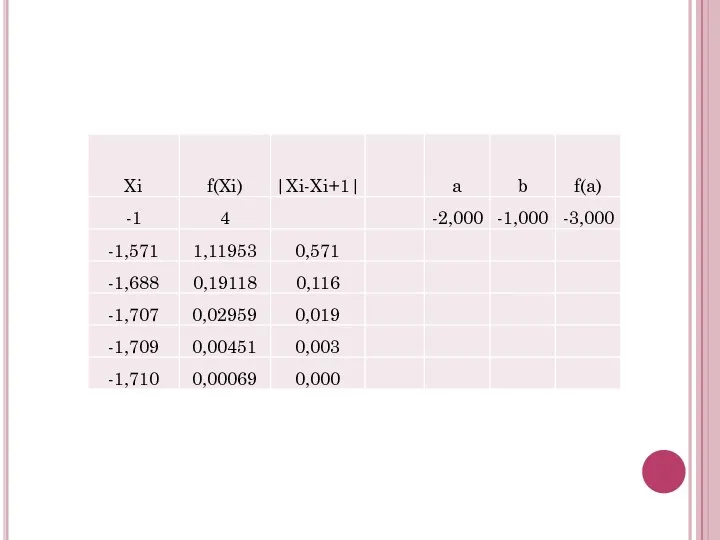
- 12. Все вычисления можно свести в таблицу
- 13. РЕШИТЬ УРАВНЕНИЕ
- 14. f"(х) = 6х f(-2) = -3 f(-1) = 4 > 0. f"(-2) = -12 f"(-1) =
- 15. Для вычислений применяем следующую формулу
- 17. Домашнее задание: решить уравнение методом хорд x3‑ 6x2+3x+11=0
- 18. ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Метод Ньютона (касательных)
- 19. ИДЕЯ МЕТОДА аналогична той, которая реализована в методе хорд, только в качестве прямой берется касательная, проводимая
- 20. Выбор начальной точки зависит от свойств функции:
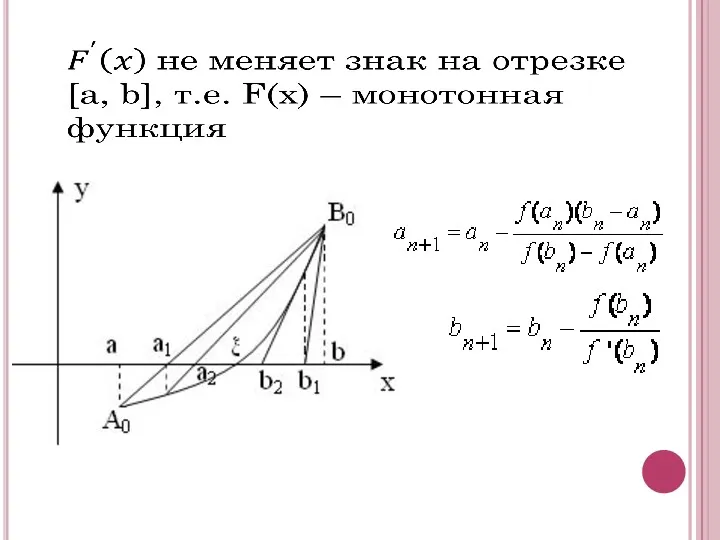
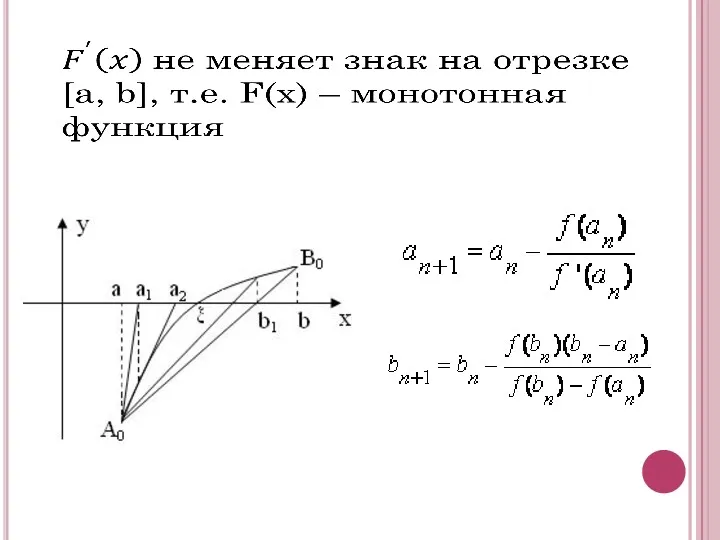
- 21. Очередное приближение вычисляется по формуле: Вычисления продолжаются до тех пор, пока
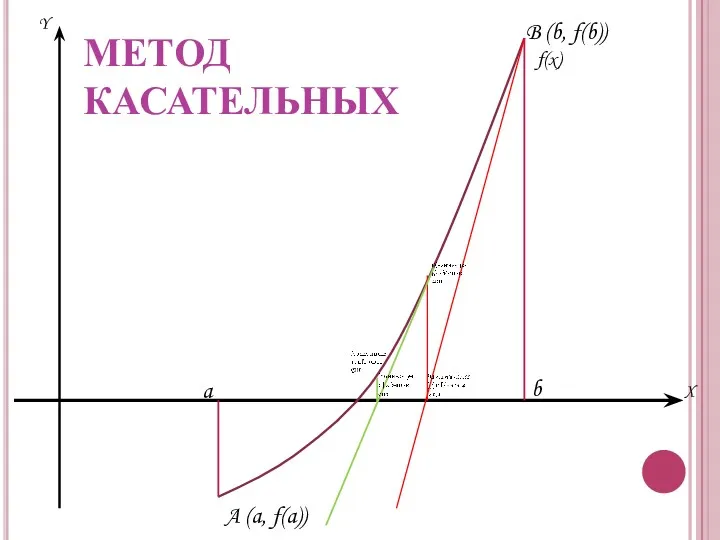
- 22. Y X B (b, f(b)) A (a, f(a)) f(x) b a МЕТОД КАСАТЕЛЬНЫХ
- 23. ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Комбинирован-ный метод
- 27. Пример Дано уравнение: x3 – 2х2 – 4х + 7 = 0. Найти корень на отрезке
- 28. Вывод: условие выполняется для левой стороны отрезка, т.е. с правой стороны будем приближаться методом хорд, а
- 30. Скачать презентацию
![ПОСТАНОВКА ЗАДАЧИ Дано F(x)=0, где F(x) определена на [a;b] и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/184827/slide-1.jpg)



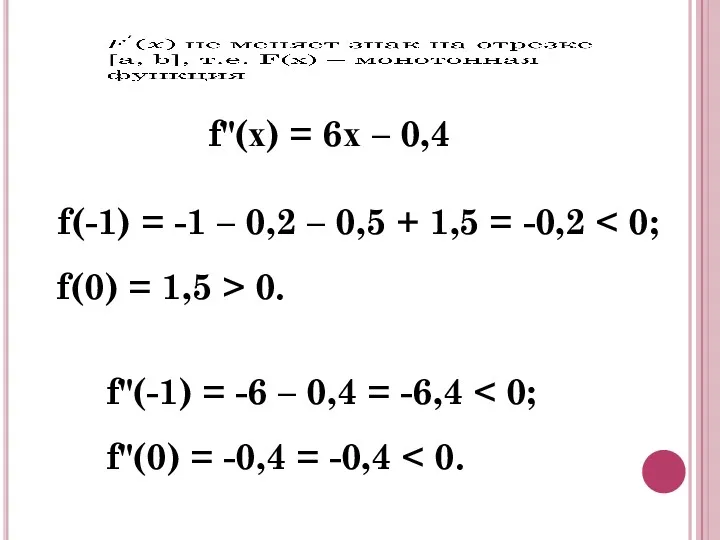


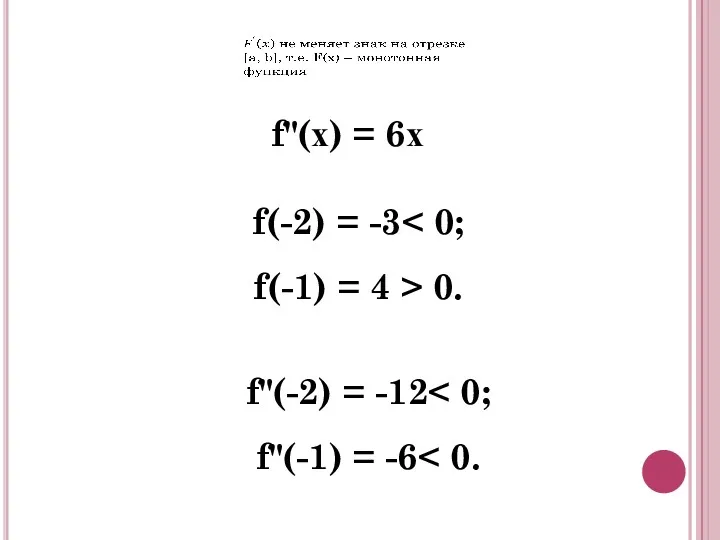










 Дроби в стране Мульти Пульти
Дроби в стране Мульти Пульти Параллельный перенос графика функции
Параллельный перенос графика функции Лас су желісі
Лас су желісі Число и цифра 8.
Число и цифра 8. Клуб влюблённых в математику, 4 класс.1, 2 занятие.
Клуб влюблённых в математику, 4 класс.1, 2 занятие. Пропорция
Пропорция Успоредни линии. Триъгълници
Успоредни линии. Триъгълници Площадь прямоугольника. единицы площади.
Площадь прямоугольника. единицы площади. Решение логарифмических уравнений
Решение логарифмических уравнений Определенный интеграл и его свойства. Формула Ньютона-Лейбница
Определенный интеграл и его свойства. Формула Ньютона-Лейбница Все действия с натуральными числами
Все действия с натуральными числами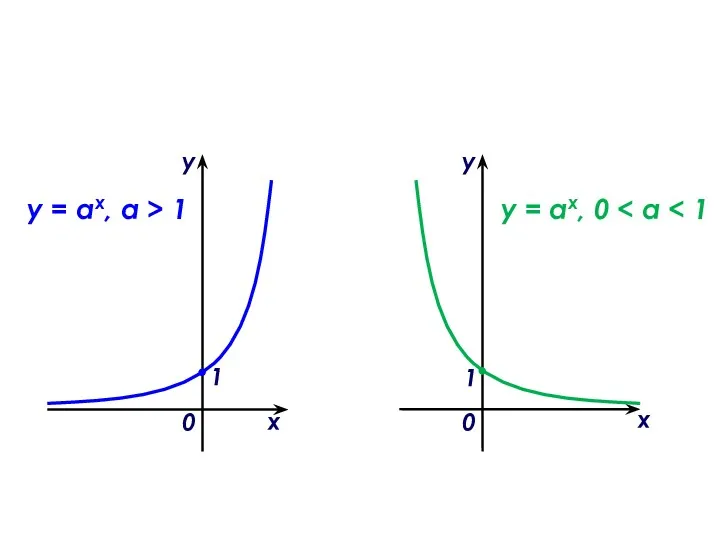 Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Целые уравнения
Целые уравнения Нумерация многозначных чисел. Сложение и вычитание многозначных чисел. Решение уравнений и задач
Нумерация многозначных чисел. Сложение и вычитание многозначных чисел. Решение уравнений и задач Учебно-исследовательский проект Математика в профессиях
Учебно-исследовательский проект Математика в профессиях урок математики 4 класс Технологическая карта урока.
урок математики 4 класс Технологическая карта урока.  Элементы теории вероятностей. Элементы математической статистики
Элементы теории вероятностей. Элементы математической статистики Логарифмы вокруг нас
Логарифмы вокруг нас Задачи на движение по реке
Задачи на движение по реке Первообразная функции. Неопределенный интеграл
Первообразная функции. Неопределенный интеграл Решение задач на деление дробей
Решение задач на деление дробей Задачи, 1 класс
Задачи, 1 класс Mathematics and visual arts
Mathematics and visual arts Логическая математика. Занятие математического кружка в 4 классе
Логическая математика. Занятие математического кружка в 4 классе Решение задач. Прямоугольный треугольник
Решение задач. Прямоугольный треугольник Устный счет к уроку математики
Устный счет к уроку математики Работа над задачей по системе Л.В.Занкова
Работа над задачей по системе Л.В.Занкова Теорема об отрезках пересекающихся хорд
Теорема об отрезках пересекающихся хорд