Содержание
- 2. Решение задач интерполяции в теплоэнергетике В результате эксперимента по определению холостого хода определена зависимость потребляемой из
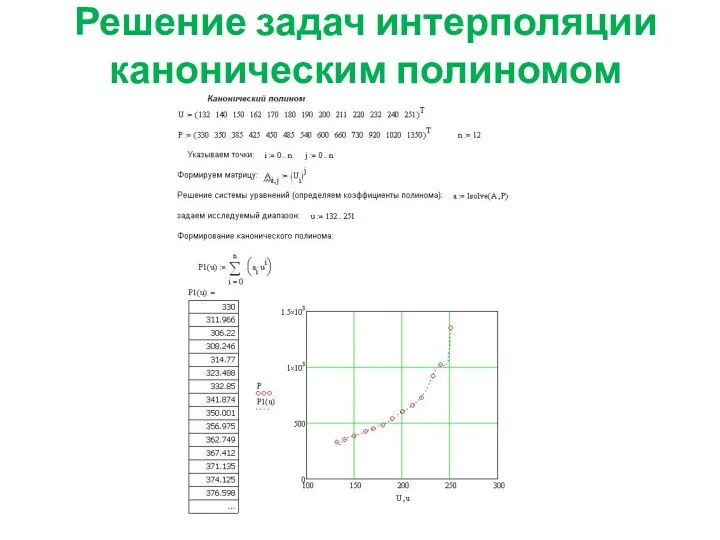
- 3. Решение задач интерполяции каноническим полиномом
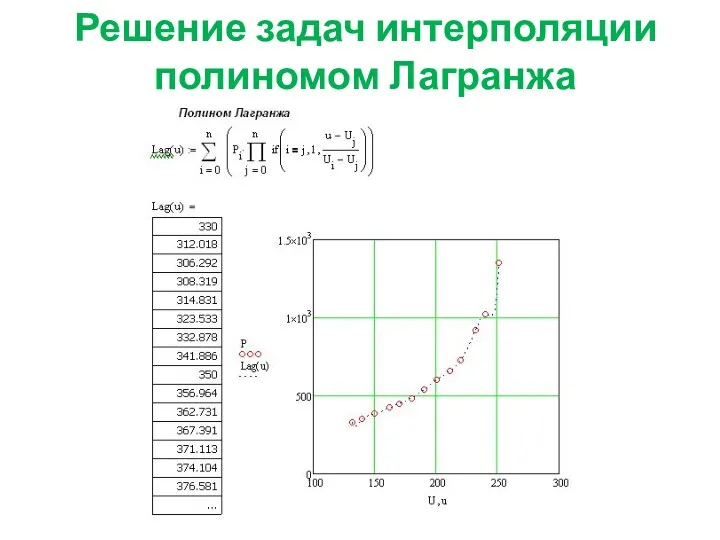
- 4. Решение задач интерполяции полиномом Лагранжа
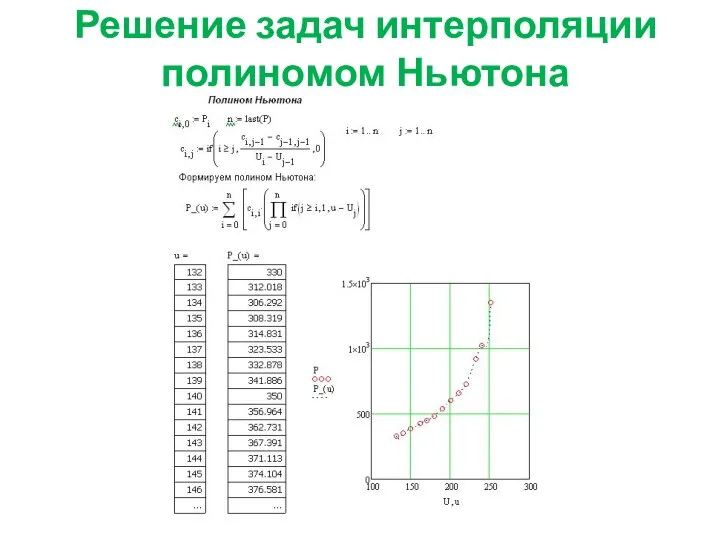
- 5. Решение задач интерполяции полиномом Ньютона
- 6. Сравнение решения задачи интерполяции разными методами
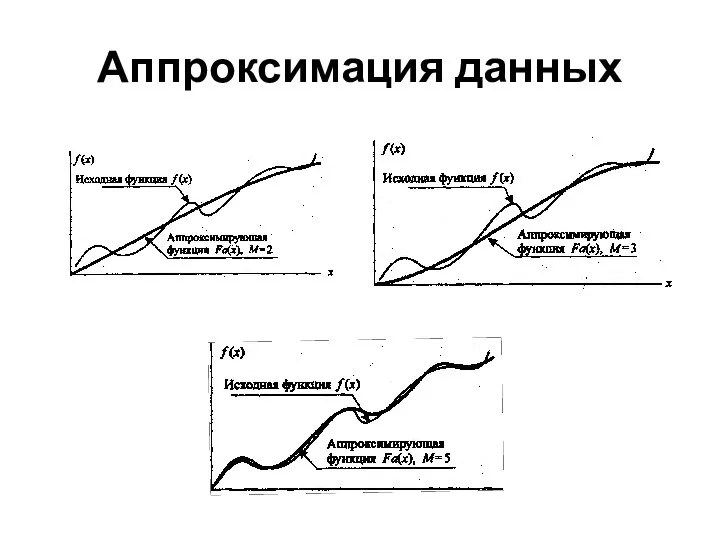
- 7. Аппроксимация данных Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около
- 8. Аппроксимация данных Близость исходной и аппроксимирующей функций определяется числовой мерой – критерием аппроксимации (близости). Наибольшее распространение
- 9. Аппроксимация данных Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием
- 10. Аппроксимация данных
- 11. Метод наименьших квадратов Метод базируется на применении в качестве критерия близости суммы квадратов отклонений заданных и
- 12. Метод наименьших квадратов Искомые переменные aj можно найти из необходимого условия минимума R по этим переменным,
- 13. Метод наименьших квадратов После очевидных преобразований (сокращение на два, раскрытие скобок, изменение порядка суммирования) получим: где
- 14. Метод наименьших квадратов Получилась система n+1 уравнений с таким же количеством неизвестных aj, причем линейная относительно
- 15. Метод наименьших квадратов - полином 1 порядка - полином n-го порядка
- 16. Метод наименьших квадратов Дана таблично заданная функция (табл. 1.1.). Требуется найти аппроксимирующую функцию в виде линейного
- 17. Метод наименьших квадратов Проведя преобразования, получим:
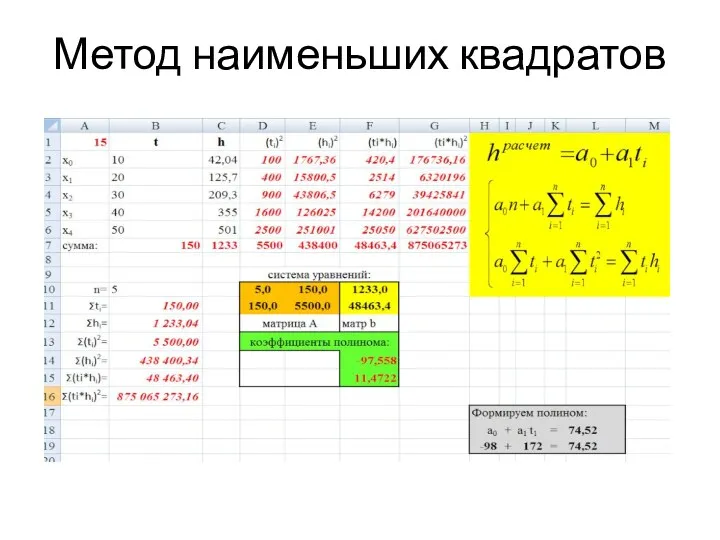
- 18. Метод наименьших квадратов Система нормальных уравнений для полинома 1 степени будет выглядеть следующим образом: Используя имеющиеся
- 19. Метод наименьших квадратов
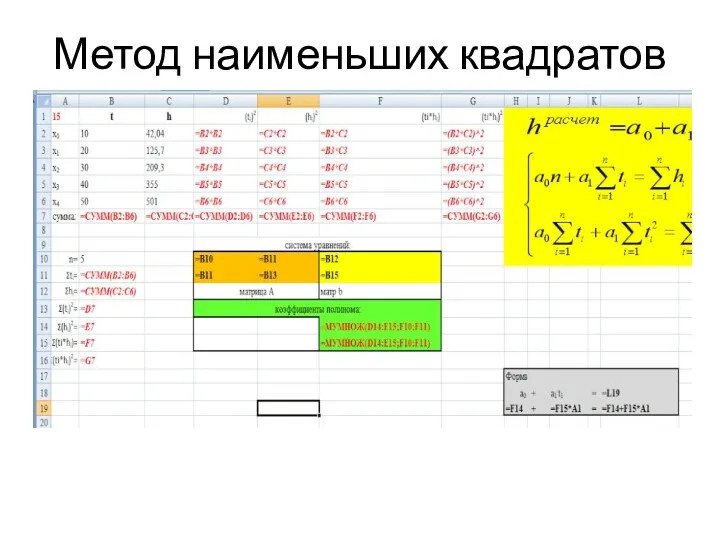
- 20. Метод наименьших квадратов
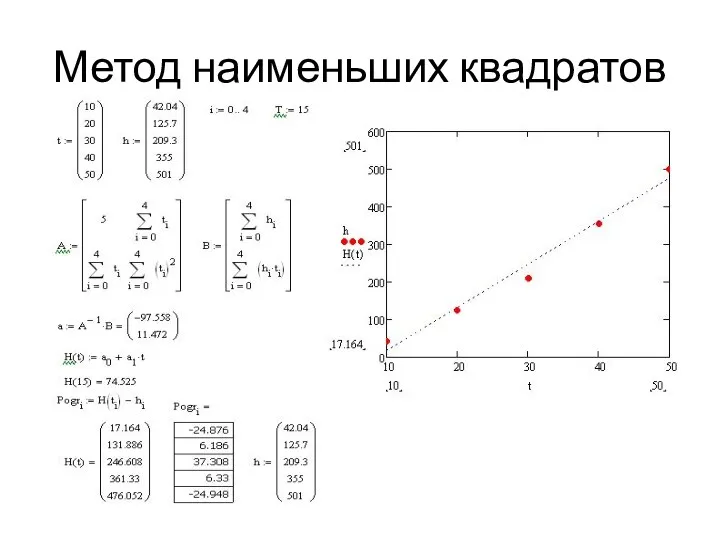
- 21. Метод наименьших квадратов
- 22. Метод неопределенных коэффициентов Метод базируется на составлении и решении системы линейных уравнений. При заданной системе уравнений
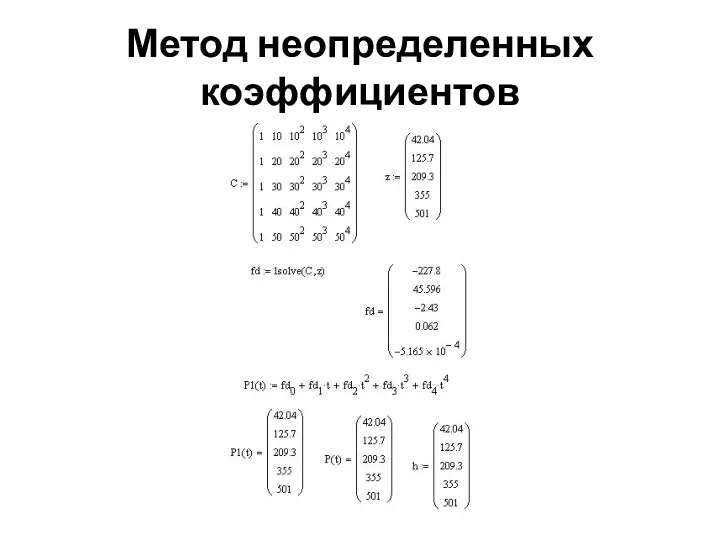
- 23. Метод неопределенных коэффициентов Затем строим матрицу: Решаем систему (находим коэффициенты полинома) и формируем полином n-ой степени.
- 24. Метод неопределенных коэффициентов
- 26. Скачать презентацию















 Урок математики в 1 классе по теме: Задача
Урок математики в 1 классе по теме: Задача Визначений інтеграл
Визначений інтеграл Линейные преобразования: основные понятия и определения
Линейные преобразования: основные понятия и определения презентация для 3 класса
презентация для 3 класса Различные методы решения неравенств. Общие методы решения неравенств
Различные методы решения неравенств. Общие методы решения неравенств Меры объёма. Литр
Меры объёма. Литр Сложение и вычитание десятичных дробей 5 класс
Сложение и вычитание десятичных дробей 5 класс Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Дополнительная Программа
Дополнительная Программа Презентация к уроку математики по теме Умножение и деление чисел, оканчивающихся нулями
Презентация к уроку математики по теме Умножение и деление чисел, оканчивающихся нулями Презентация к уроку. Математика 4 класс. Тема Итоговое повторение
Презентация к уроку. Математика 4 класс. Тема Итоговое повторение Сравнение дробей с разными знаменателями. 6 класс
Сравнение дробей с разными знаменателями. 6 класс Графики. 6 класс
Графики. 6 класс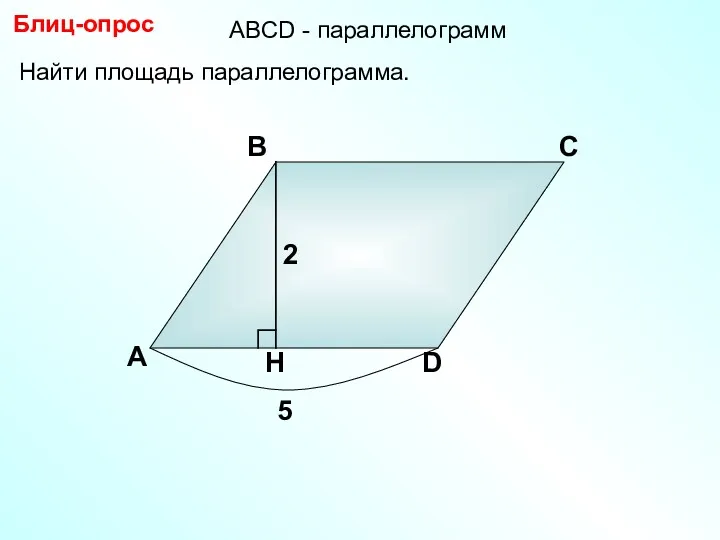 Площадь параллелограмма. Блиц-опрос
Площадь параллелограмма. Блиц-опрос Презентация к уроку математики в 4 классе Составление уравнений по условию, по схеме Программа Гармония
Презентация к уроку математики в 4 классе Составление уравнений по условию, по схеме Программа Гармония Решение задач с процентами: нахождение числа по процентам. 5 класс
Решение задач с процентами: нахождение числа по процентам. 5 класс Алгоритм сложения чисел с переходом через десяток
Алгоритм сложения чисел с переходом через десяток Векторы. Векторные и скалярные величины
Векторы. Векторные и скалярные величины Решение задач с помощью уравнений
Решение задач с помощью уравнений Урок математики в 4 классе (Л.Занков) по теме Округление чисел
Урок математики в 4 классе (Л.Занков) по теме Округление чисел Теорема Пика
Теорема Пика Составление таблиц истинности для сложных высказываний
Составление таблиц истинности для сложных высказываний Алгебра высказываний
Алгебра высказываний Шкалы и координаты
Шкалы и координаты Метод растянутых координат. (Лекция 9)
Метод растянутых координат. (Лекция 9) Симметрия на координатной плоскости. 6 класс
Симметрия на координатной плоскости. 6 класс Перпендикуляр и наклонная. Расстояние от точки до плоскости
Перпендикуляр и наклонная. Расстояние от точки до плоскости Арифметический корень натуральной степени
Арифметический корень натуральной степени