Содержание
- 2. Лекция 5 2. Методы интегрирования. 3. Классы интегрируемых функций. 1. Неопределенный интеграл и его свойства. Интегральное
- 3. Неопределенный интеграл и его свойства. Примеры. 1. 2. 3.
- 4. Если F1(x) и F2(x) - две первообразные для f(x) на (a,b), то F1(x) = F2(x) +
- 5. Доказательство. Вывод. Если F(x) - первообразная для функции f(x) на интервале (a,b), то Ф(х) = F(x)+
- 6. Обозначение неопределённого интеграла:
- 7. Свойства неопределенного интеграла. 1. 2. 3. 4.
- 8. Таблица неопределенных интегралов.
- 11. I. Замена переменной в неопределенном интеграле.
- 12. Доказательство. Производная левой части: Производная правой части:
- 13. Замечание. Формулой замены переменной можно пользоваться “слева - направо’’ и “справа - налево’’ (подведение новой переменной
- 14. II. Интегрирование по частям. Рассмотрим
- 15. Примеры.
- 16. Замечание. Формулу интегрирования по частям можно применять несколько раз. за u обозначается логарифм или обратная тригонометрическая
- 18. Такие интегралы называются возвратными.
- 19. Классы интегрируемых функций. Простейшие дроби. К простейшим дробям относятся: A,M,N,a,p,q - действительные числа, n – натуральное
- 21. Здесь
- 27. - рекуррентная (возвратная) формула.
- 29. Скачать презентацию


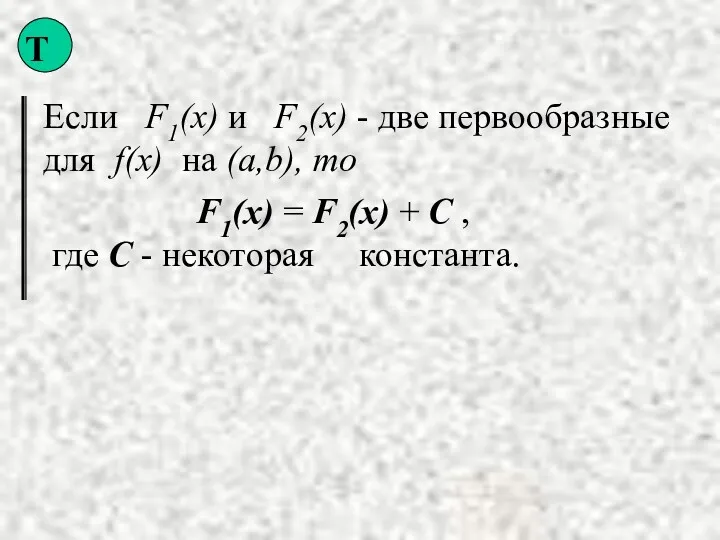




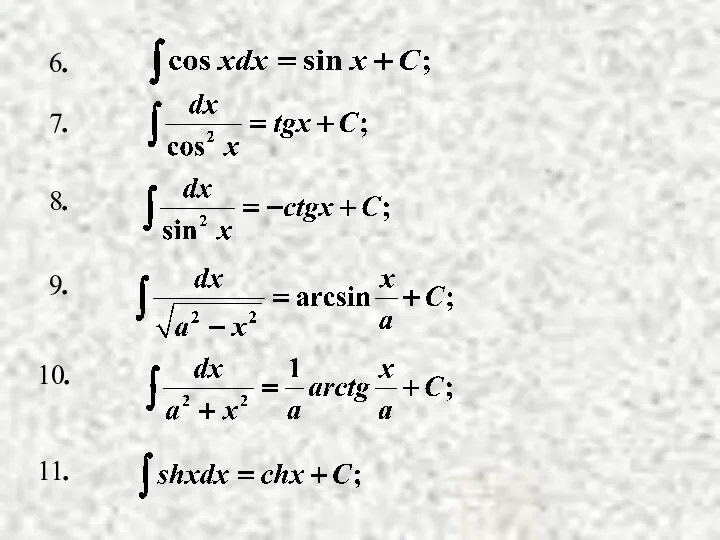
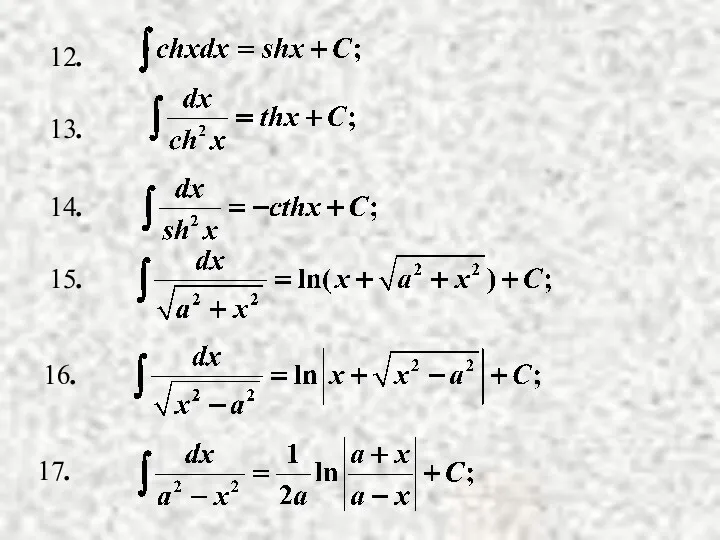

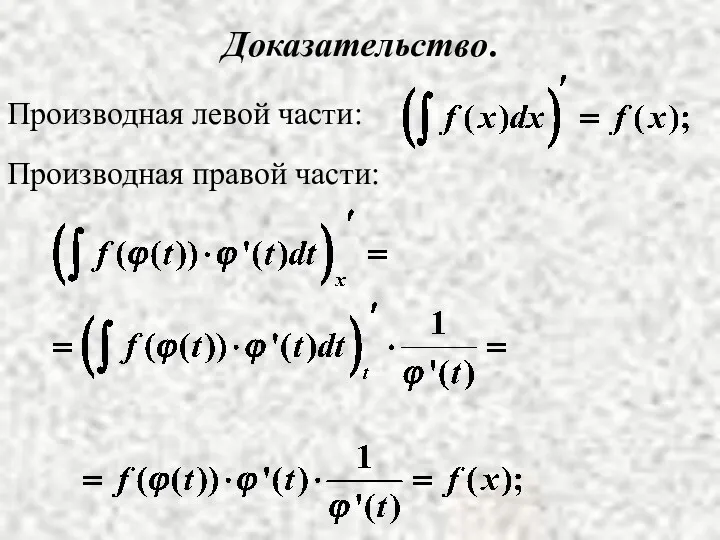


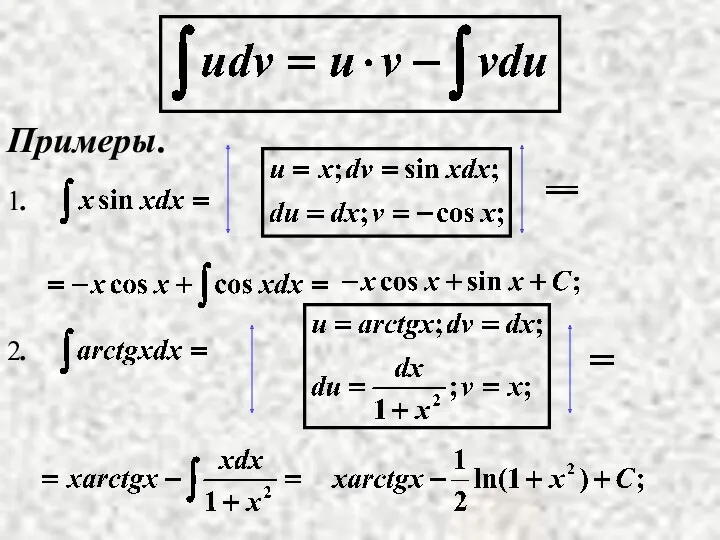





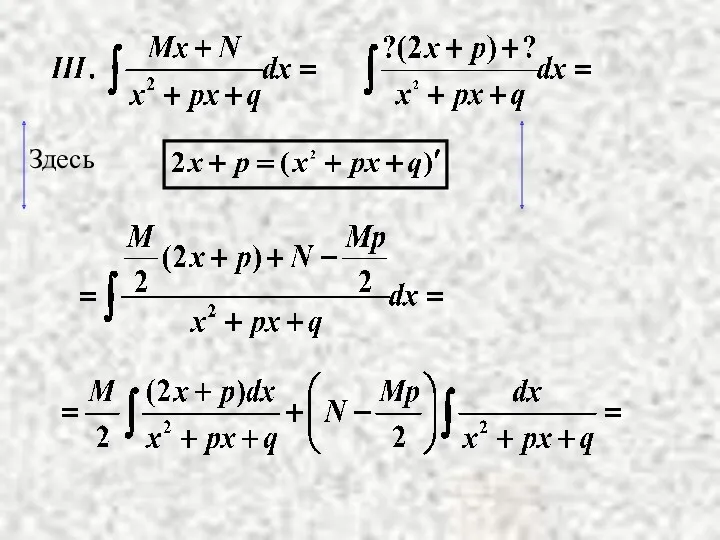
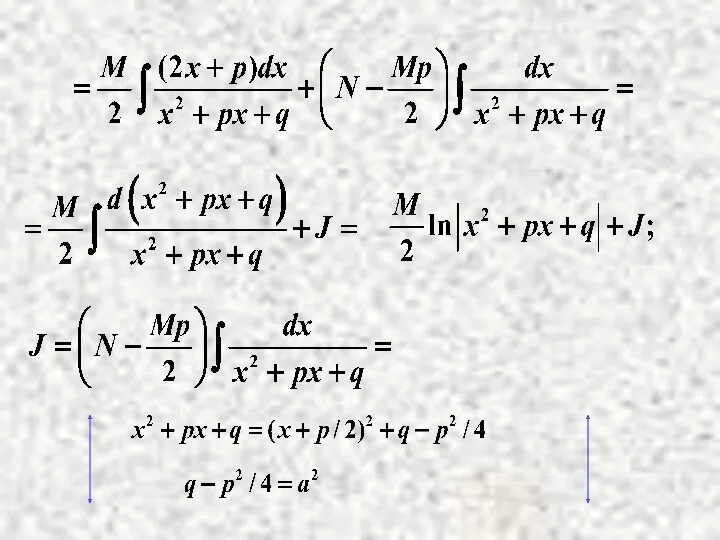

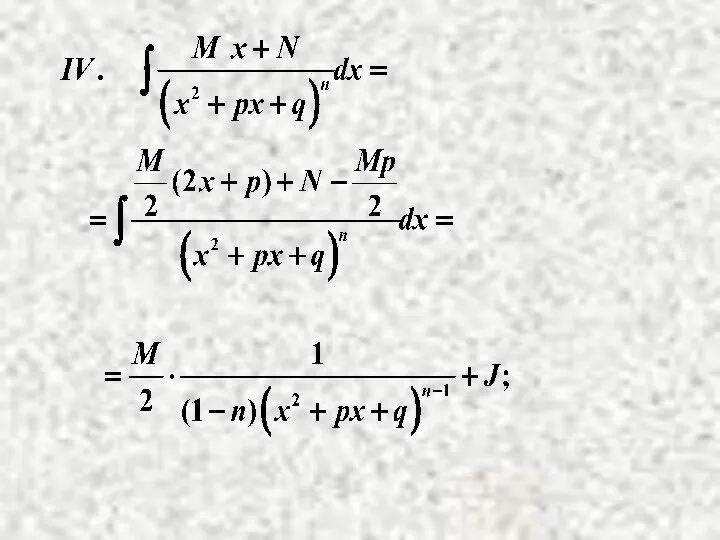



 Урок математики в 1 классе по теме Знакомство с понятием Уравнение
Урок математики в 1 классе по теме Знакомство с понятием Уравнение Единицы измерения в разных странах
Единицы измерения в разных странах ГИА. Открытый банк заданий по математике. Задача
ГИА. Открытый банк заданий по математике. Задача Треугольник вписанный в окружность
Треугольник вписанный в окружность Свойства параллельных прямых
Свойства параллельных прямых Элементы теории вероятностей и математической статистики
Элементы теории вероятностей и математической статистики Симметрия вокруг нас
Симметрия вокруг нас ЕГЭ по математике. Вариант 1
ЕГЭ по математике. Вариант 1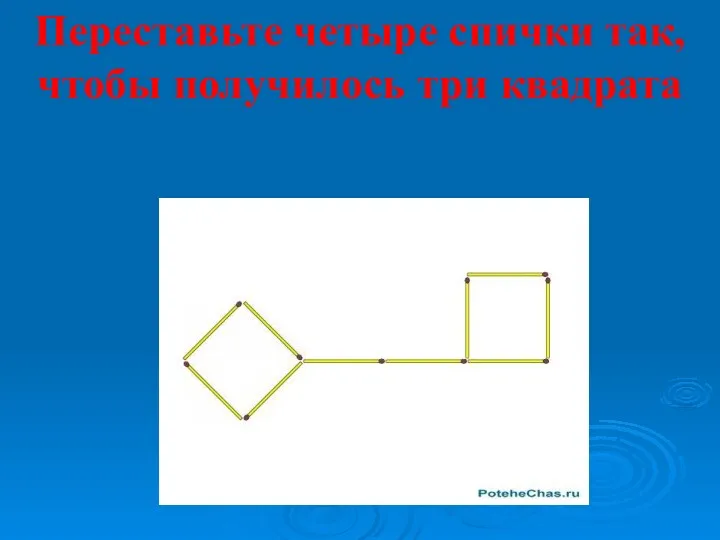 Игры со спичками
Игры со спичками Тетраэдр. Задания для устного счета. Упражнение 5
Тетраэдр. Задания для устного счета. Упражнение 5 Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Противоположные числа и модуль числа
Противоположные числа и модуль числа Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Площадь трапеции
Площадь трапеции Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций
Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Параллельные прямые
Параллельные прямые Презентация к мастер-классу Системно-деятельностный подход при решении задач
Презентация к мастер-классу Системно-деятельностный подход при решении задач Свойства прямоугольных треугольников. 7 класс
Свойства прямоугольных треугольников. 7 класс Виды симметрии. Центральная и осевая симметрия
Виды симметрии. Центральная и осевая симметрия Решение задач с применением диаграмм Эйлера-Венна
Решение задач с применением диаграмм Эйлера-Венна Тригонометрические уравнения. Отбор корней с помощью графиков
Тригонометрические уравнения. Отбор корней с помощью графиков Музыкальные инструменты для детей
Музыкальные инструменты для детей Практикум по решению ключевых типов задач по теории вероятностей. Часть 2. 11 класс
Практикум по решению ключевых типов задач по теории вероятностей. Часть 2. 11 класс Математическое моделирование автоматических систем регулирования
Математическое моделирование автоматических систем регулирования Регрессио́нный анализ. Примеры применения регрессионного анализа
Регрессио́нный анализ. Примеры применения регрессионного анализа Случаи сложения и вычитания, основанные на знании нумерации чисел
Случаи сложения и вычитания, основанные на знании нумерации чисел Решение систем уравнений способом сложения
Решение систем уравнений способом сложения