Содержание
- 2. 1.Возрастание и убывание функции. 2. Максимум и минимум функции. 3.Наибольшее и наименьшее значения функции на отрезке.
- 3. Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то функция возрастает на этом промежутке. Теорема
- 4. Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке. Теорема
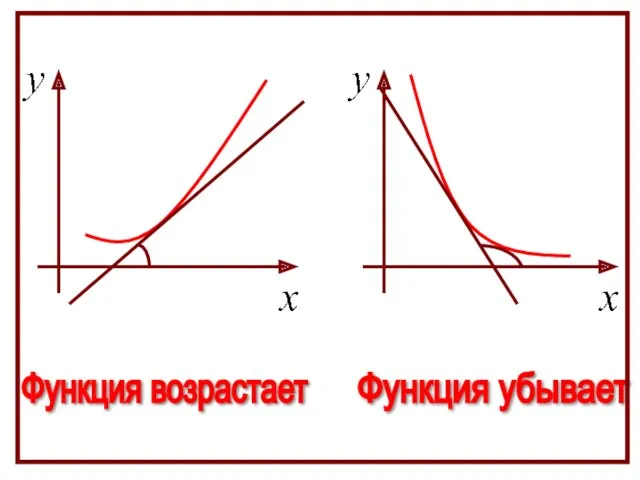
- 5. Геометрическая интерпретация Если касательные к кривой на некотором промежутке направлены под острыми углами к оси х,
- 6. Функция возрастает Функция убывает
- 7. Пример. Найти интервалы монотонности функции
- 8. Решение: Найдем производную этой функции: Исследуем знак этой производной: Следовательно, функция будет возрастать на промежутке Функция
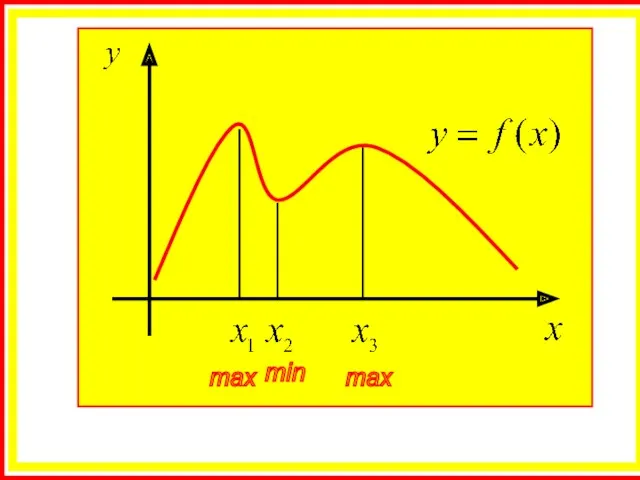
- 9. Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х0 выполняется неравенство 2.
- 10. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство Значения
- 11. max min max
- 12. На одном промежутке функция может иметь несколько экстремумов, причем может быть, что минимум в одной точке
- 13. Однако, функция может иметь экстремум в точке, в которой она не дифференцируема. Например, функция имеет минимум
- 14. Для того, чтобы функция y=f(x) имела экстремум в точке х0 , необходимо, чтобы ее производная в
- 15. Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными. Т.об., если в какой-либо точке
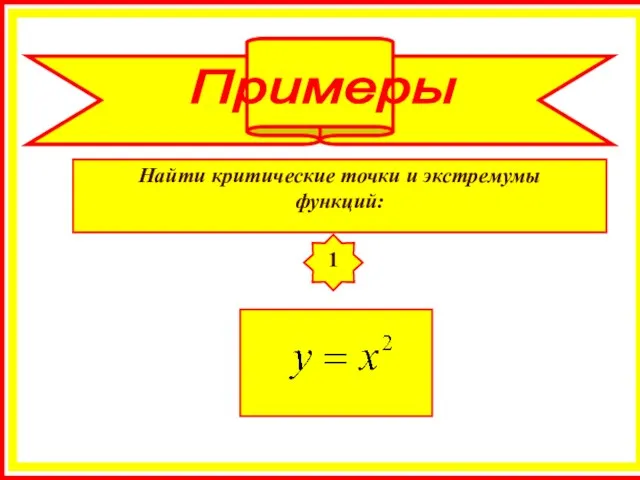
- 16. Найти критические точки и экстремумы функций: 1 Примеры
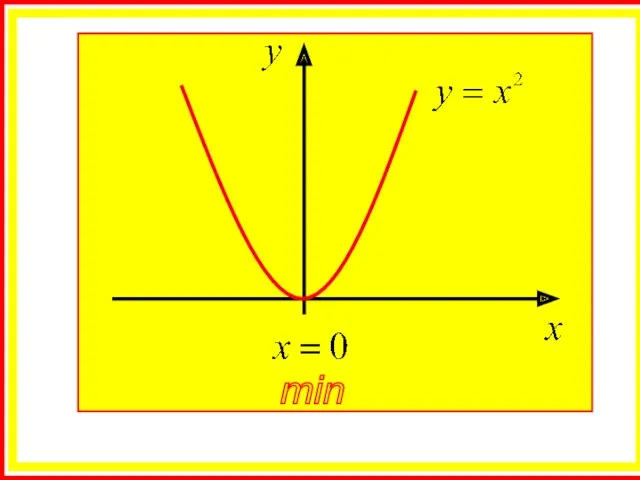
- 17. Решение: Применим необходимое условие экстремума: - критическая точка
- 18. min
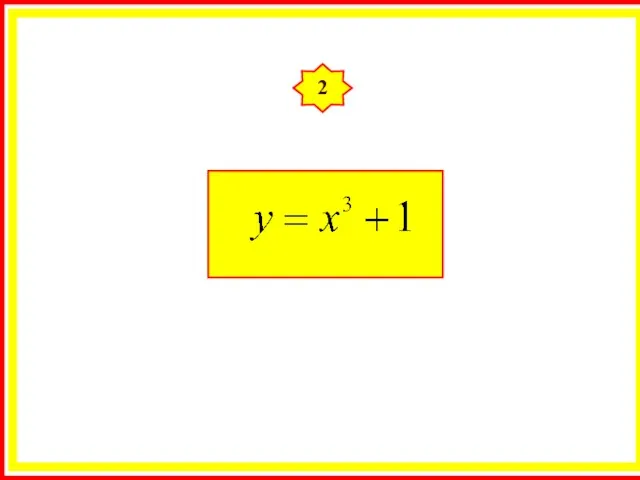
- 19. 2
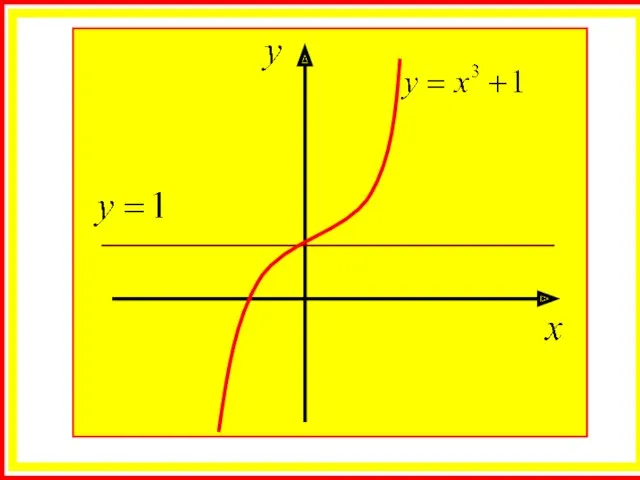
- 20. Решение: Применим необходимое условие экстремума: - критическая точка
- 22. Если при переходе через точку х0 производная дифференцируемой функции y=f(x)меняет знак с плюса на минус, то
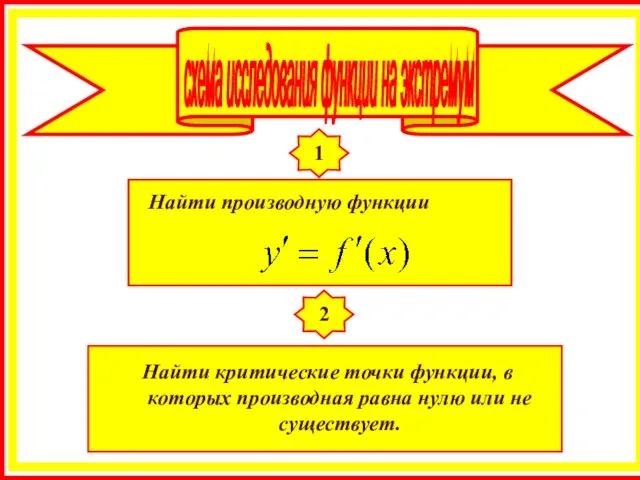
- 23. 1 Найти производную функции 2 Найти критические точки функции, в которых производная равна нулю или не
- 24. 3 Исследовать знак производной слева и справа от каждой критической точки. 4 Найти экстремум функции.
- 25. Исследовать функцию на экстремум: Пример
- 26. Решение: Применим схему исследования функции на экстремум: 1 Находим производную функции:
- 27. 2 Находим критические точки: критические точки
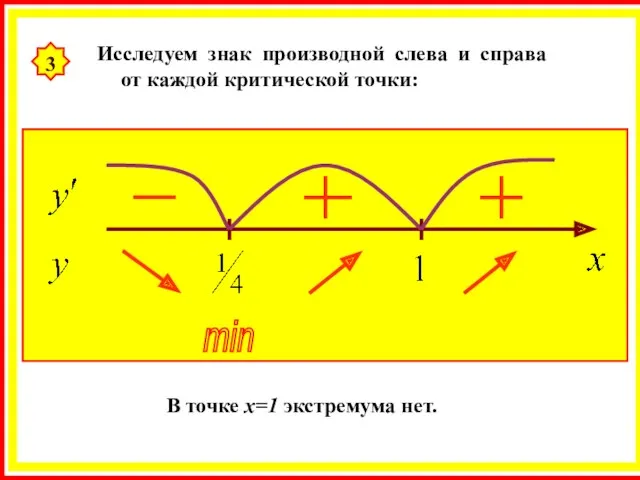
- 28. 3 Исследуем знак производной слева и справа от каждой критической точки: min В точке х=1 экстремума
- 29. 4 Находим экстремум функции:
- 30. Согласно теореме Вейерштрасса, если функция непрерывна на отрезке [a;b], то она достигает на нем наибольшего и
- 31. схема нахождения наибольшего и наименьшего значения функции на отрезке: 1 Найти производную функции.
- 32. 2 Найти критические точки, в которых производная равна нулю или не существует. 3 Найти значения функции
- 33. пример. Найти наибольшее и наименьшее значения функции на отрезке
- 34. решение: 1 Находим производную функции: 2 Находим критические точки: критические точки
- 35. 3 Находим значения функций в критических точках и на концах отрезка:
- 36. ЗАМЕЧАНИЕ Если функция непрерывна на интервале (а;в), то она может не принимать на нем наибольшее и
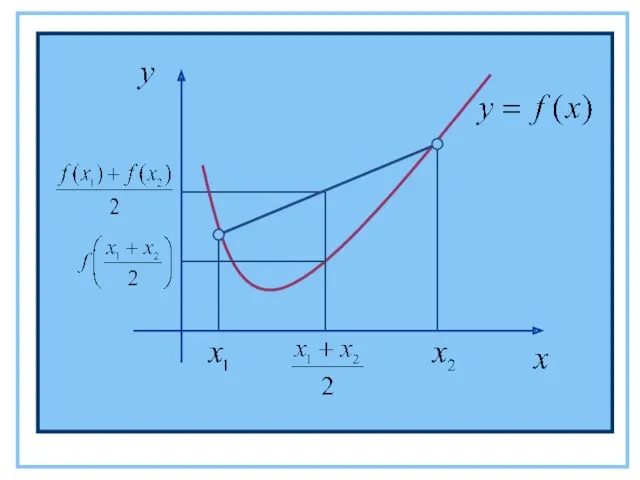
- 37. Функция y=f(x) называется выпуклой вниз (вогнутой) на промежутке Х, если для любых х1, х2 из этого
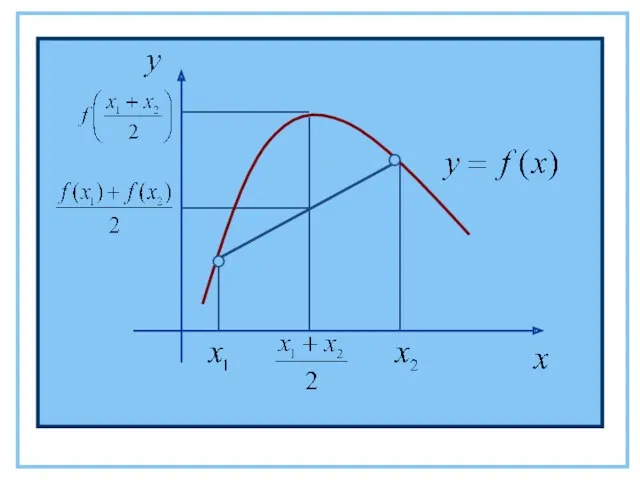
- 39. Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых х1, х2 из этого промежутка
- 41. ТЕОРЕМА 1. Функция выпукла вверх (вниз) на промежутке Х тогда и только тогда, когда ее первая
- 42. ТЕОРЕМА 2. достаточное условие выпуклости функции Если вторая производная дифференцируемой функции положительна (отрицательна) на некотором промежутке
- 43. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, на которых функция выпукла вверх и вниз.
- 44. ТЕОРЕМА 3. необходимое условие перегиба Вторая производная дифференцируемой функции в точке перегиба х0 равна нулю:
- 45. ТЕОРЕМА 4. достаточное условие перегиба Если вторая производная дифференцируемой функции в точке х0 меняет свой знак,
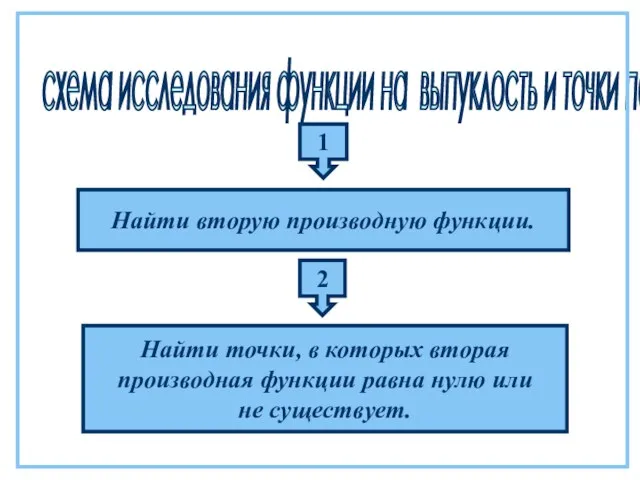
- 46. схема исследования функции на выпуклость и точки перегиба: 1 Найти вторую производную функции. 2 Найти точки,
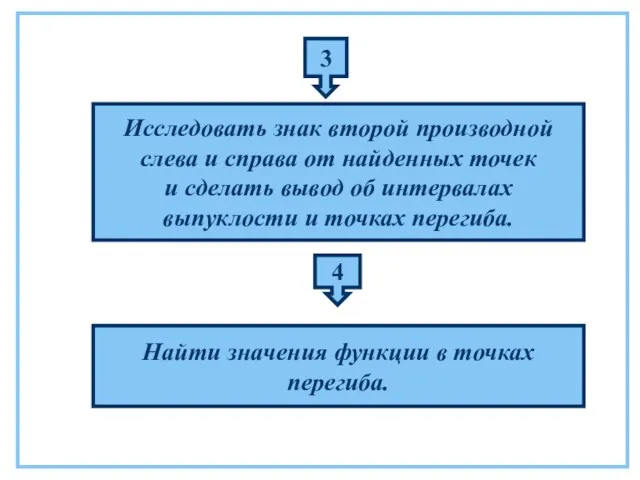
- 47. 3 Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах
- 48. Пример. Найти интервалы выпуклости и точки перегиба функции
- 49. Решение: 1 Находим вторую производную: 2 Находим точки, в которых вторая производная обращается в нуль:
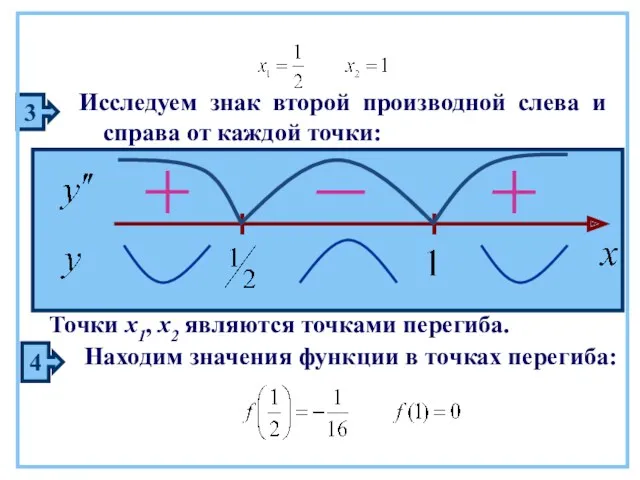
- 50. 3 Исследуем знак второй производной слева и справа от каждой точки: Точки х1, х2 являются точками
- 51. Асимптотой графика функции y=f(x) называется прямая, такая что расстояние от точки (x,f(x)) до этой прямой стремиться
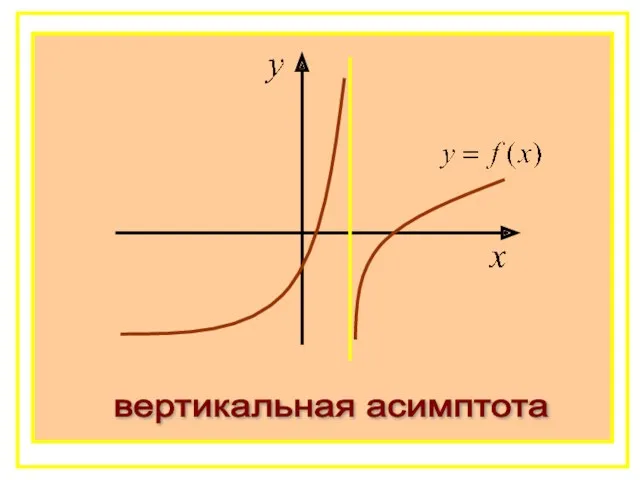
- 52. вертикальная асимптота
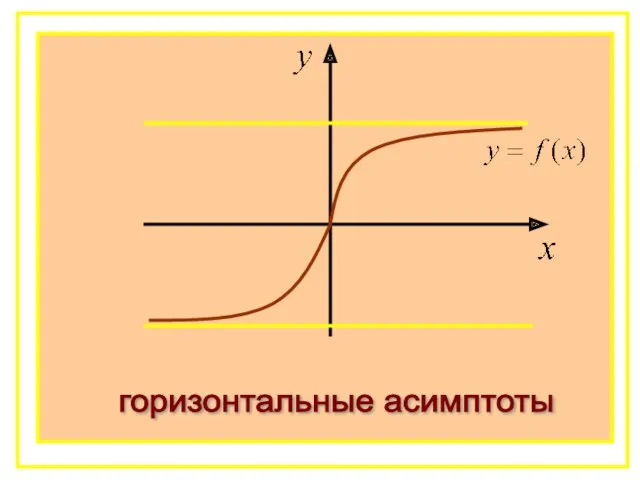
- 53. горизонтальные асимптоты
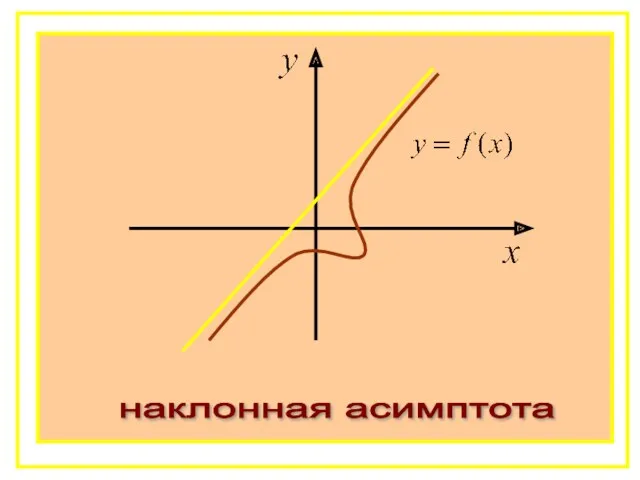
- 54. наклонная асимптота
- 55. ТЕОРЕМА 1. Пусть функция y=f(x) определена в некоторой окрестности точки х0 (исключая, может быть, саму эту
- 56. Тогда прямая х=х0 является вертикальной асимптотой графика функции y=f(x). или
- 57. Очевидно, что прямая х=х0 не может быть вертикальной асимптотой, если функция непрерывна в точке х0, т.к.
- 58. ТЕОРЕМА 2. Пусть функция y=f(x) определена при достаточно больших х и существует конечный предел функции Тогда
- 59. ТЕОРЕМА 3. Пусть функция y=f(x) определена при достаточно больших х и существуют конечные пределы Тогда прямая
- 60. Пример. Найти асимптоты графика функции
- 61. Решение: Функция не имеет точек разрыва, следовательно вертикальных асимптот у нее нет. 1 2 Найдем горизонтальные
- 62. Следовательно, прямая является наклонной асимптотой.
- 63. 1 Найти область определения функции. 2 Исследовать функцию на четность и периодичность. Схема исследования функции и
- 64. 3 Найти вертикальные асимптоты. 4 Исследовать поведение функции на бесконечности и найти горизонтальные или наклонные асимптоты.
- 65. 6 Найти интервалы выпуклости функции и точки перегиба. 7 Найти точки пересечения графика с осями координат
- 66. Пример. Исследовать функцию и построить ее график
- 67. Решение: 1 Находим область определения функции. Функция определена при всех значениях х, кроме Следовательно, область определения
- 68. Функция является четной, следовательно ее график будет симметричен относительно оси ординат. Функция не периодична. 3 Находим
- 69. При слева При справа Следовательно, прямая х=1 является вертикальной асимптотой. Аналогично можно проанализировать х=-1, но так
- 70. Следовательно, y=-1 - горизонтальная асимптота. Т.к. то наклонных асимптот нет. 5 Найдем интервалы монотонности и экстремумы
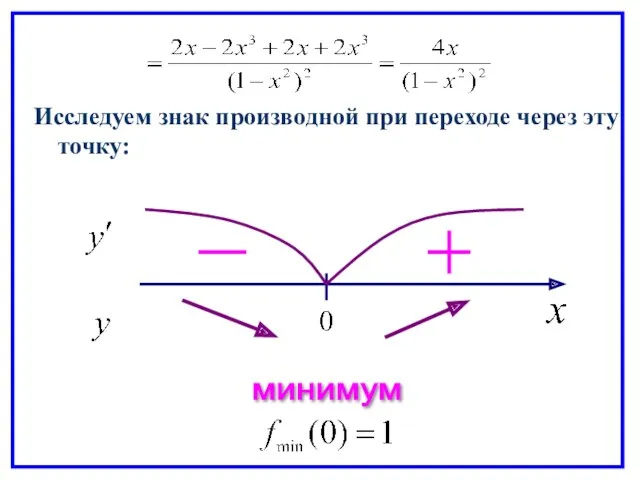
- 71. Исследуем знак производной при переходе через эту точку: минимум
- 72. Интервалы монотонности функции: Функция убывает на: Функция возрастает на: 6 Найдем интервалы выпуклости и точки перегиба.
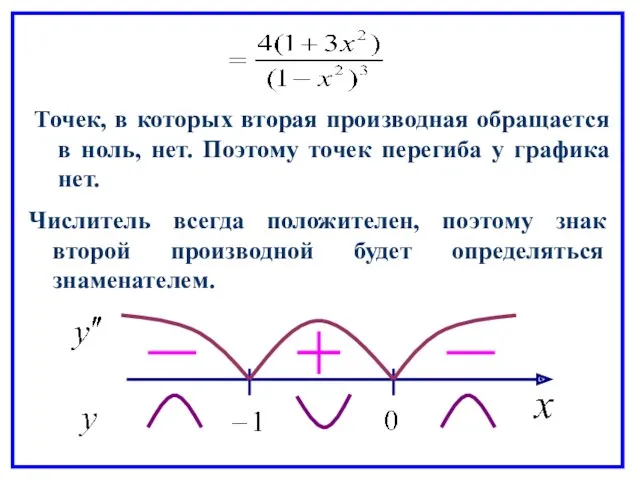
- 73. Точек, в которых вторая производная обращается в ноль, нет. Поэтому точек перегиба у графика нет. Числитель
- 74. Интервалы выпуклости функции: Функция выпукла вниз на: Функция выпукла вверх на: 7 Найдем точки пересечения графика
- 76. Скачать презентацию



















![Согласно теореме Вейерштрасса, если функция непрерывна на отрезке [a;b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/416958/slide-29.jpg)




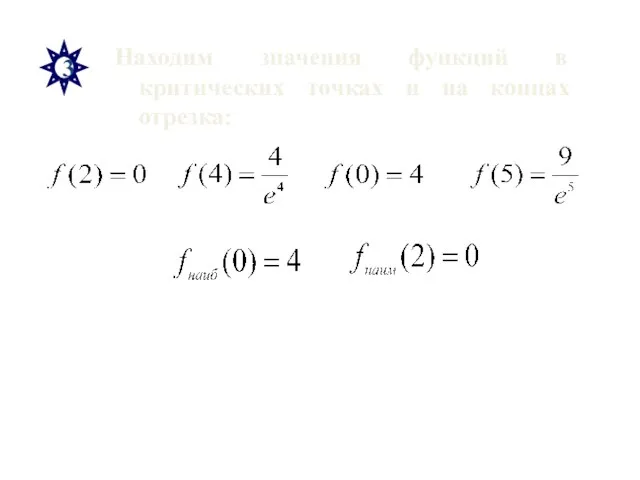




























 Выполнение моделей простых форм (куб, конус, цилиндр)
Выполнение моделей простых форм (куб, конус, цилиндр) Пирамида. Строение пирамиды
Пирамида. Строение пирамиды Логарифмы и их свойства
Логарифмы и их свойства Аксиомы стереомотрии
Аксиомы стереомотрии The discoveries of Pythagoras
The discoveries of Pythagoras Сложение чисел с разными знаками. 6 класс
Сложение чисел с разными знаками. 6 класс Площадь. Многоугольник
Площадь. Многоугольник Общие сведение о метрологии
Общие сведение о метрологии Объемы тел. 11 класс
Объемы тел. 11 класс Комбинаторика. Размещения и сочетания. Дискретный анализ. Лекция 4
Комбинаторика. Размещения и сочетания. Дискретный анализ. Лекция 4 Средства измерений, их классификация
Средства измерений, их классификация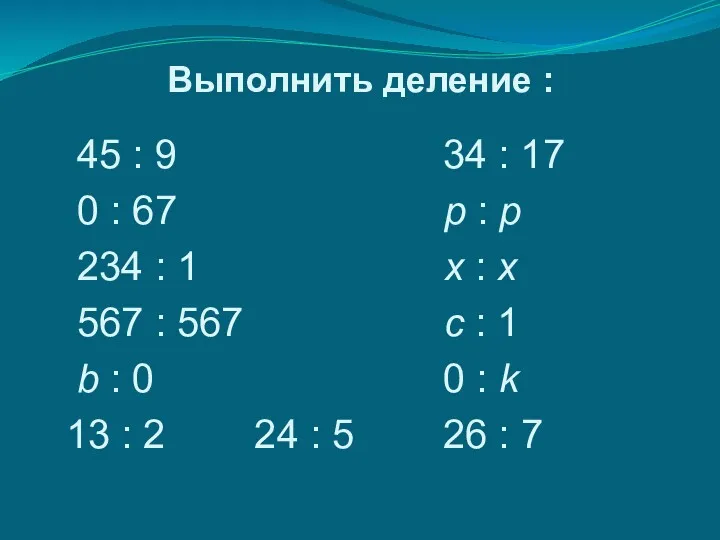 Деление с остатком
Деление с остатком Объем шара
Объем шара Вычитание чисел. Задачи
Вычитание чисел. Задачи Меры длины. Закрепление.
Меры длины. Закрепление. 20230930_ponyatie_polozhitelnoy_desyatichnoy_drobi
20230930_ponyatie_polozhitelnoy_desyatichnoy_drobi Скалярное произведение векторов в координатах
Скалярное произведение векторов в координатах Презентации по математике
Презентации по математике Корень уравнения. Правила решения уравнений
Корень уравнения. Правила решения уравнений Решение задач на перпендикулярность прямой и плоскости. (10 класс)
Решение задач на перпендикулярность прямой и плоскости. (10 класс)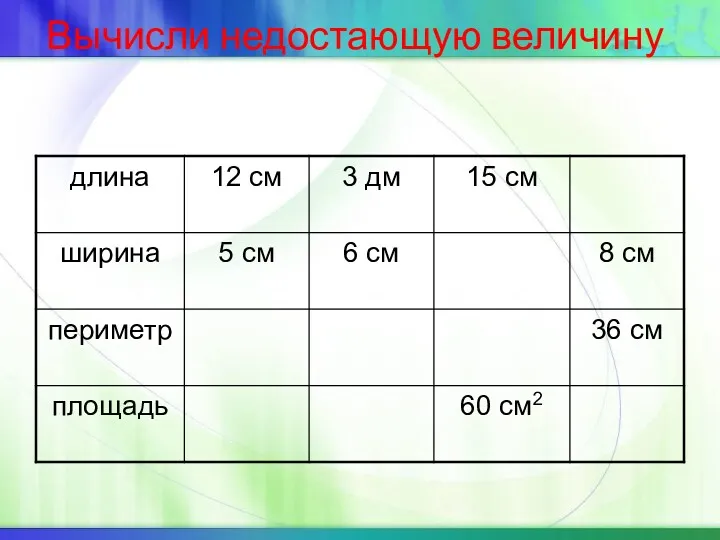 Площадь прямоугольника
Площадь прямоугольника Функция, ее область определения и множество значений. График функции
Функция, ее область определения и множество значений. График функции Десятичная запись числа
Десятичная запись числа Математическая игра 4класс Величины. Своя игра
Математическая игра 4класс Величины. Своя игра Равенство треугольников. Второй признак равенства треугольников
Равенство треугольников. Второй признак равенства треугольников Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Основы теории вероятностей. Основные понятия и определения
Основы теории вероятностей. Основные понятия и определения Пересечение поверхностей. (Лекция 7)
Пересечение поверхностей. (Лекция 7)