Содержание
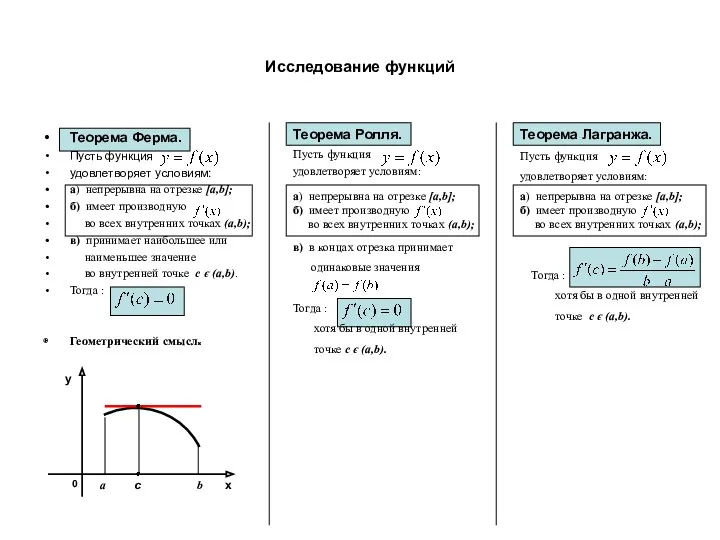
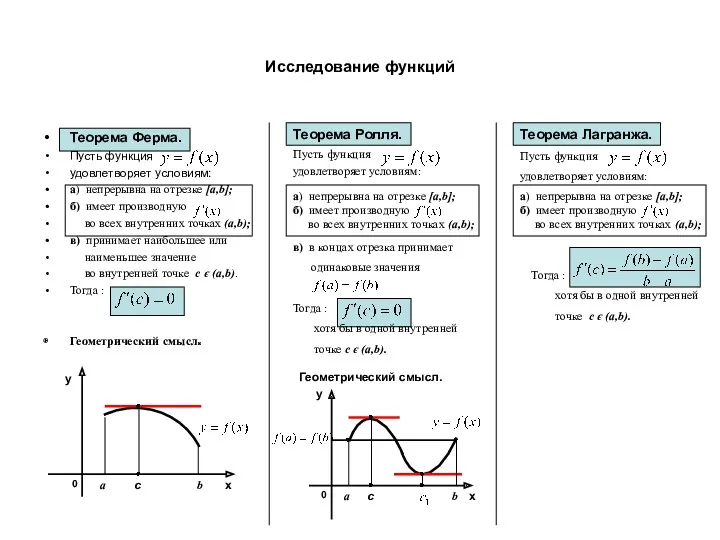
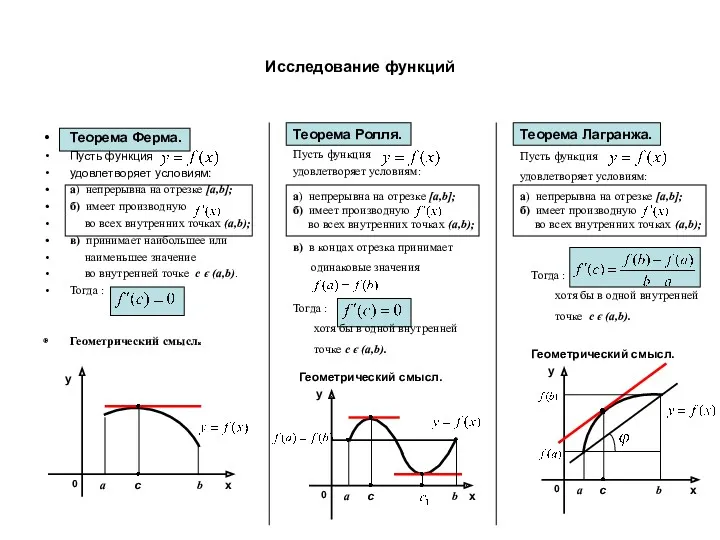
- 2. Исследование функций Теорема Ферма. Теорема Ролля. Теорема Лагранжа.
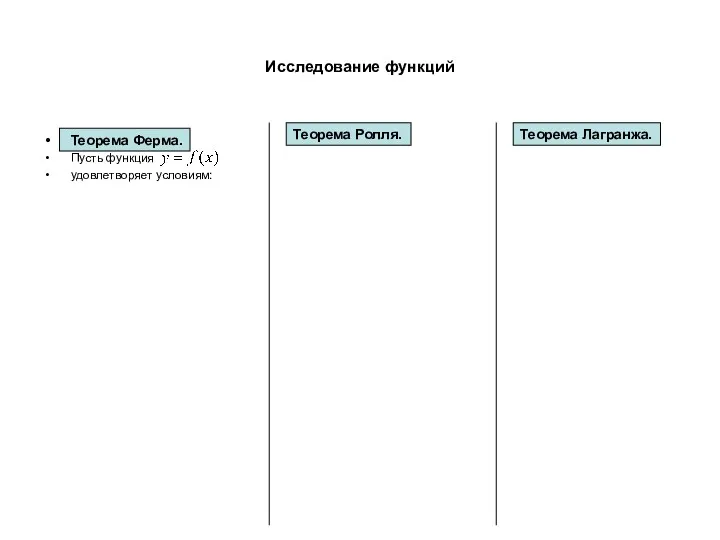
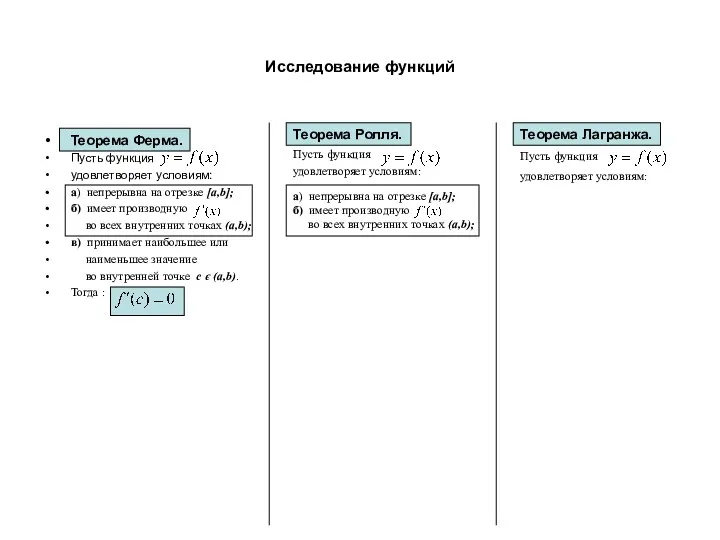
- 3. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: Теорема Ролля. Теорема Лагранжа.
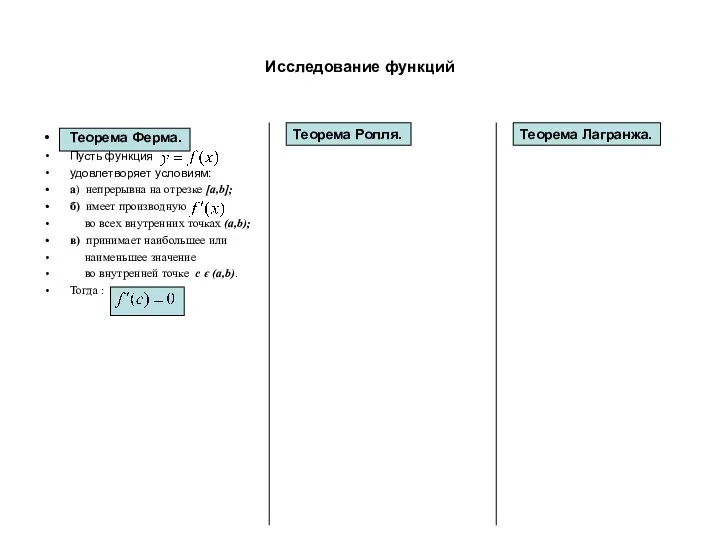
- 4. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
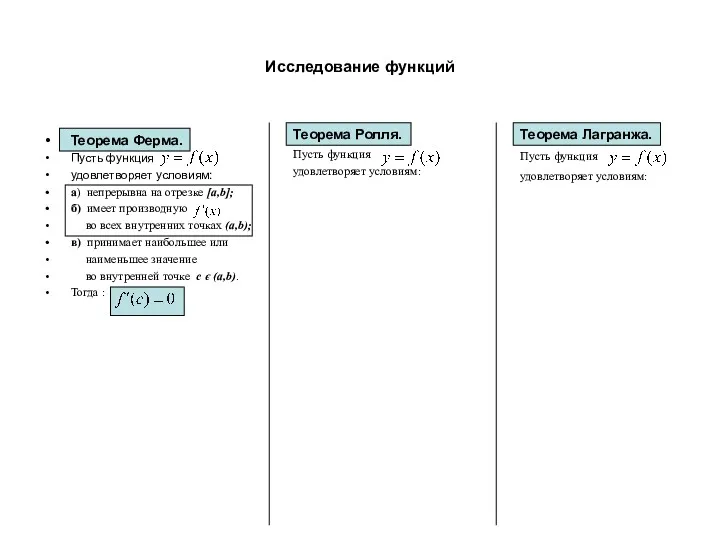
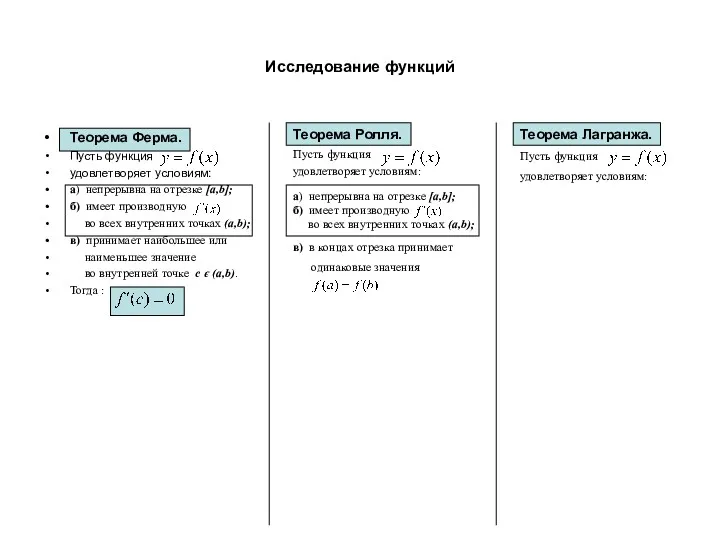
- 5. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
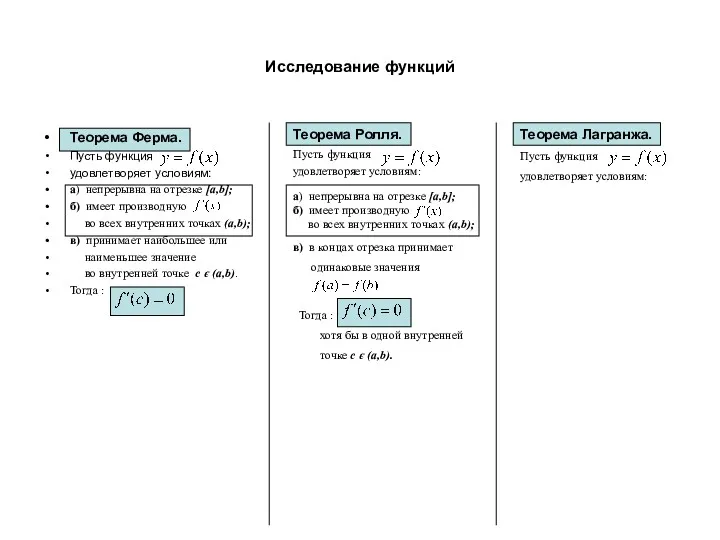
- 6. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
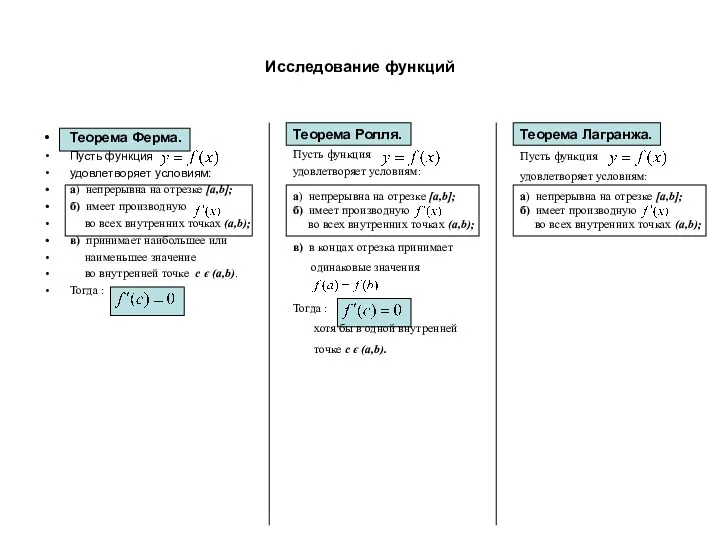
- 7. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
- 8. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
- 9. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
- 10. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
- 11. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
- 12. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
- 13. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: а) непрерывна на отрезке [a,b]; б) имеет производную
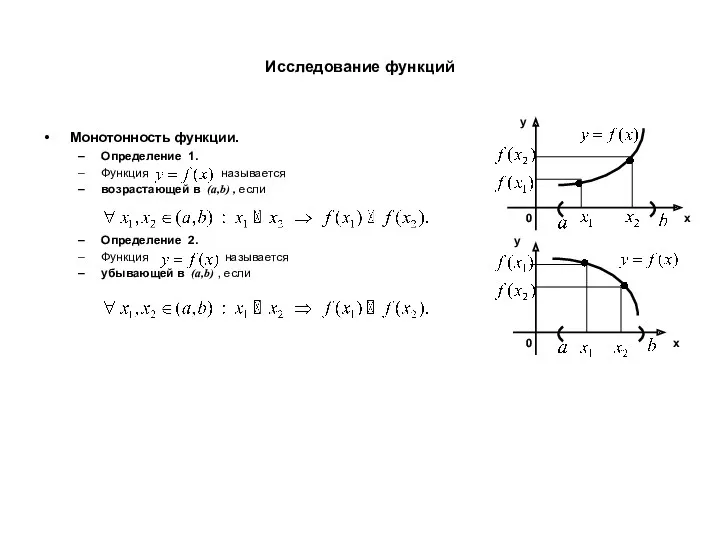
- 14. Исследование функций Монотонность функции. Определение 1. Функция называется возрастающей в (a,b) , если Определение 2. Функция
- 15. Исследование функций Теорема. Пусть Тогда: Доказательство. 1. 2. 3.
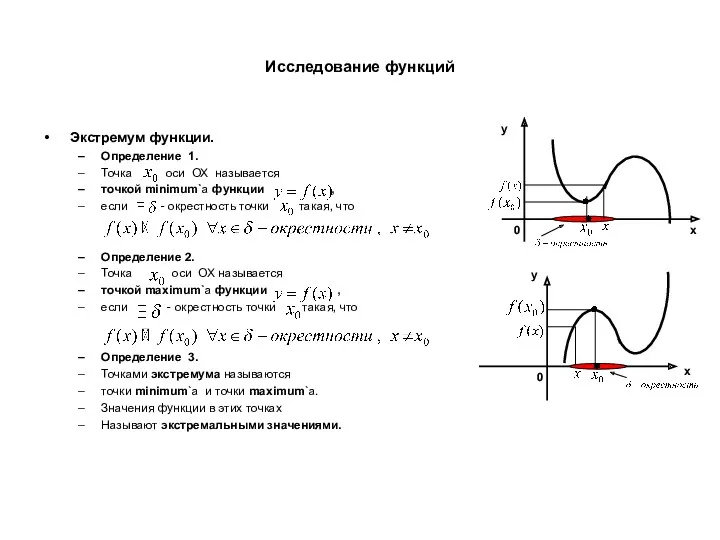
- 16. Исследование функций Экстремум функции. Определение 1. Точка оси ОХ называется точкой minimum`а функции , если -
- 17. Исследование функций Необходимый признак экстремума. Теорема. 1. 2. Доказательство. Пусть - удовлетворяет теореме Ферма Определение 3.
- 18. Исследование функций Достаточные признаки экстремума. Определение. Пусть определена и непрерывна в δ - окрестности точки (включая
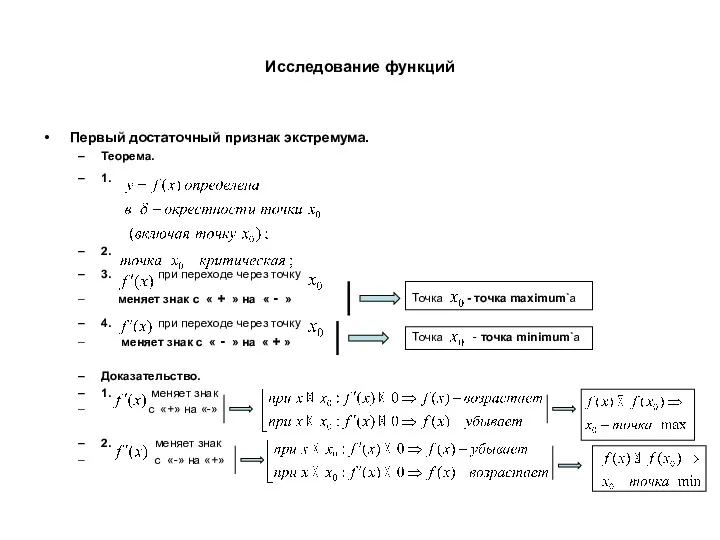
- 19. Исследование функций Первый достаточный признак экстремума. Теорема. 1. 2. 3. при переходе через точку меняет знак
- 20. Исследование функций Второй достаточный признак экстремума. Теорема. 1. 2. 3. 4. Точка - точка minimum`а Точка
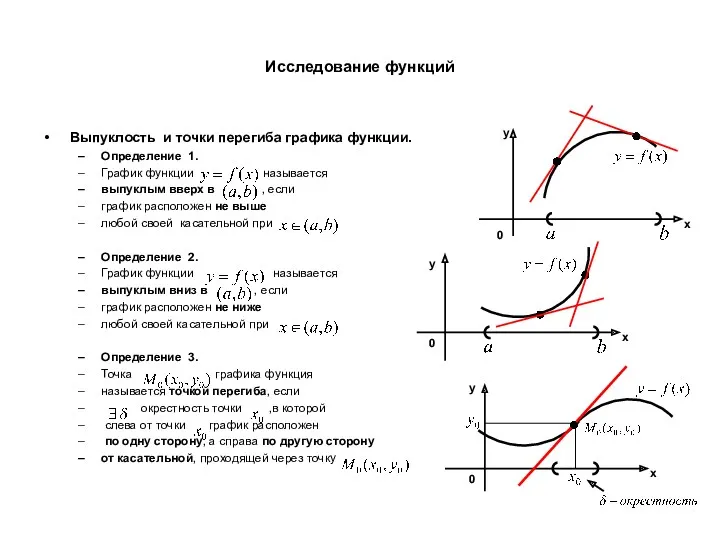
- 21. Исследование функций Выпуклость и точки перегиба графика функции. Определение 1. График функции называется выпуклым вверх в
- 22. Исследование функций Достаточный признак выпуклости. Теорема. 1. 2. 3. График функции выпуклый вниз в График функции
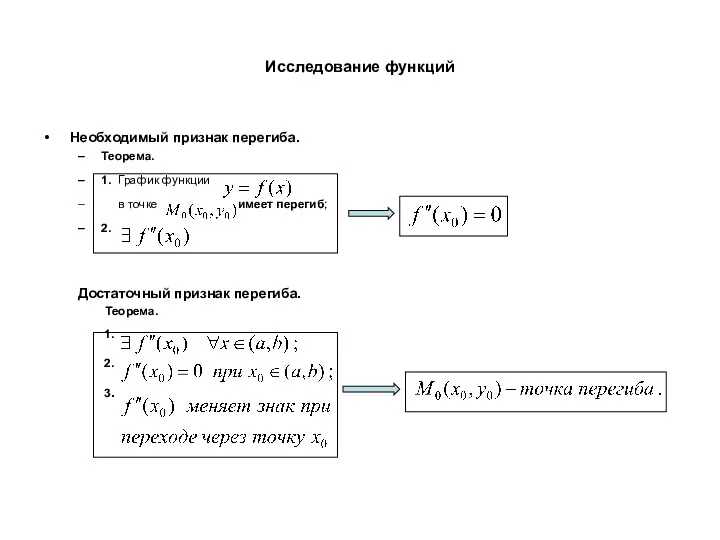
- 23. Исследование функций Необходимый признак перегиба. Теорема. 1. График функции в точке имеет перегиб; 2. Достаточный признак
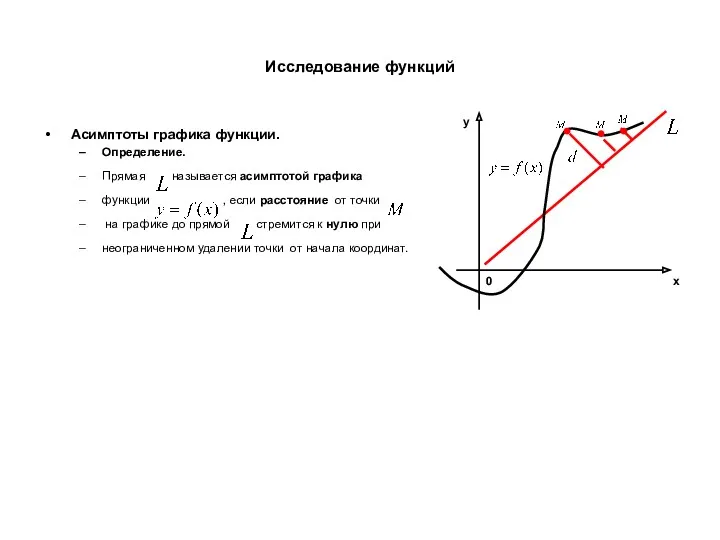
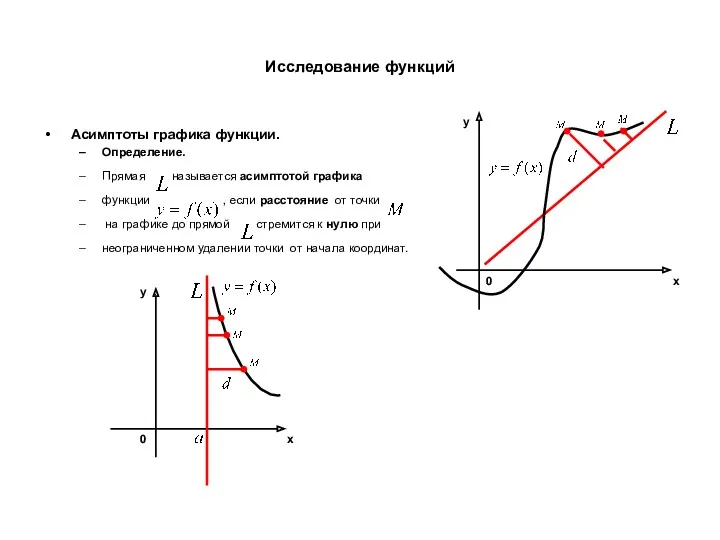
- 24. Исследование функций Асимптоты графика функции. Определение. Прямая называется асимптотой графика функции , если расстояние от точки
- 25. Исследование функций Асимптоты графика функции. Определение. Прямая называется асимптотой графика функции , если расстояние от точки
- 26. Исследование функций Асимптоты графика функции. Определение. Прямая называется асимптотой графика функции , если расстояние от точки
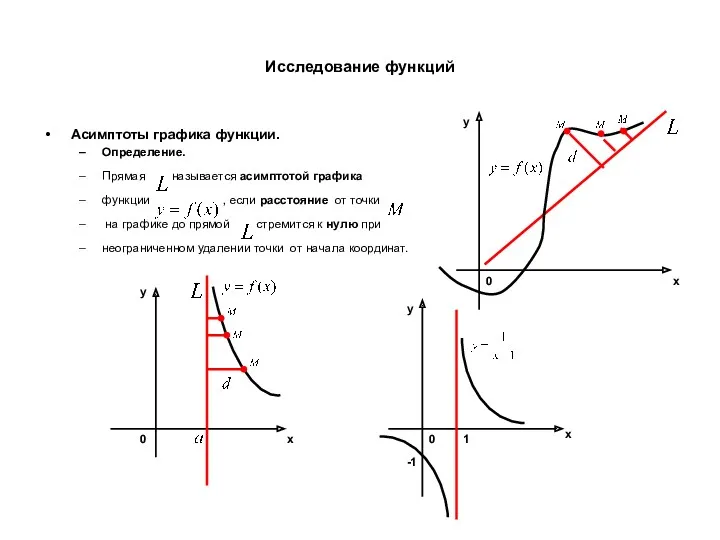
- 27. Исследование функций Теорема 1. Прямая является вертикальной асимптотой, если хотя бы один из пределов равен Теорема
- 28. Исследование функций Общая схема исследования функции. Первый этап. 1. Область определения, точки разрыва. 2. Четность, нечетность.
- 29. Исследование функций Пример 1. Исследовать функцию и построить график 1. О.О.Ф. 2. Четность, нечетность: 3. Непериодическая.
- 30. Исследование функций 5. Асимптоты. а) вертикальных асимптот нет; б) наклонные: 6. Поведение при Наклонных асимптот нет
- 31. Исследование функций Исследование с помощью первой производной.
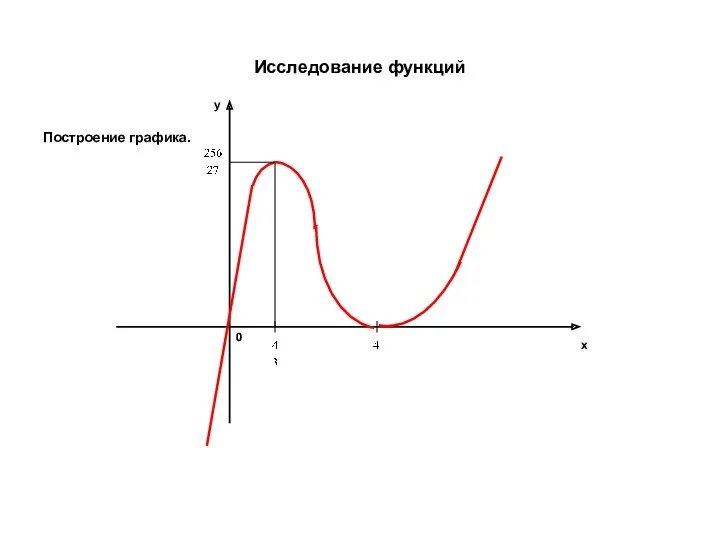
- 32. Исследование функций Построение графика. x y 0
- 33. Исследование функций Исследование с помощью второй производной. х + -
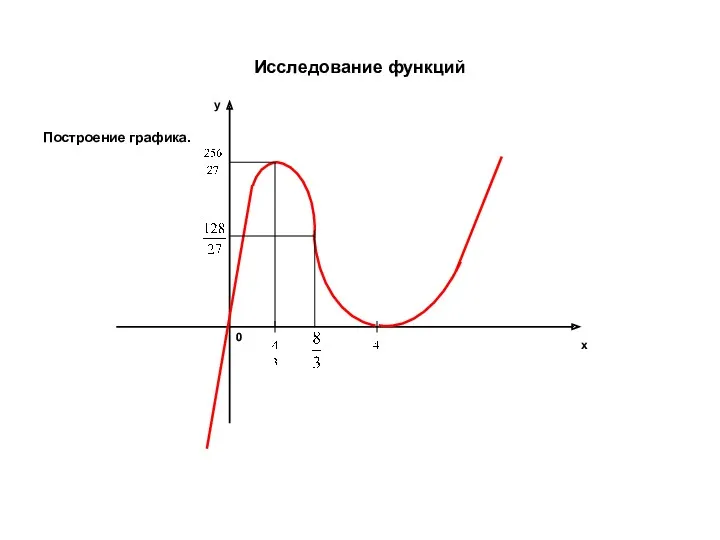
- 34. Исследование функций Построение графика. x y 0
- 35. Исследование функций Пример 2. Исследовать функцию и построить график . 1. О.О.Ф.: 2. Четность, нечетность: 3.
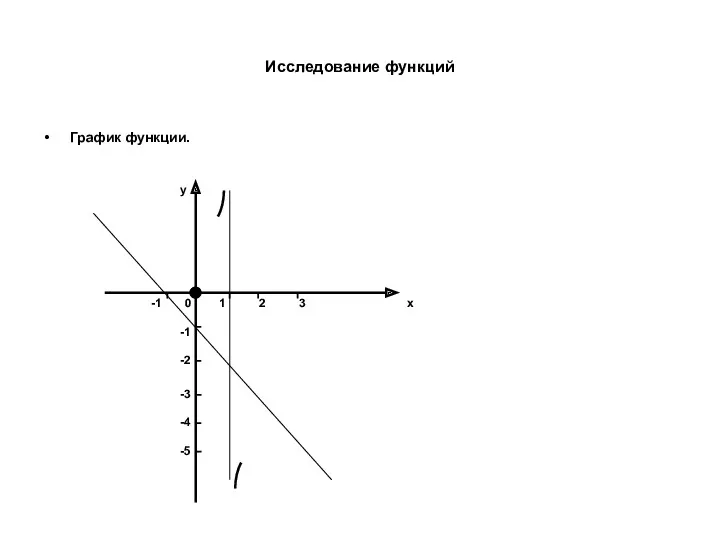
- 36. Исследование функций График функции. 0 x y 1 2 -1 -1 -3 -2 -4 -5 3
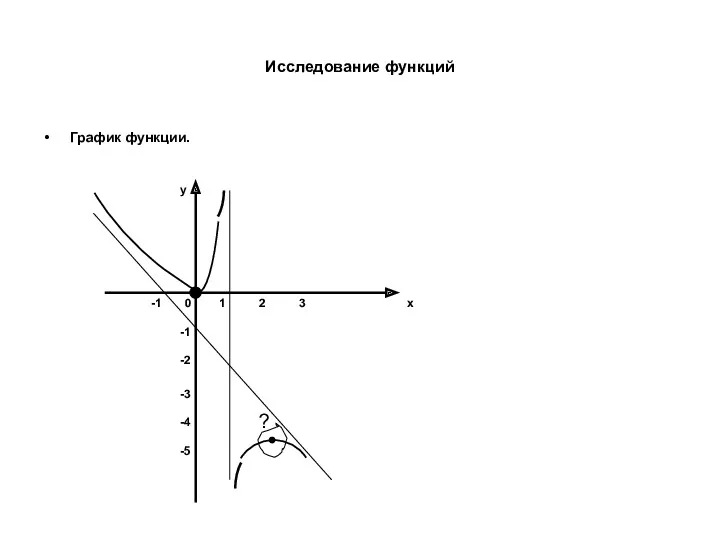
- 37. Исследование функций График функции. ? x y 0 1 2 3 -1 -1 -2 -3 -4
- 38. Исследование функций Исследование с помощью первой производной. x 0 1 2
- 40. Скачать презентацию














 Путешествие в страну геометрических фигур
Путешествие в страну геометрических фигур Задача 3. Определение оптимальных размеров здания по минимуму теплопотерь
Задача 3. Определение оптимальных размеров здания по минимуму теплопотерь Задачи на движение
Задачи на движение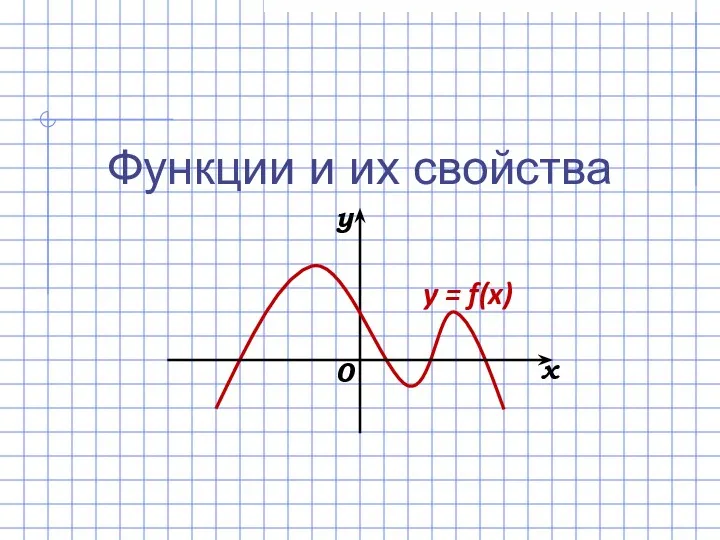 Функции и их свойства
Функции и их свойства Числовые последовательности. 9 класс
Числовые последовательности. 9 класс Элементы корреляционного и регрессионного анализа
Элементы корреляционного и регрессионного анализа Измерение отрезков
Измерение отрезков Презентация ФЭМП в свете ФГОС
Презентация ФЭМП в свете ФГОС Площадь параллелограмма, треугольника и трапеции. Урок 17
Площадь параллелограмма, треугольника и трапеции. Урок 17 Математика и спорт. Задачи
Математика и спорт. Задачи Логические задачи
Логические задачи Презентация к КВМ.
Презентация к КВМ. Математический брейн-ринг для учащихся 6 классов
Математический брейн-ринг для учащихся 6 классов Квадратные корни. Арифметический квадратный корень
Квадратные корни. Арифметический квадратный корень Основные понятия теории вероятности. Лекция 1
Основные понятия теории вероятности. Лекция 1 Виды углов
Виды углов Критерии достоверности
Критерии достоверности Функциональные зависимости в курсе алгебры и физики
Функциональные зависимости в курсе алгебры и физики Проектирование индивидуального образовательного маршрута по математике
Проектирование индивидуального образовательного маршрута по математике Арифметическая и геометрическая прогрессии. Обобщающий урок
Арифметическая и геометрическая прогрессии. Обобщающий урок Неопределенный интеграл, его свойства и вычисление
Неопределенный интеграл, его свойства и вычисление Решение геометрических задач первой части ОГЭ
Решение геометрических задач первой части ОГЭ Сколько в пуде, соли. Познавательное чтение
Сколько в пуде, соли. Познавательное чтение Интерактивный тест для проведения контрольного среза за 1 четверть в 6 классе по учебнику Н.Я.Виленкин
Интерактивный тест для проведения контрольного среза за 1 четверть в 6 классе по учебнику Н.Я.Виленкин Додавання і віднімання числа частинами
Додавання і віднімання числа частинами Первый признак равенства треугольников
Первый признак равенства треугольников Умножение. Переместительное свойство умножения. Закрепление. Математика. 5 класс
Умножение. Переместительное свойство умножения. Закрепление. Математика. 5 класс Статистические ряды распределения и их виды
Статистические ряды распределения и их виды