Содержание
- 2. РЕБУС «СОБЫТИЕ»
- 3. СОБЫТИЕ Под СОБЫТИЕМ понимается явление, которое происходит в результате осуществления какого-либо определенного комплекса условий. ПРИМЕР. Бросаем
- 4. Эксперимент (опыт) ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за объектами или явлениями в строго определенных условиях
- 5. ПРИМЕРЫ сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, химический эксперимент, и
- 6. СТАТИСТИЧЕСКИЙ Эксперимент называют СТАТИСТИЧЕСКИМ, если он может быть повторен в практически неизменных условиях неограниченное число раз.
- 7. СЛУЧАЙНОЕ СОБЫТИЕ СЛУЧАЙНЫМ называют событие, которое может произойти или не произойти в результате некоторого испытания (опыта).
- 8. Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов.
- 9. Опыт 1: Подбрасывание монеты. Испытание – подбрасывание монеты; события – монета упала «орлом» или «решкой». ✔
- 10. Опыт 2: Подбрасывание кубика. Это следующий по популярности после монеты случайный эксперимент. Испытание – подбрасывание кубика;
- 11. Опыт 3: Выбор перчаток. В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются
- 12. Типы событий ДОСТОВЕРНОЕ НЕВОЗМОЖНОЕ СЛУЧАЙНОЕ
- 13. Типы событий Событие называется невозможным, если оно не может произойти в результате данного испытания. Случайным называют
- 14. Примеры событий досто- верные слу- чайные невоз- можные 1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА. 2. ПОСЛЕ НОЧИ
- 15. Охарактеризуйте события, о которых идет речь в приведенных заданиях как достоверные, невозможные или случайные. Петя задумал
- 16. Задание 2 В мешках лежит 10 шаров: 3 синих, 3 белых и 4 красных. Охарактеризуйте следующее
- 17. ИСХОД ИСХОДОМ (или элементарным исходом, элементарным событием) называется один из взаимоисключающих друг друга вариантов, которым может
- 18. Число возможных исходов в каждом из рассмотренных выше опытах. Опыт 1. – 2 исхода: «орел», «решка».
- 19. Однозначные исходы предполагают единственный результат того или иного события: смена дня и ночи, смена времени года
- 20. Неоднозначные исходы предполагают несколько различных результатов того или иного события: при подбрасывании кубика выпадают разные грани;
- 21. Запишите множество исходов для следующих испытаний. а) В урне четыре шара с номерами два, три, пять,
- 22. Основные элементы комбинаторики Размещение Это любое упорядоченное подмножество m из элементов множества n. (Порядок важен). 2.
- 23. Основные элементы комбинаторики Задача.1. Сколько можно записать четырехзначных чисел, используя без повторения все 10 цифр? Решение:
- 24. Задача.2. Пусть имеется множество, содержащие 4 буквы: {А,В,С,Д}. Записать все возможные сочетания из указанных букв по
- 25. Задача.3. Сколькими способами можно расставить 9 различных книг на полке, чтобы определенные 4 книги стояли рядом?
- 26. Ошибка Даламбера. Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой
- 27. Ошибка Даламбера. Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и
- 28. Опыт «Выбор перчаток». В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две
- 29. Вывод: Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При
- 30. ПРОБЛЕМНЫЙ ВОПРОС 1: А можно ли вычислить вероятность события с помощью ряда экспериментов?
- 31. Опыт человечества. Вероятность что осень рыжая гораздо выше, чем белая Весь наш жизненный опыт подсказывает, что
- 32. Частота случайного события. Абсолютной частотой случайного события А в серии из N случайных опытов называется число
- 33. Частота случайного события. Относительной частотой случайного события называют отношение числа появлений этого события к общему числу
- 34. Примеры Пример 1. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота
- 35. Примеры Пример 2. За лето на Черноморском побережье было 67 солнечных дней. Какова частота солнечных дней
- 36. ПРОБЛЕМНЫЙ ВОПРОС 2: Может быть, относительную частоту и нужно принять за вероятность?
- 37. Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события
- 38. Проверка Пример. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз, и при этом герб выпал
- 39. Проверка Пример . Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз, причем герб выпал 12012
- 40. Статистическая вероятность Вероятность случайного события приближенно равна частоте этого события, полученной при проведении большого числа случайных
- 41. Два события А и В называют совместными, если они могут произойти одновременно, при одном исходе эксперимента,
- 42. Действия над событиями 1. Суммой нескольких событий называется событие, состоящие в наступлении хотя бы одного из
- 43. Пример. В урне находятся красные, белые и черные шары. Вынимается один шар. Возможные события: А –
- 44. Диаграммы Венна На диаграмме Венна сумму событий можно изобразить так (прямоугольник – изображение множества всех возможных
- 45. Примеры суммы событий: пусть А - идет дождь, а В - идет снег, то (А +
- 46. 2. Произведением нескольких событий называется событие, состоящие в совместном наступлении всех этих событий в результате испытания.
- 47. На диаграмме Венна пересечение (произведение) изображают так: Ω
- 48. пусть А - из урны вытянули белый шар, В - из урны вытянули белый шар, то
- 49. Диаграммы Венна Графические изображения на плоскости соотношений между множествами называются диаграммами Венна.
- 50. Определение Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может
- 51. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь
- 52. Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность
- 53. Вероятность того, что компьютер имеет скрытые дефекты, равна 0,2. На склад поступило 20 компьютеров. Какое событие
- 54. Случайные величины Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то
- 55. Закон распределения случайной величины Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных
- 56. Любое правило (таблица, функция, график) позволяющее находить вероятность произвольных событий, в частности, указывающее вероятности отдельных значений
- 57. Ряд распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в
- 58. Функция распределения случайной величины
- 59. Многоугольник распределения
- 60. Пример В урне 8 шаров, из них 5 белых, остальные черные. Вынимают 3 шара. Найти закон
- 61. Числовые характеристики СВ Характеристики положения: - математическое ожидание -мода -медиана Характеристики рассеяния: -дисперсия -среднеквадратическое отклонения
- 62. Математическое ожидание Свойства МО
- 63. Дисперсия Свойства дисперсии
- 64. Среднеквадратическое отклонение
- 65. Мода и медиана Модой дискретной СВ Х называется ее значение принимаемое с наибольшей вероятностью по сравнению
- 67. Скачать презентацию
 Координаты на прямой
Координаты на прямой Тождественные преобразования тригонометрических выражений. 9 класс
Тождественные преобразования тригонометрических выражений. 9 класс Методы параметрического спектрального анализа. Оценка порядка АР-модели и сравнение оценок СПМ
Методы параметрического спектрального анализа. Оценка порядка АР-модели и сравнение оценок СПМ Геометрическое тело конус
Геометрическое тело конус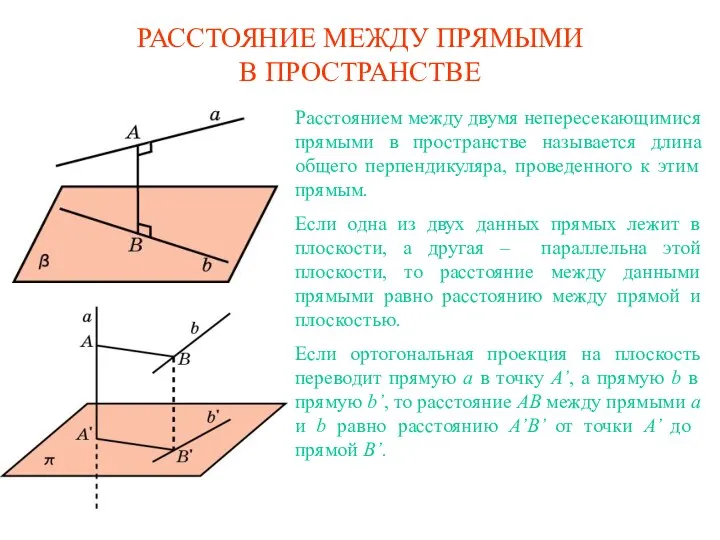 Расстояние между прямыми в пространстве
Расстояние между прямыми в пространстве Линейная функция и ее график. 7 класс
Линейная функция и ее график. 7 класс Статистическая оценка параметров распределений
Статистическая оценка параметров распределений Вычитание вида 11 - …, 12 - …
Вычитание вида 11 - …, 12 - … Кроссворд Параллелепипед
Кроссворд Параллелепипед Решение примеров и задач на сложение и вычитание в пределах 20.
Решение примеров и задач на сложение и вычитание в пределах 20. Действительные числа. 10 класс
Действительные числа. 10 класс Состав чисел первого десятка
Состав чисел первого десятка Решение задний стереометрия(прототипы). Готовимся к ЕГЭ
Решение задний стереометрия(прототипы). Готовимся к ЕГЭ Арифметический квадратный корень
Арифметический квадратный корень Вероятность и статистика. 7 класс
Вероятность и статистика. 7 класс Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Метод математической индукции
Метод математической индукции 7, 8, 0 цифрларын пайдалана отырып, барынша үш таңбалы сандарды жазыңдар
7, 8, 0 цифрларын пайдалана отырып, барынша үш таңбалы сандарды жазыңдар Математический диктант_1 класс
Математический диктант_1 класс Презентация к конспекту занятия по формированию элементарных математических представлений на закрепление изученного материала для детей старшей группы
Презентация к конспекту занятия по формированию элементарных математических представлений на закрепление изученного материала для детей старшей группы Практическое применение теорем геометрии в жизни
Практическое применение теорем геометрии в жизни Определители второго и третьего порядка
Определители второго и третьего порядка Задачи на проценты
Задачи на проценты Части и целое.
Части и целое. Круговая диаграмма
Круговая диаграмма Логарифмические уравнения. Основные методы их решения
Логарифмические уравнения. Основные методы их решения Таблица вариантов. Правило произведения, графы
Таблица вариантов. Правило произведения, графы Все действия с рациональными числами
Все действия с рациональными числами