Содержание
- 2. Признак возрастания (убывания) функции. Критические точки функции – максимумы и минимумы. Правило нахождения интервалов монотонности и
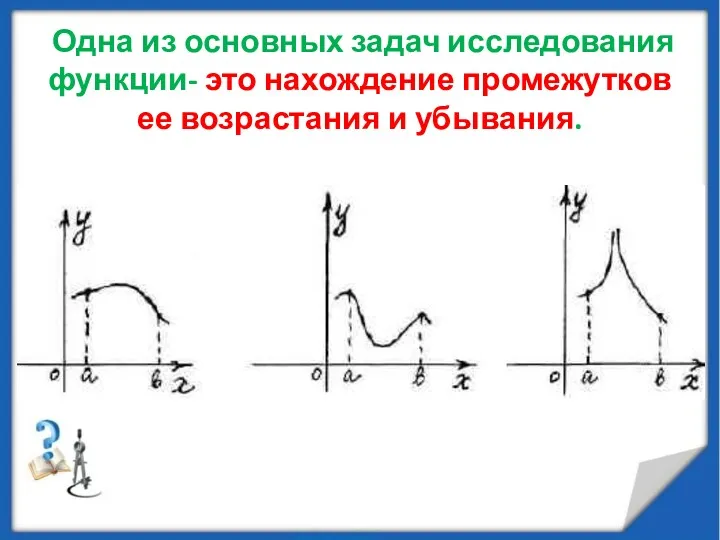
- 3. Одна из основных задач исследования функции- это нахождение промежутков ее возрастания и убывания.
- 4. ОПРЕДЕЛЕНИЕ 1: Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и
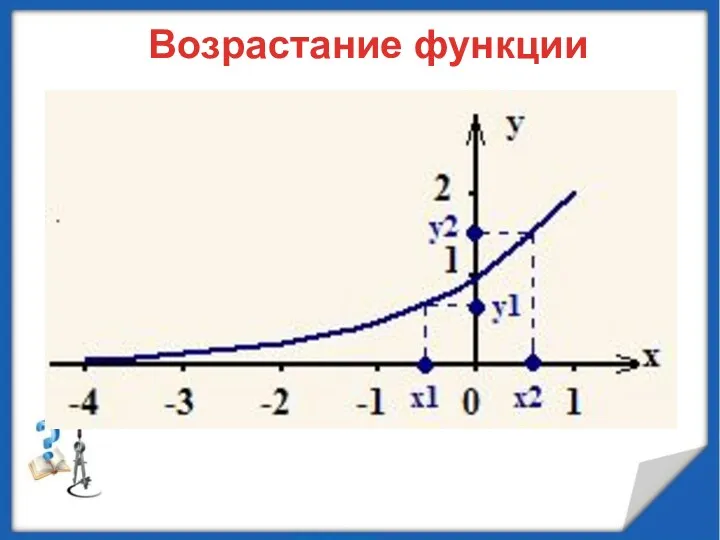
- 5. Возрастание функции
- 6. ОПРЕДЕЛЕНИЕ 2: Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и
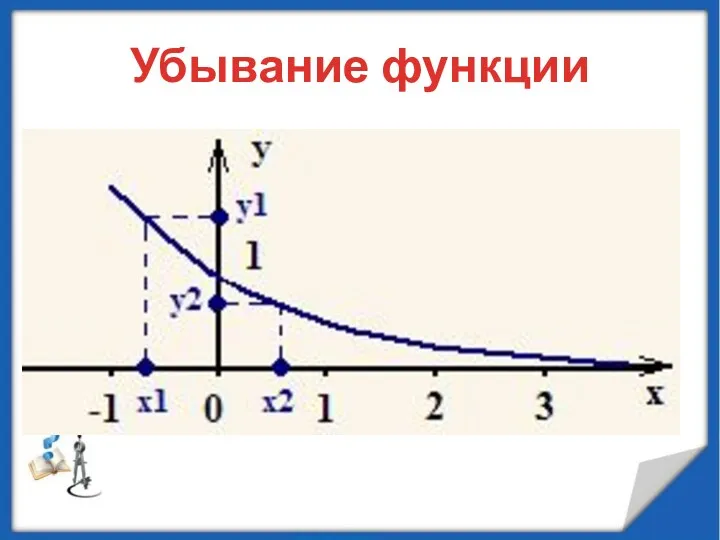
- 7. Убывание функции
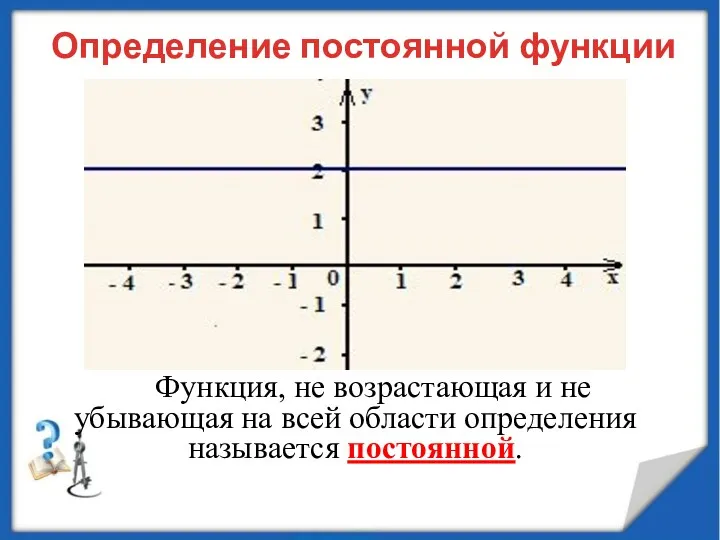
- 8. Определение постоянной функции Функция, не возрастающая и не убывающая на всей области определения называется постоянной.
- 9. Промежутки монотонности Промежутки возрастания и убывания называются промежутками монотонности функции. Если функция возрастает или убывает на
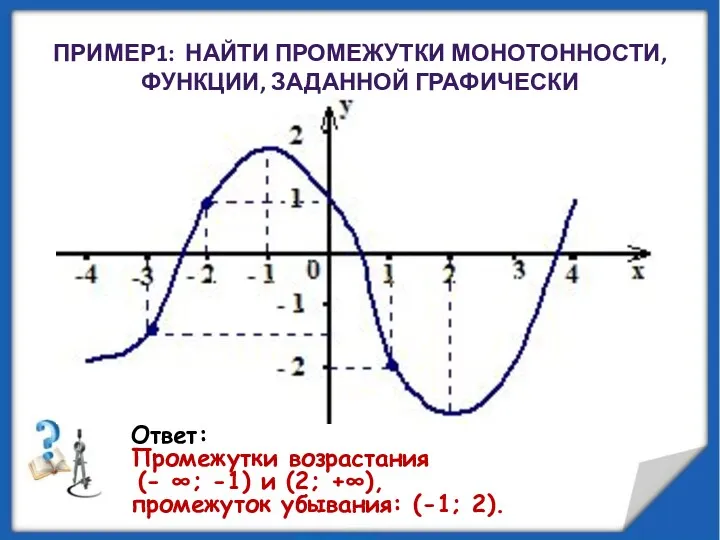
- 10. ПРИМЕР1: НАЙТИ ПРОМЕЖУТКИ МОНОТОННОСТИ, ФУНКЦИИ, ЗАДАННОЙ ГРАФИЧЕСКИ Ответ: Промежутки возрастания (- ∞; -1) и (2; +∞),
- 11. ТЕОРЕМА 1.(необходимые условия возрастания и убывания функции). Если дифференцируемая функция у = f(x), x ∈(а,b) возрастает
- 12. ТЕОРЕМА 2.(достаточный признак возрастания и убывания функций). Если f’(x)>0, в каждой точке интервала (a,b), то функция
- 13. Точки области определения функции, в которых производная функции равна нулю или не существует, называются КРИТИЧЕСКИМИ ТОЧКАМИ.
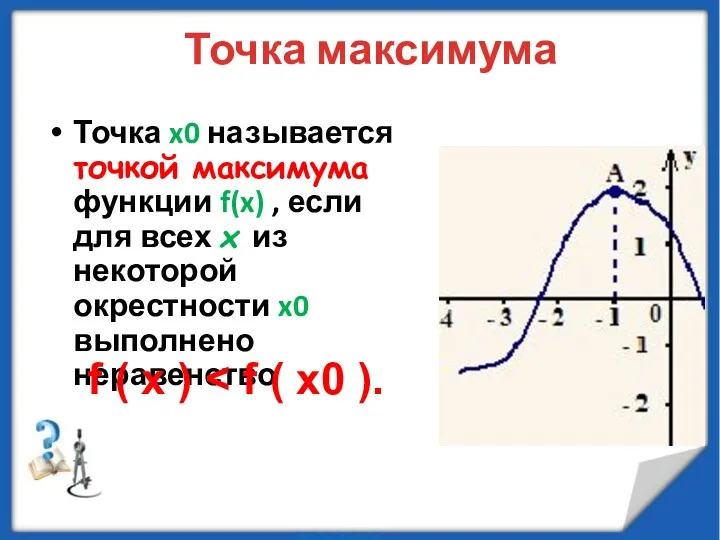
- 14. Точка максимума Точка x0 называется точкой максимума функции f(x) , если для всех x из некоторой
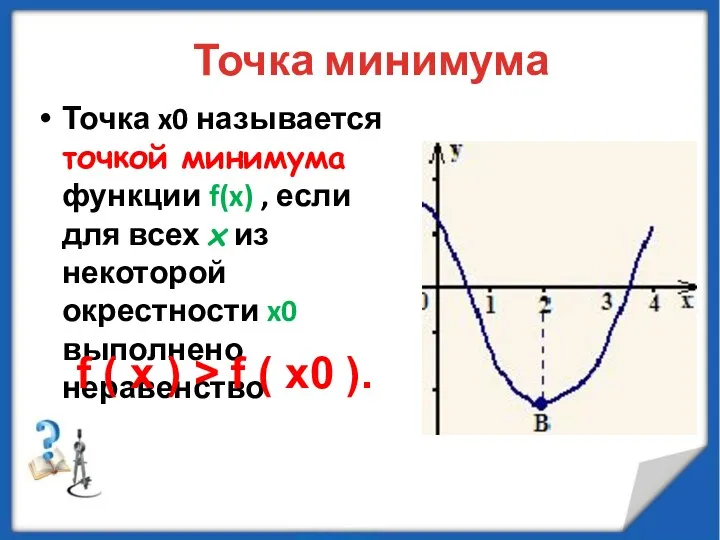
- 15. Точка минимума Точка x0 называется точкой минимума функции f(x) , если для всех x из некоторой
- 16. Точки максимума и минимума функции f(x) называются точками экстремума этой функции, а значения функции в точках
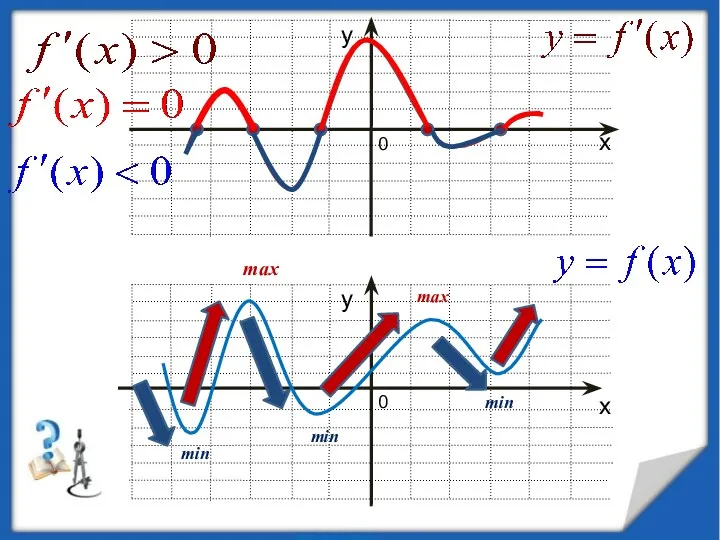
- 17. 0 0 min max min min max
- 18. Экстремум функции, если он существует, может быть только в критических точках. Однако не во всякой критической
- 19. ТЕОРЕМА 3.(необходимое условие экстремума). Теорема Ферма. Если функция у = f(х) имеет экстремум в точке х
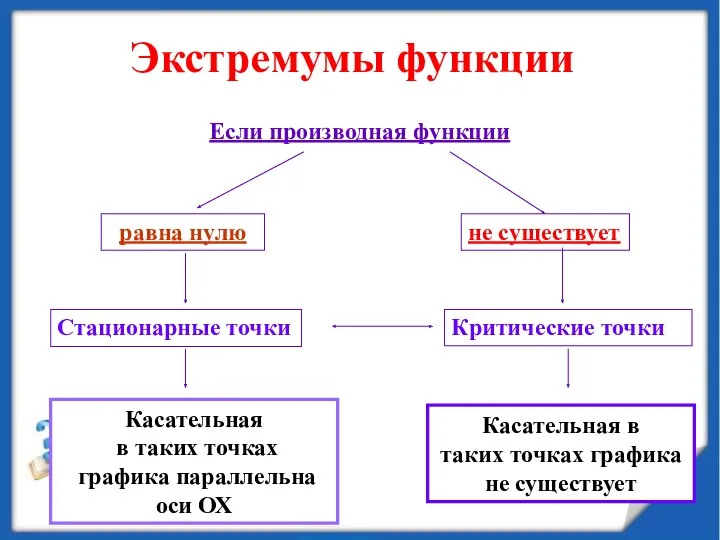
- 20. Экстремумы функции Стационарные точки Критические точки Если производная функции равна нулю не существует Касательная в таких
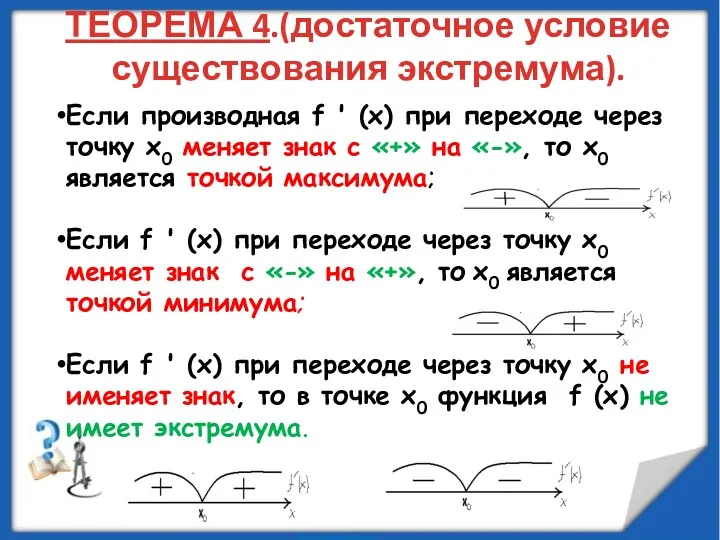
- 21. Если производная f ' (х) при переходе через точку х0 меняет знак с «+» на «-»,
- 22. 1).Найти область определения функции: D(f). 2). Найти f’(x). 3).Найти точки, в которых выполняется равенство f’(x)=0 ?Правило
- 23. 4). Найти точки, в которых выполняется равенство f’(x) не существует. 5).Отметить на координатной прямой все критические
- 24. 7). Сделать выводы о наличии или отсутствии экстремума в каждой из критических точек: если знак производной
- 25. ПРИМЕР . ИССЛЕДОВАТЬ НА ЭКСТРЕМУМ ФУНКЦИЮ У = 2Х3 – 15Х2 + 36Х + 1 1.
- 26. Исследование функций с помощью второй производной 09.09.2020
- 27. 09.09.2020
- 28. Пример. Исследовать функцию на экстремум с помощью 2-ой производной: 09.09.2020 http://aida.ucoz.ru
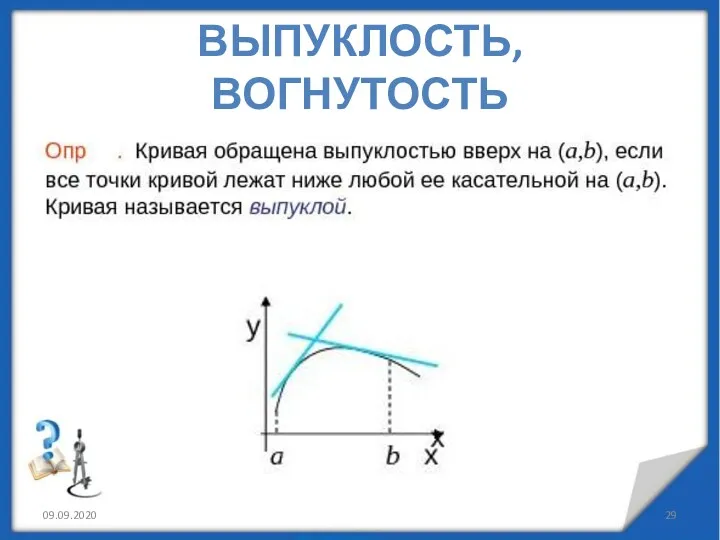
- 29. ВЫПУКЛОСТЬ, ВОГНУТОСТЬ 09.09.2020
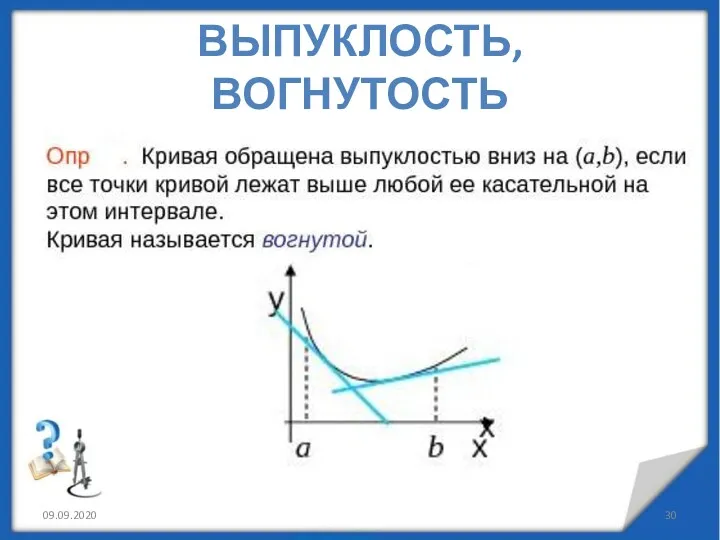
- 30. 09.09.2020 ВЫПУКЛОСТЬ, ВОГНУТОСТЬ
- 31. Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции. Выпуклость
- 32. Пример 09.09.2020
- 33. Пример 2. Найти промежутки выпуклости кривых: f(x)=x⁴ - 2x³ + 6x – 4 Находим: f′(x)= 4x³
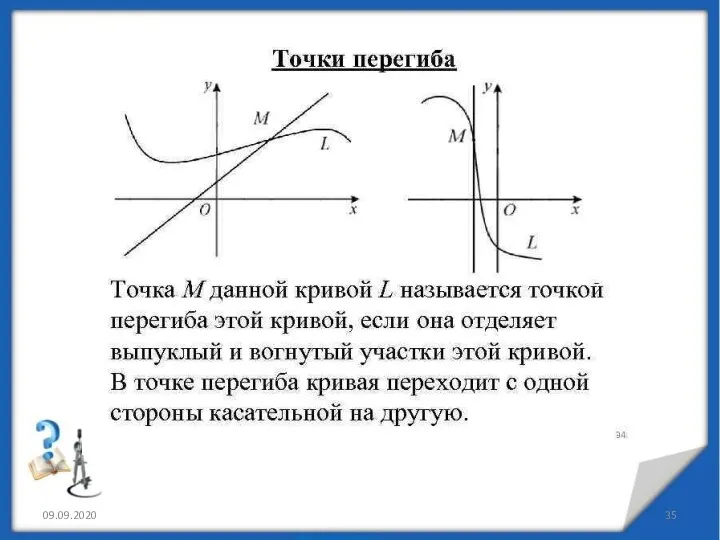
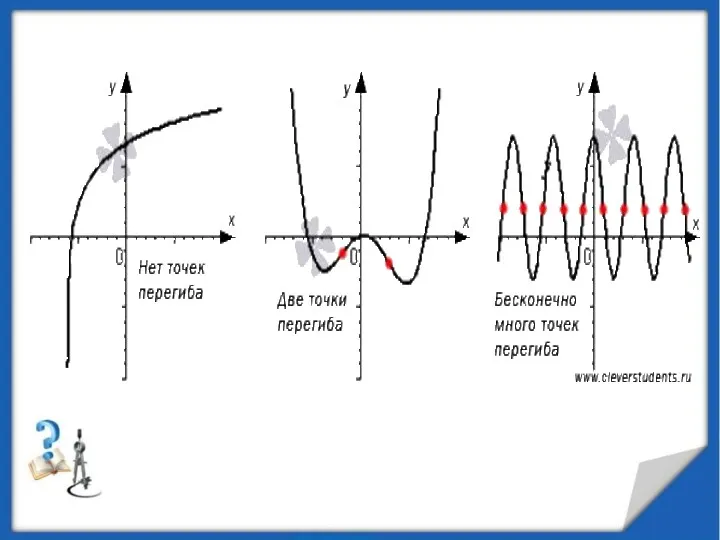
- 34. Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба. Точками перегиба
- 35. 09.09.2020
- 36. 09.09.2020 http://aida.ucoz.ru
- 38. Пример 3. Найти точки перегиба кривых: а) f(x)= 6x² – x³ Находим: f′(x)= 12x – 3x²
- 39. Пример 3. Найти точки перегиба кривых: б) Находим: f′′(x)=0 x=0 – критическая точка, в которой вторая
- 41. Скачать презентацию
























 Вычитание удобным способом
Вычитание удобным способом Признаки деления на 3, на 9
Признаки деления на 3, на 9 Физкультминутка(презентация)
Физкультминутка(презентация) Транспортная задача
Транспортная задача Некоторые свойства прямоугольного треугольника. Урок 47
Некоторые свойства прямоугольного треугольника. Урок 47 Равные треугольники. Высота, биссектриса, медиана. 7 класс
Равные треугольники. Высота, биссектриса, медиана. 7 класс Формулы сокращенного умножения
Формулы сокращенного умножения устный счет
устный счет Сумматор
Сумматор Презентация Ох, уж эта математика
Презентация Ох, уж эта математика Свойства функции. 10 класс
Свойства функции. 10 класс Геометрический смысл производной. Подготовка к ЕГЭ
Геометрический смысл производной. Подготовка к ЕГЭ Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Счастливый случай. Игра
Счастливый случай. Игра Инновационный опыт
Инновационный опыт Задачи на нахождение значений параметра
Задачи на нахождение значений параметра Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива.
Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива. Прямоугольная система координат на плоскости. 6 класс
Прямоугольная система координат на плоскости. 6 класс Ряд натуральных чисел
Ряд натуральных чисел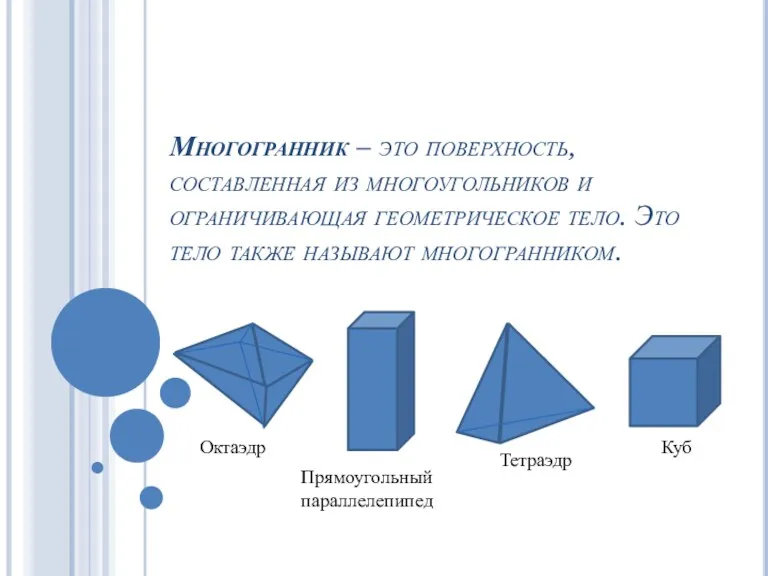 Многогранники и их виды
Многогранники и их виды Понятие движения в геометрии
Понятие движения в геометрии Системы двух уравнений с двумя неизвестными. 7 класс
Системы двух уравнений с двумя неизвестными. 7 класс Треугольники. Виды треугольников. Основные свойства треугольников
Треугольники. Виды треугольников. Основные свойства треугольников Decimals
Decimals Взаимно простые числа. Признак делимости на произведение
Взаимно простые числа. Признак делимости на произведение Сложение и вычитание векторов
Сложение и вычитание векторов устный счёт в виде теста 2 класс Табличное умножение
устный счёт в виде теста 2 класс Табличное умножение Перпендикулярные прямые. Решение задач
Перпендикулярные прямые. Решение задач