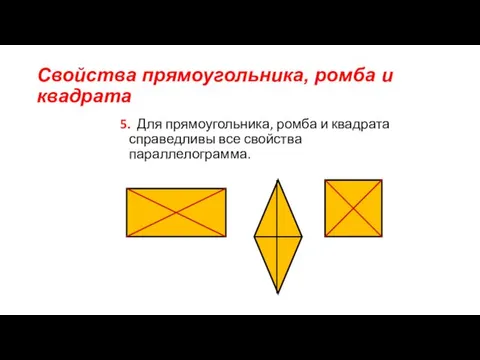
Свойства вписанных и описанных четырёхугольников
1. Четырёхугольник можно вписать в окружность тогда
и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°
А
В
С
D


















 В гости к царице Математике
В гости к царице Математике Методы решения систем линейных уравнений. Графический метод. Метод подстановки. Метод сложения
Методы решения систем линейных уравнений. Графический метод. Метод подстановки. Метод сложения Ковариация, дисперсия и корреляция
Ковариация, дисперсия и корреляция Машина Тьюринга
Машина Тьюринга Понятие функции. 7 класс
Понятие функции. 7 класс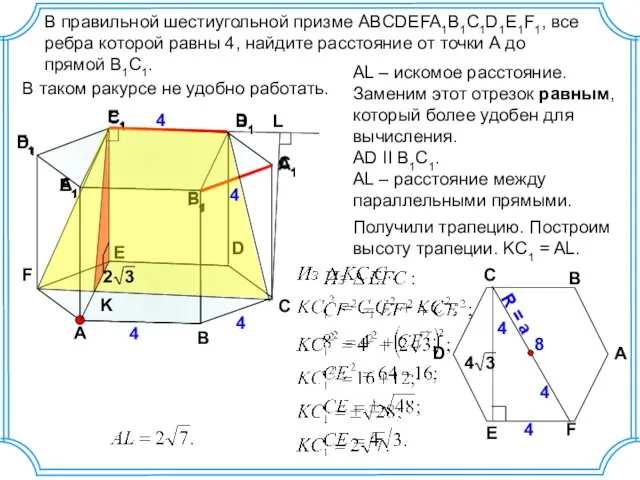 Правильная шестиугольная призма. (№25)
Правильная шестиугольная призма. (№25) Методы решения уравнений
Методы решения уравнений Величина площадь
Величина площадь Правильные многогранники
Правильные многогранники Умножение смешанных дробей
Умножение смешанных дробей Фізичний зміст похідної
Фізичний зміст похідної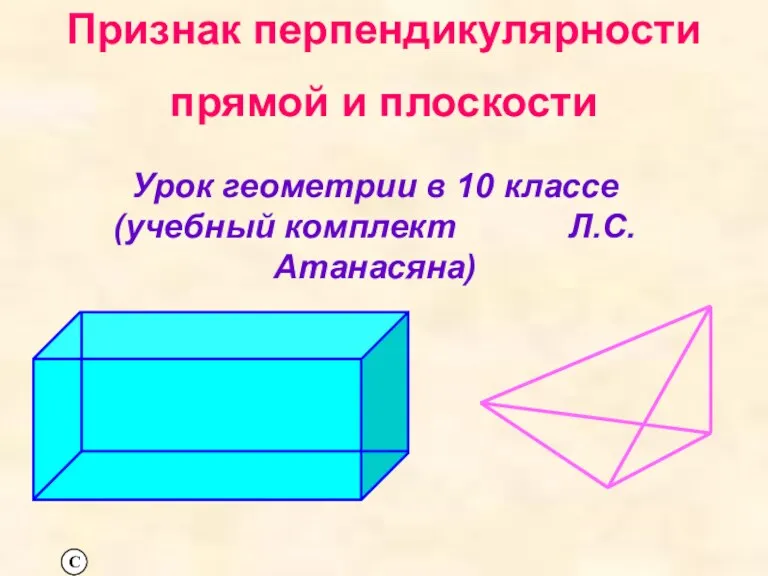 Признак перпендикулярности прямой и плоскости. (10 класс)
Признак перпендикулярности прямой и плоскости. (10 класс) Стандартный вид числа
Стандартный вид числа Двугранный угол. Перпендикулярность плоскостей. Урок 12
Двугранный угол. Перпендикулярность плоскостей. Урок 12 SAS, SPSS, STATISTICA қолданбалы бағдарламалар пакетін қолданып биомедициналық деректерге статистикалық талдаулар жасау
SAS, SPSS, STATISTICA қолданбалы бағдарламалар пакетін қолданып биомедициналық деректерге статистикалық талдаулар жасау Тест по математике Решение логических задач. 5 класс
Тест по математике Решение логических задач. 5 класс Пересечение поверхностей
Пересечение поверхностей Аксонометрия. (Лекция 1)
Аксонометрия. (Лекция 1) Презентация к занятию внеурочной деятельности по математике Как люди научились считать (3 класс)
Презентация к занятию внеурочной деятельности по математике Как люди научились считать (3 класс) Complex numbers
Complex numbers Деление положительных и отрицательных чисел
Деление положительных и отрицательных чисел Теоретические основы математической логики
Теоретические основы математической логики Приемы сравнения чисел
Приемы сравнения чисел Признаки делимости на 2, 5, 10, 4 и 25
Признаки делимости на 2, 5, 10, 4 и 25 Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Parallelogram
Parallelogram Геометричні фігури
Геометричні фігури Необычные геометрические фигуры. 7 класс
Необычные геометрические фигуры. 7 класс