Содержание
- 2. Выборочная и теоретическая ковариации Ковариация является мерой взаимосвязи между двумя переменными Если x и y -
- 3. При наличии n наблюдений двух переменных (x и y) выборочная ковариация между x и y задается
- 4. Можно сказать, что ковариация характеризует сопряженность вариации двух признаков и представляет собой статистическую меру взаимодействия двух
- 5. Если теоретическая ковариация неизвестна, то для ее оценки может быть использована выборочная ковариация, вычисленная по ряду
- 6. Эта оценка будет иметь отрицательное смещение. Причина заключается в том, что выборочные отклонения измеряются по отношению
- 7. Можно рассчитать несмещенную оценку путем умножения выборочной оценки на n / (n - 1) . Если
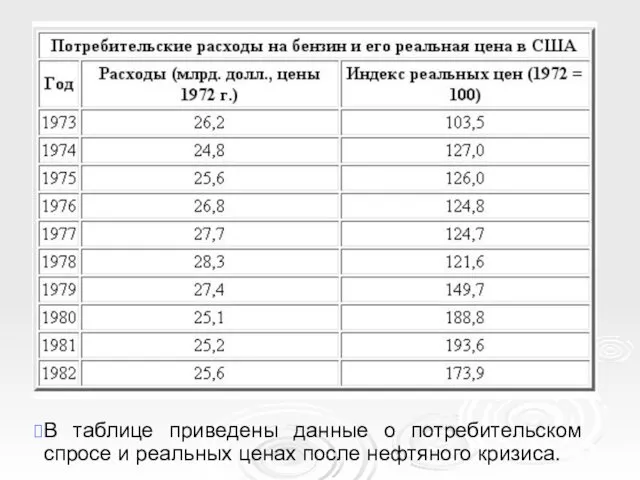
- 8. Пример расчета ковариации Cо времен нефтяного кризиса 1973 г. реальная цена на бензин, т.е. цена бензина,
- 9. В таблице приведены данные о потребительском спросе и реальных ценах после нефтяного кризиса.
- 10. Реальная цена вычислялась путем деления индекса номинальной цены на бензин, на общий индекс потребительских цен и
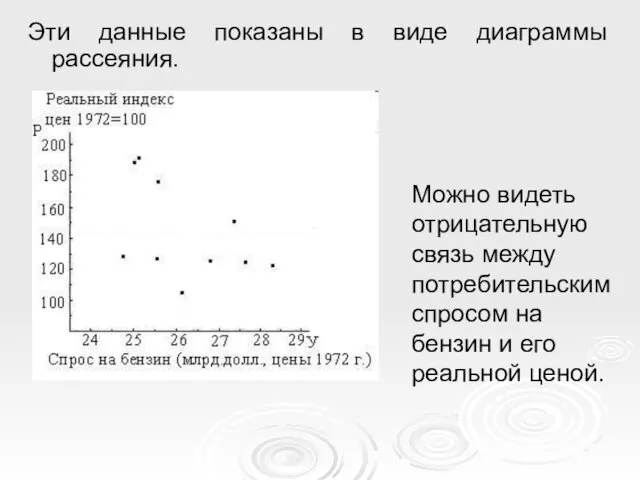
- 11. Эти данные показаны в виде диаграммы рассеяния. Можно видеть отрицательную связь между потребительским спросом на бензин
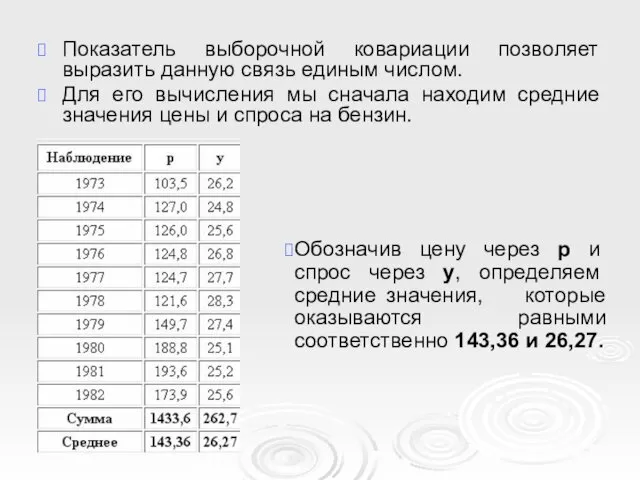
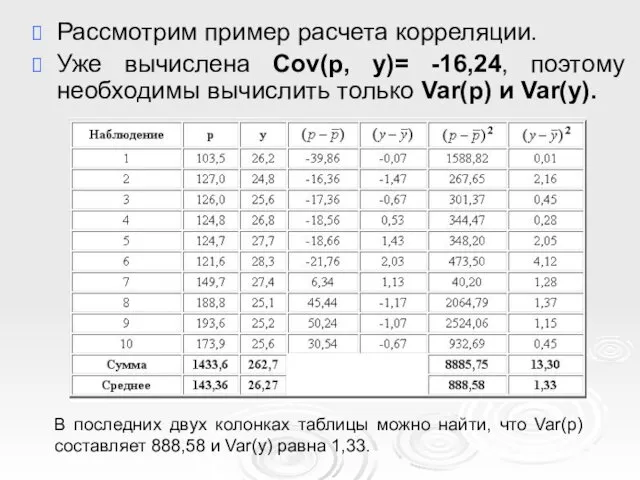
- 12. Показатель выборочной ковариации позволяет выразить данную связь единым числом. Для его вычисления мы сначала находим средние
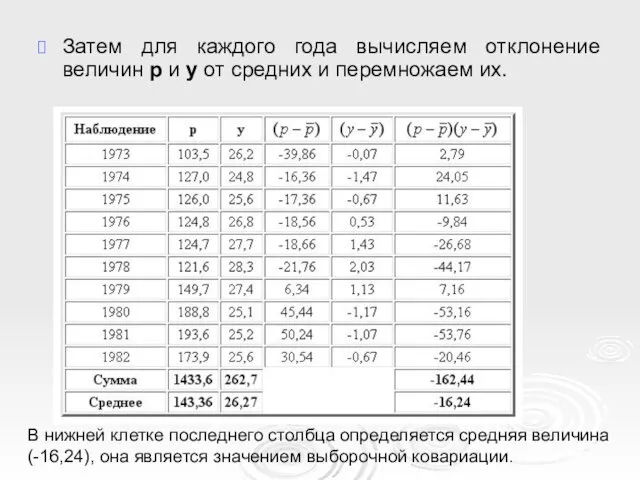
- 13. Затем для каждого года вычисляем отклонение величин p и y от средних и перемножаем их. В
- 14. Ковариация в данном случае отрицательна. Так это и должно быть. Отрицательная связь, как это имеет место
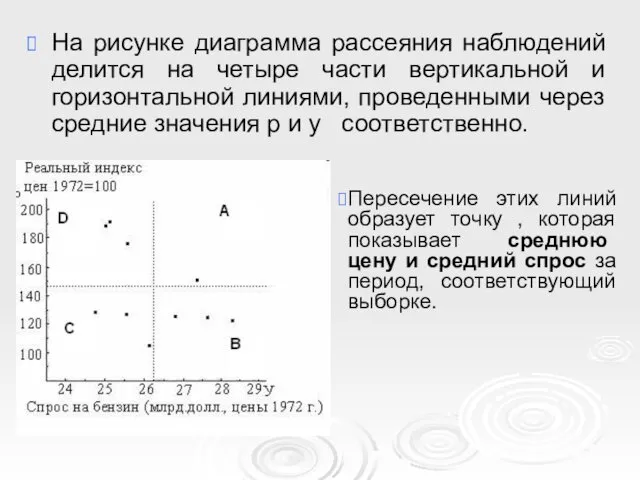
- 15. На рисунке диаграмма рассеяния наблюдений делится на четыре части вертикальной и горизонтальной линиями, проведенными через средние
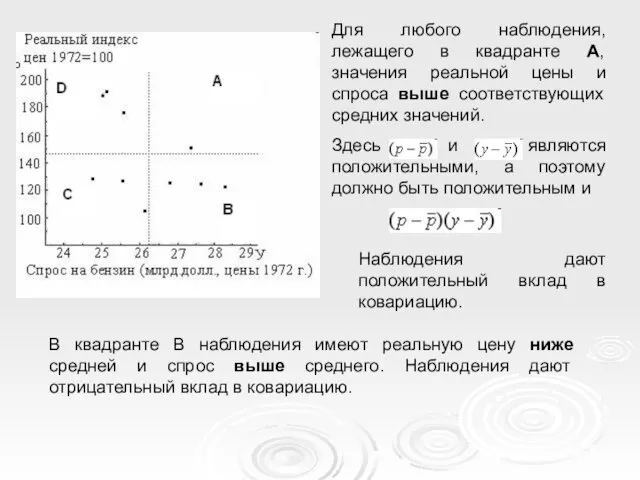
- 16. Для любого наблюдения, лежащего в квадранте А, значения реальной цены и спроса выше соответствующих средних значений.
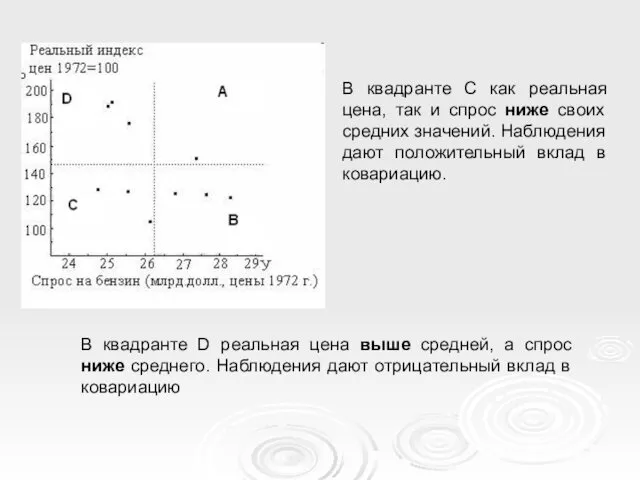
- 17. В квадранте D реальная цена выше средней, а спрос ниже среднего. Наблюдения дают отрицательный вклад в
- 18. Поскольку выборочная ковариация является средней величиной произведения для 10 наблюдений, она будет положительной, если положительные вклады
- 19. Точно так же отрицательные вклады исходят из квадрантов В и D. Поэтому если основное рассеяние идет
- 20. Правила расчета ковариации Существует несколько правил, которые вытекают непосредственно из определения ковариации. Правило 1: Если y
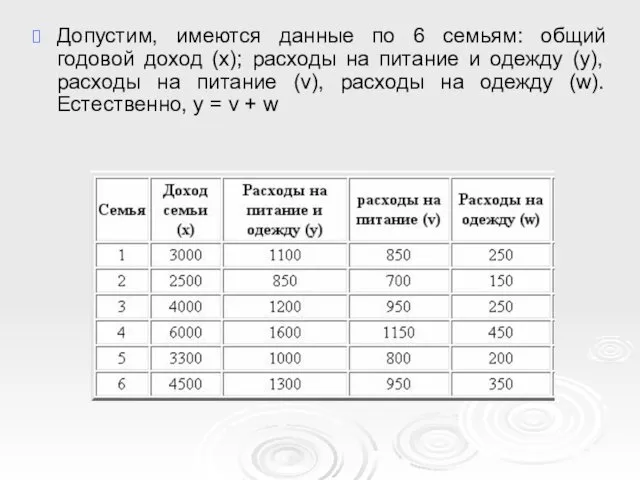
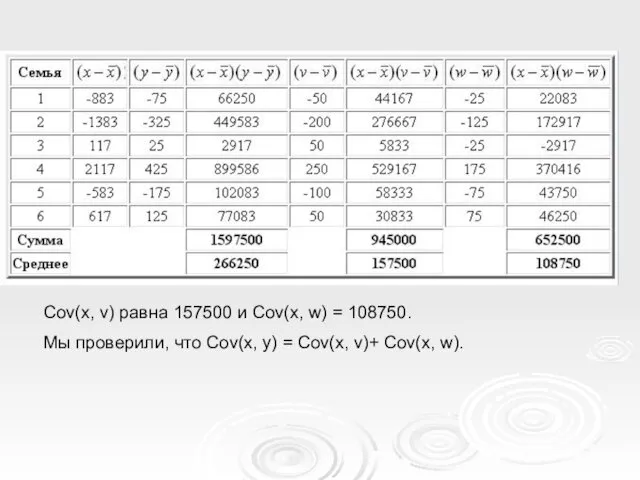
- 21. Допустим, имеются данные по 6 семьям: общий годовой доход (х); расходы на питание и одежду (y),
- 22. Cov(x, v) равна 157500 и Cov(x, w) = 108750. Мы проверили, что Cov(x, y) = Cov(x,
- 23. Именно так и должно быть. Рассмотрим i - ю семью Поскольку yi = vi + wi
- 24. Правило 2: Если y = a z, где a - константа, то Cov(x, y) = a
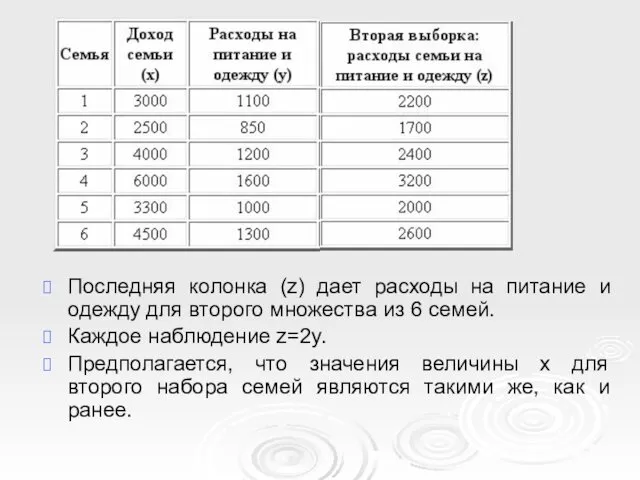
- 25. Последняя колонка (z) дает расходы на питание и одежду для второго множества из 6 семей. Каждое
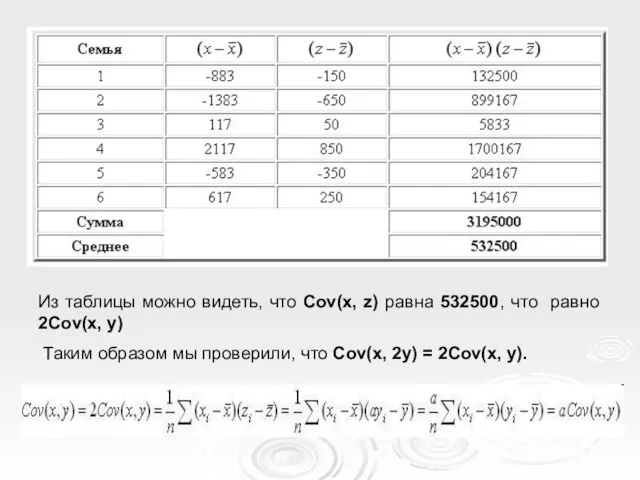
- 26. Из таблицы можно видеть, что Cov(x, z) равна 532500, что равно 2Cov(x, y) Таким образом мы
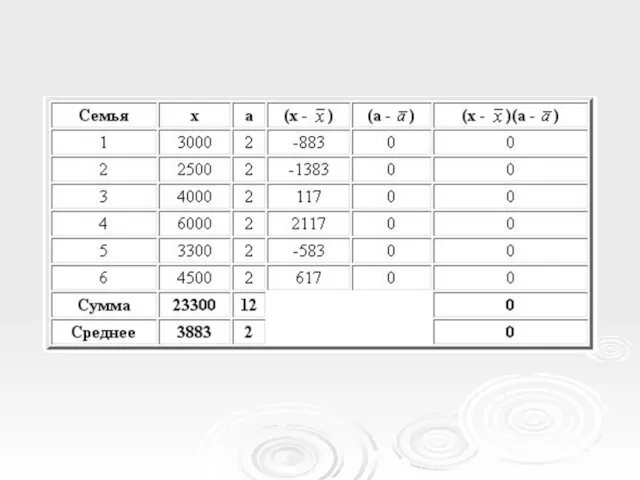
- 27. Правило 3: Если y = a, где a - константа, то Cov(x, y) = 0. Допустим,
- 29. Выборочная дисперсия, правила расчета дисперсии Для выборки из n наблюдений x1, ...,xn выборочная дисперсия определяется как
- 30. Заметим, что дисперсия переменной x может рассматриваться как ковариация между двумя величинами x: Кроме того можно
- 31. Существует несколько правил для расчета дисперсии, которые являются аналогами правил для ковариации. Правило 1: Если y
- 32. Правило 2: Если y = a z, где a - константа, то Var(y) = a2Var(z). Доказательство:
- 33. Правило 3: Если y = a, где a - константа, то Var(y) = 0. По правилу
- 34. Правило 4: Если y = v + a, где a - константа, то Var(y) = Var(v).
- 35. Корреляционная зависимость Функциональная зависимость- связь, при которой каждому значению независимой переменной x значение переменной y Статистическая
- 36. Частным случаем статистической зависимости является корреляционная зависимость. Корреляционная зависимость- связь, при которой каждому значению независимой переменной
- 37. Корреляционная связь является «неполной» зависимостью, которая проявляется не в каждом отдельном случае, а только в средних
- 38. Наиболее разработанной в эконометрике является методология парной линейной регрессии, рассматривающая влияние переменной х на переменную y
- 39. Корреляционный анализ Заключается в количественном определении тесноты связи между двумя признаками (при парной связи) и между
- 40. Коэффициент корреляции Коэффициент корреляции является более точной мерой зависимости между величинами. Подобно дисперсии и ковариации, коэффициент
- 41. Если x и y независимы, то px,y =0, так как равна нулю теоретическая ковариация. Если между
- 42. Качественные характеристики связи
- 43. Выборочный коэффициент корреляции r для переменных x и y определяется путем замены теоретических дисперсий и ковариации
- 44. Выборочный коэффициент корреляции имеет максимальное значение, равное 1, которое получается при строгой линейной положительной зависимости между
- 45. Рассмотрим пример расчета корреляции. Уже вычислена Cov(p, y)= -16,24, поэтому необходимы вычислить только Var(p) и Var(y).
- 47. Из примера видим, что коэффициент корреляции незначительно отличается от нуля. Одна из причин в получении такого
- 48. Еще одна причина - не учтено влияние увеличения дохода на потребительский спрос в целом и на
- 49. Чтобы выделить эти два фактора используют коэффициент частной корреляции: где rxy.z - коэффициент частной корреляции между
- 50. В примере со спросом на бензин можно вычислить корреляцию между ценой и располагаемым личным доходом и
- 51. Результат получился лучше
- 52. Выводы Таким образом, корреляция может быть 3-х видов: Парная – связь между двумя признаками Частная –
- 53. Коэффициенты корреляции как статистические величины подвергаются в анализе оценке на достоверность Для оценки значимости коэффициента корреляции
- 54. Выдвигается гипотеза о равенстве нулю коэффициента корреляции rxy =0. Если гипотеза отвергается, то коэффициент корреляции признается
- 55. Формула расчета критерия Стьюдента
- 57. Скачать презентацию































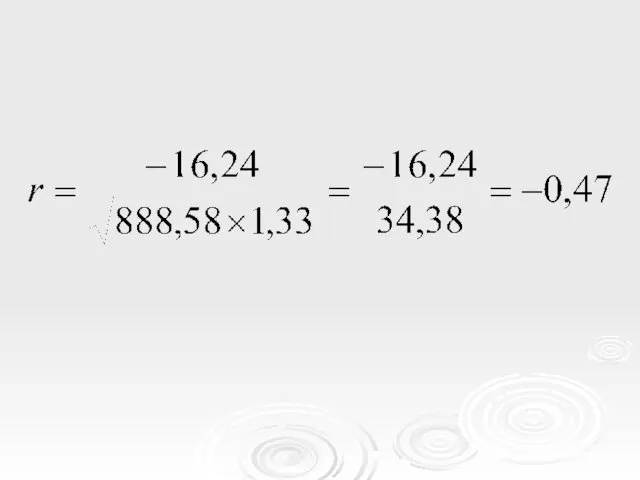









 Пропорциональные отрезки в прямоугольном треугольнике (урок-квест)
Пропорциональные отрезки в прямоугольном треугольнике (урок-квест)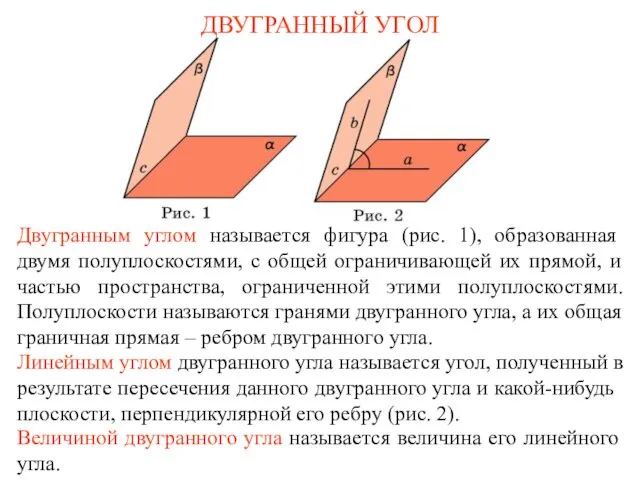 Двугранный угол. Задачи
Двугранный угол. Задачи Начальные геометрические сведения. 7 класс
Начальные геометрические сведения. 7 класс Устный счёт
Устный счёт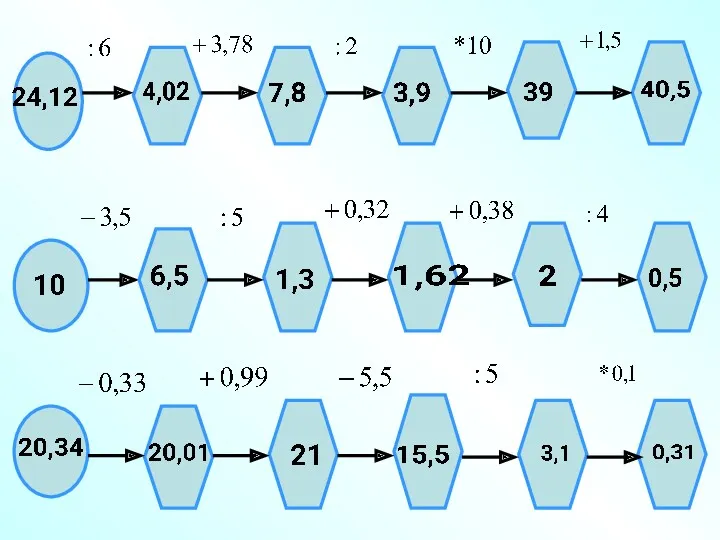 Решение задач на проценты с помощью пропорций
Решение задач на проценты с помощью пропорций Действия с десятичными и обыкновенными дробями
Действия с десятичными и обыкновенными дробями Построение биссектрисы угла
Построение биссектрисы угла Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Площадь и периметр фигуры, составленной из двух-трёх прямоугольников (квадратов). Урок математики для учащихся 4 класса
Площадь и периметр фигуры, составленной из двух-трёх прямоугольников (квадратов). Урок математики для учащихся 4 класса Ключевые символы-как алгоритм при решении задач на уроках математики
Ключевые символы-как алгоритм при решении задач на уроках математики Свойства логарифмов. Логарифмическая функция
Свойства логарифмов. Логарифмическая функция Презентация по геометрии для 10 класса Признак перпендикулярности прямой и плоскости. К учебнику Атанасяна.
Презентация по геометрии для 10 класса Признак перпендикулярности прямой и плоскости. К учебнику Атанасяна. Число і цифра 1. Написання цифри 1
Число і цифра 1. Написання цифри 1 Презентация для детей Название геометрических предметов
Презентация для детей Название геометрических предметов Презентация к уроку математики на тему Правила обозначения геометрических фигур буквами.
Презентация к уроку математики на тему Правила обозначения геометрических фигур буквами. Арифметический квадратный корень. Понятие квадратного корня из неотрицательного числа
Арифметический квадратный корень. Понятие квадратного корня из неотрицательного числа Презентация к фрагменту урока в 1 классе. Тема Числа и цифры 1 и 2
Презентация к фрагменту урока в 1 классе. Тема Числа и цифры 1 и 2 Учимся писать цифры.
Учимся писать цифры. Презентация по математике Составные задачи по программе Перспективная школа автор Чуракова, в 3х классах.
Презентация по математике Составные задачи по программе Перспективная школа автор Чуракова, в 3х классах. Метод змінного середнього. Математичні методи побудови прогнозів
Метод змінного середнього. Математичні методи побудови прогнозів Лічба предметів. Множина
Лічба предметів. Множина Прямоугольный треугольник. Решение задач. 7 класс
Прямоугольный треугольник. Решение задач. 7 класс Многоугольники
Многоугольники Общие сведения о кривых поверхностях
Общие сведения о кривых поверхностях Презентация по математике. Тема Сложение однозначных чисел с переходом через десяток вида ...+8, ....+9
Презентация по математике. Тема Сложение однозначных чисел с переходом через десяток вида ...+8, ....+9 Равнобедренные треугольники. Задачи
Равнобедренные треугольники. Задачи Раскрытие скобок и заключение в скобки
Раскрытие скобок и заключение в скобки Решение задач с помощью уравнений. Устный счет
Решение задач с помощью уравнений. Устный счет