Содержание
- 2. План лекции Комбинаторика как наука Правило сложения Правило умножения Понятие факториала числа Размещения Перестановки Сочетания Алгоритм
- 3. Комбинаторика как наука Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно
- 4. Правило суммы Пусть имеется n попарно непересекающихся множеств содержащих элементов соответственно. Число способов, которыми можно выбрать
- 5. Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в
- 6. Правило произведения В дальнейшем будет часто использоваться Определение: Кортеж - конечная последовательность (допускающая повторения) элементов какого-нибудь
- 7. Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в
- 8. Понятие факториала числа Определение. Факториал – произведение натуральных чисел от единицы до какого-либо данного натурального числа
- 9. Размещения Размещениями из n элементов по m элементов (m
- 10. Размещения без повторений: Пример. В группе 30 студентов. Сколькими способами могут быть выбраны староста и представитель
- 11. Размещения с повторениями. Различные кортежи длины m, составленные из элементов данного множества, содержащего n элементов, так,
- 12. Перестановки Перестановками из n элементов называются размещения из этих n элементов по n элементов. Перестановки –
- 13. Пример. Для дежурства в общежитии в течение учебной недели (5 дней) выделены 5 студентов. Сколькими способами
- 14. Перестановки с повторениями: это кортежи, в которых элемент повторяется раз. Пример. Сколько различных «слов» можно составить,
- 15. Сочетания Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по
- 16. Пример. Для проведения экзамена создается комиссия из двух преподавателей. Сколько различных комиссий можно составить, если есть
- 17. Пример. Возьмем плоды банан, ананас, киви, яблоко и репа . Какие сочетания из этих плодов, взятых
- 19. Алгоритм решения комбинаторных задач При решении комбинаторных задач следует ответить на следующие вопросы: Из какого множества
- 20. Пример. В фортепианном кружке дома детского творчества занимается 10 человек, в кружке художественного слова – 15,
- 21. 2. Проводя подобные рассуждения, выбираем пианистов: 3 из 10 – способов. 3. Певцов: 5 из 12
- 22. Основоположники комбинаторики как раздела математики Пьер де Ферма́ 1601 – 1665 гг. Блез Паскаль 1623 –
- 24. Скачать презентацию





















 Прогулка в Простоквашино
Прогулка в Простоквашино Математика в моей профессии
Математика в моей профессии Ділення десяткових дробів
Ділення десяткових дробів Меры разброса
Меры разброса Стандартный вид числа. Санкт - Петербург в цифрах
Стандартный вид числа. Санкт - Петербург в цифрах 5 санына көбейту және бөлу кестесі
5 санына көбейту және бөлу кестесі Линейная функция
Линейная функция Регрессио́нный анализ. Примеры применения регрессионного анализа
Регрессио́нный анализ. Примеры применения регрессионного анализа Математический калейдоскоп. Софизмы
Математический калейдоскоп. Софизмы Сумма углов в треугольнике
Сумма углов в треугольнике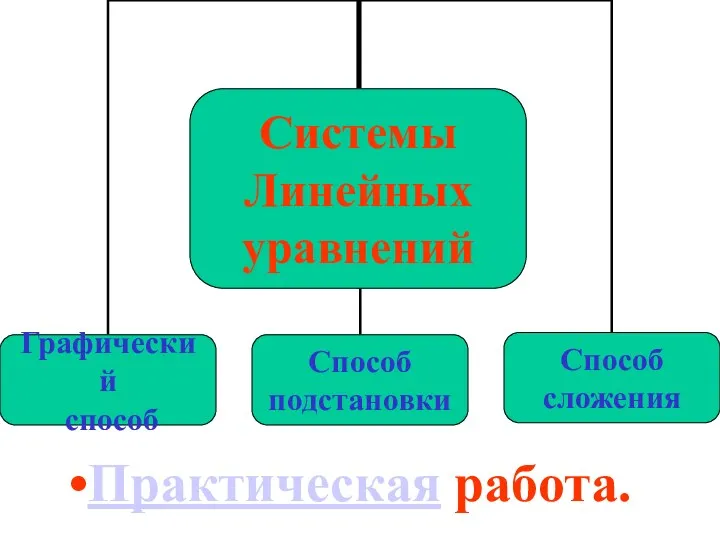 Системы линейных уравнений
Системы линейных уравнений Трапеция
Трапеция Движение по прямой. Задачи
Движение по прямой. Задачи Умножение и деление рациональных чисел
Умножение и деление рациональных чисел Презентация к уроку по математике
Презентация к уроку по математике Решение линейных уравнений (6 класс)
Решение линейных уравнений (6 класс) Дифференциальные уравнения
Дифференциальные уравнения Умножение многочлена на многочлен
Умножение многочлена на многочлен Предел функции
Предел функции Деление и дроби
Деление и дроби Модуль числа. Уравнения и неравенства, содержащие модуль
Модуль числа. Уравнения и неравенства, содержащие модуль Разложение на множители с помощью формул сокращенного умножения. 7 класс
Разложение на множители с помощью формул сокращенного умножения. 7 класс Деление с остатком
Деление с остатком Проектируем сад
Проектируем сад презентация к внеклассному мероприятию Путешествие в страну математика
презентация к внеклассному мероприятию Путешествие в страну математика Презентация к уроку математики по теме: Виды треугольников. 3 класс УМК Школа России
Презентация к уроку математики по теме: Виды треугольников. 3 класс УМК Школа России Интегрированный урок литературы и математики
Интегрированный урок литературы и математики Числовые и алгебраические выражения
Числовые и алгебраические выражения