Компланарные векторы, правило параллелепипеда презентация

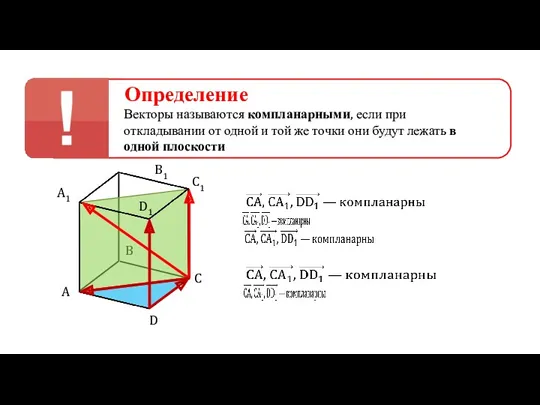
Определение
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости
C
A
B
D
A1
B1
C1
D1

— Любые два вектора компланарны
— Три вектора, среди которых имеются два коллинеарных, также компланарны
— Три произвольных вектора могут быть как компланарными, так и некомпланарными

Признак компланарности трёх векторов
Доказательство:
B1
C
A1
O
A
B
Что и требовалось доказать

Утверждение, обратное признаку компланарности векторов:

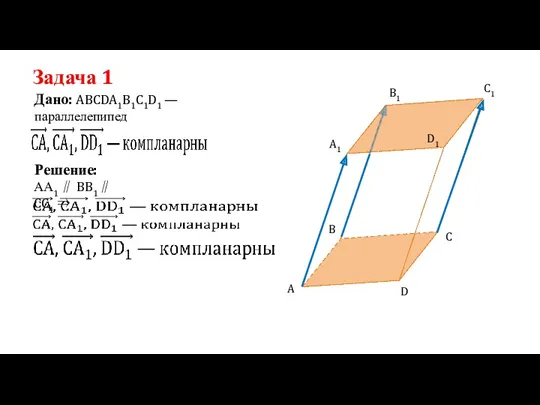
Задача 1
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:
АА1 ∥ BB1∥ CC1 ⇒
A
D
C
B
B1
A1
D1
C1

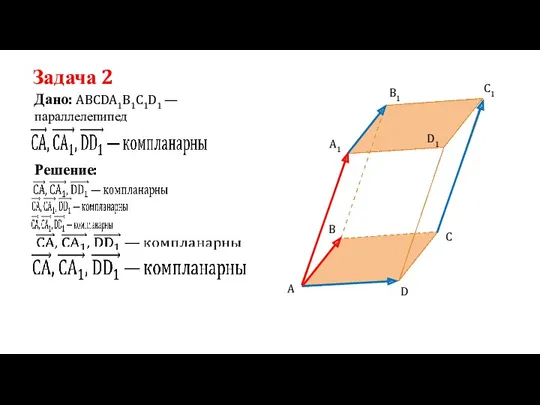
Задача 2
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:
A
D
C
B
B1
A1
D1
C1

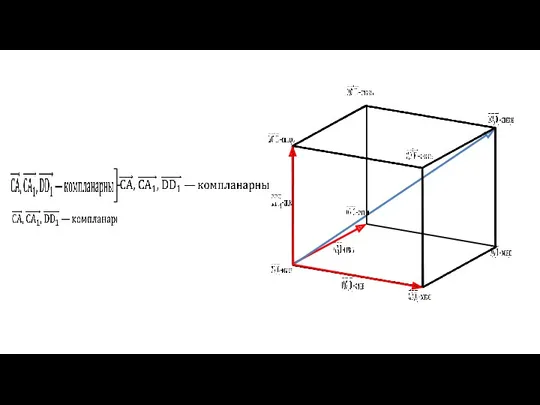
Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.

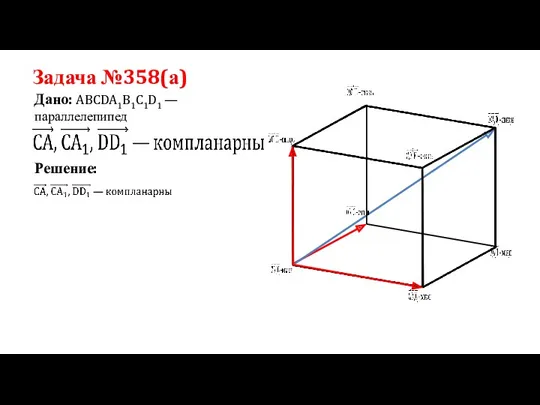
Задача №358(а)
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:

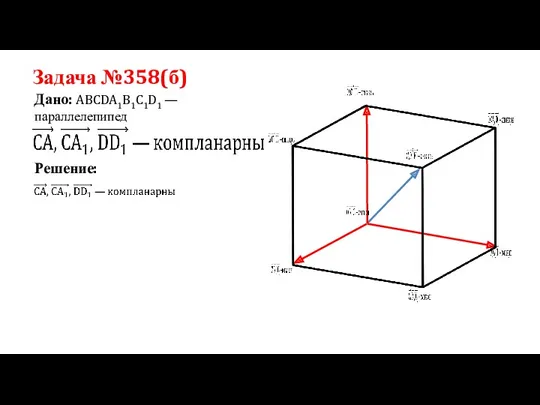
Задача №358(б)
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:

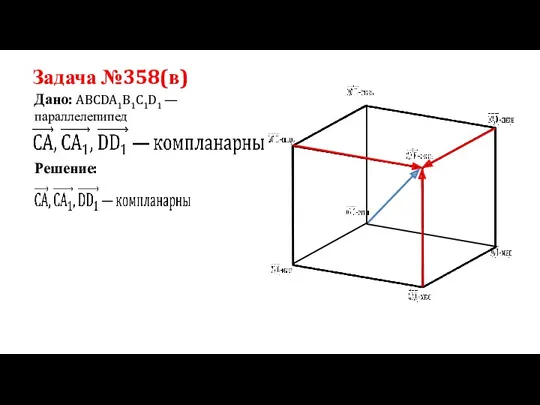
Задача №358(в)
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:

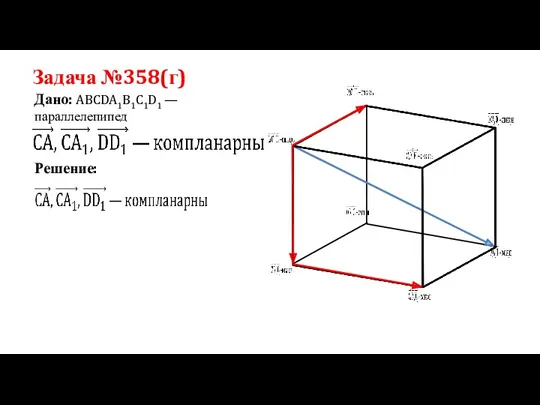
Задача №358(г)
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:

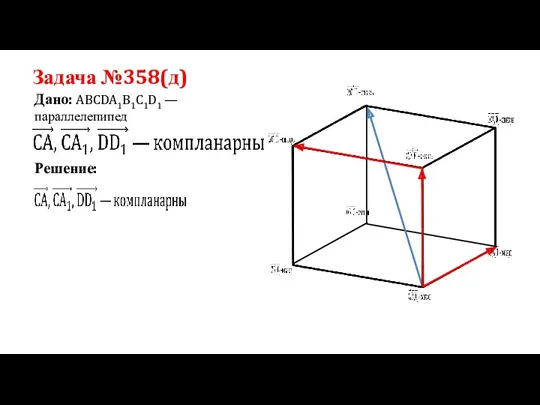
Задача №358(д)
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:

Теорема о разложении вектора по трём некомпланарным векторам
Любой вектор можно разложить по трем данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Теорема о разложении вектора по трём некомпланарным векторам
Любой вектор можно разложить по трем данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Доказательство:

Теорема о разложении вектора по трём некомпланарным векторам
Любой вектор можно разложить по трем данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Доказательство:

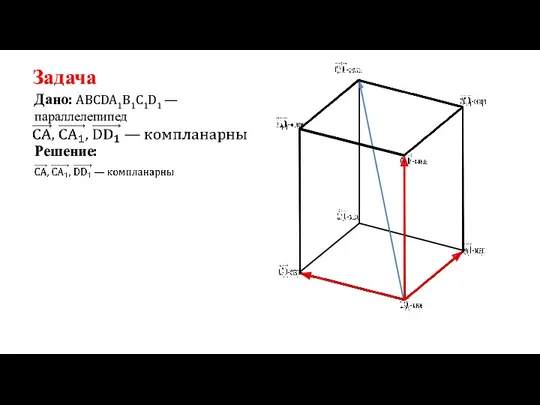
Задача
Дано: ABCDA1B1C1D1 —параллелепипед
Решение: