Впервые мнимые величины появились в работе Дж. Кардано «Великое искусство, или
об алгебраических правилах» в 1545 году.
Пользу мнимых чисел при решении кубических уравнений впервые оценил итальянский ученый Р. Бомбелли (1572).
Символ i предложил российский ученый Л. Эйлер (1777, опубликовано1794).
Задача о выражении степени n из комплексного числа была в основном решена в работах английских ученых А. Муавра (1707, 1724) и Р. Котеса (1722).
Термин «комплексное число» ввел французский ученый Л. Карно (1803).
В употребление термин вошел после работ К. Гаусса (1831).
Полное геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе датского ученого К. Весселя (1799).
Геометрическое представление комплексных чисел называют иногда «диаграммой Аргана» в честь швейцарского ученого Ж. Аргана.
1. Историческая справка







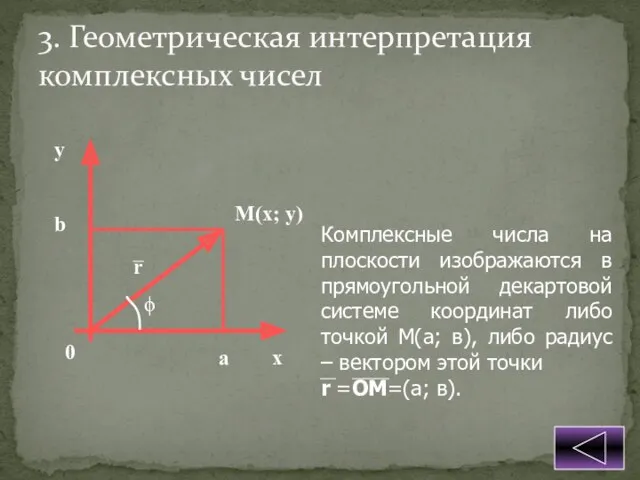




 Свойства сложения
Свойства сложения Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Поставь правильно знаки Игровое упражнение
Поставь правильно знаки Игровое упражнение Закрепление изученного. Решение задач. 4 класс
Закрепление изученного. Решение задач. 4 класс Презентация к уроку математики в 4 классе
Презентация к уроку математики в 4 классе Принципы симметрии
Принципы симметрии Признаки параллельности прямых
Признаки параллельности прямых Устный счёт - гимнастика ума
Устный счёт - гимнастика ума Координатная плоскость
Координатная плоскость производная закрепл
производная закрепл 2 и 3 признаки подобия треугольников
2 и 3 признаки подобия треугольников Презентация Куда приземлится парашютист?(устный счет 1-10)
Презентация Куда приземлится парашютист?(устный счет 1-10) Сложение и вычитание одночленов
Сложение и вычитание одночленов Квадратичная функция, её свойства и график. 8 класс
Квадратичная функция, её свойства и график. 8 класс Что такое функция. Урок алгебры, 7 класс,
Что такое функция. Урок алгебры, 7 класс, Мир многогранников
Мир многогранников Производная сложной функции
Производная сложной функции Интерактивный тренажёр. В гости к Смешарикам Таблица умножения и деления на 6.
Интерактивный тренажёр. В гости к Смешарикам Таблица умножения и деления на 6.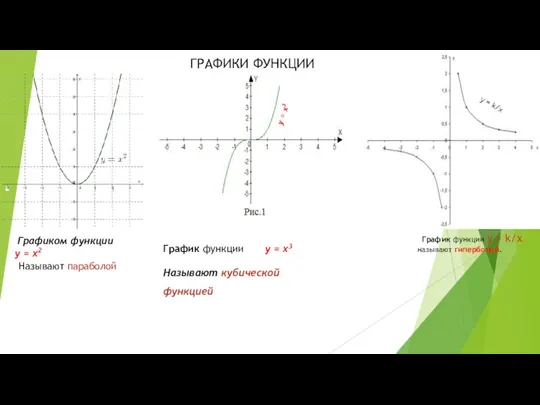 Графики функции. Кубическая парабола
Графики функции. Кубическая парабола Решение задач на готовых чертежах. Вводное повторение. Геометрия. 9 класс
Решение задач на готовых чертежах. Вводное повторение. Геометрия. 9 класс Урок математики в 1 классе Прибавить и вычесть число 3
Урок математики в 1 классе Прибавить и вычесть число 3 Метод интервалов
Метод интервалов Урок - путешествие (презентация) 3 класс, математика, автор М. И. Моро
Урок - путешествие (презентация) 3 класс, математика, автор М. И. Моро Презентация Связь между компонентами и результатом умножения. 2 класс
Презентация Связь между компонентами и результатом умножения. 2 класс Умножение и деление на 7. Седьмая часть числа
Умножение и деление на 7. Седьмая часть числа Теория вероятностей
Теория вероятностей Нахождение числа по его дроби
Нахождение числа по его дроби Свойства корня n-й степени
Свойства корня n-й степени