Содержание
- 2. Лекция 3 2. Операции над комплексными числами. 1. Основные понятия. Комплексные числа
- 5. z=x+iy – это алгебраическая форма записи комплексного числа.
- 6. Операции над комплексными числами . I. Сложение. Рассмотрим комплексные числа в алгебраической форме: II. Умножение.
- 7. Вычислим
- 8. III. Вычитание (обратное сложению). IV. Деление (обратное умножению).
- 9. Чтобы выполнить деление, надо домножить числитель и знаменатель на число, сопряженное знаменателю:
- 10. В результате получим: Пользуясь алгебраической формой комплексного числа, можно производить операции сложения, умножения и вычитания по
- 11. Пример. Выполнить действия I-IV. Решение.
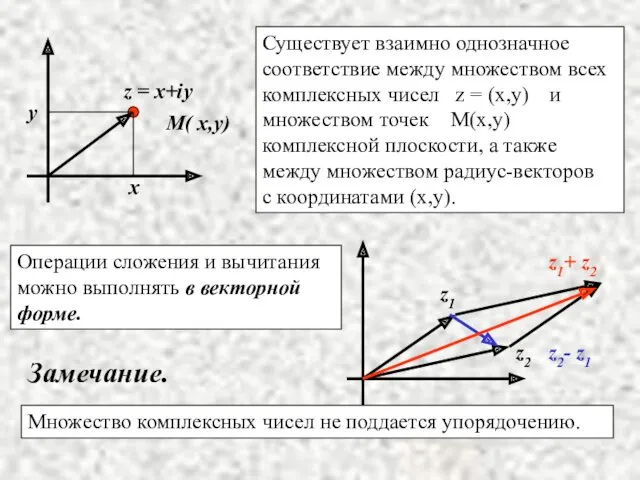
- 12. Изображение комплексных чисел на плоскости. Плоскость, на которой изображаются комплексные числа будем называть комплексной, ось абсцисс
- 13. x y z = x+iy M( x,y) Существует взаимно однозначное соответствие между множеством всех комплексных чисел
- 14. Тригонометрическая и показательная формы записи комплексного числа.
- 15. Таким образом,
- 16. Обозначения. Формула Эйлера Запишем формулы Маклорена для функций
- 17. С учётом:
- 18. Из равенства правых частей следует: формула Эйлера. По формуле Эйлера из (Т) следует (П) показательная форма
- 19. Обозначения.
- 20. Следствия. получим
- 21. Пример. Записать это число в трёх формах, дать геометрическую интерпретацию. Решение.
- 22. Операции над комплексными числами в тригонометрической и показательной формах. Умножение: Рассмотрим
- 23. Деление:
- 24. Возведение в целую степень: Так как формула Муавра.
- 25. Здесь k может принимать все возможные целые значения, но различных (неодинаковых) корней будет только n и
- 27. Замечание. Числа z0, z1,…, zn-1 имеют одинаковый модуль им соответствуют точки на окружности радиуса
- 28. Пример. Обозначим Решение. Различных значений - четыре:
- 30. Скачать презентацию









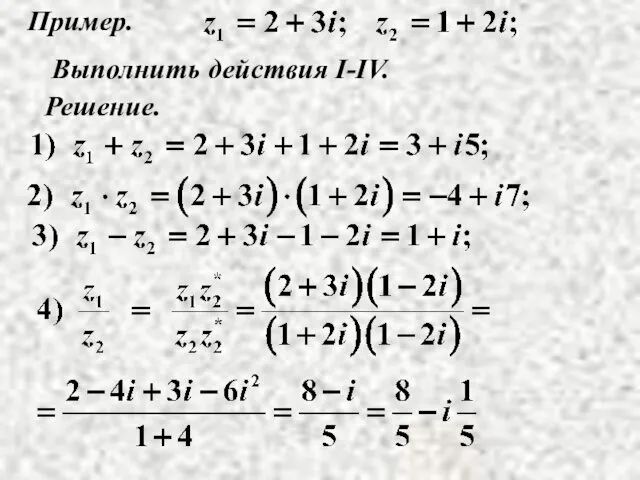







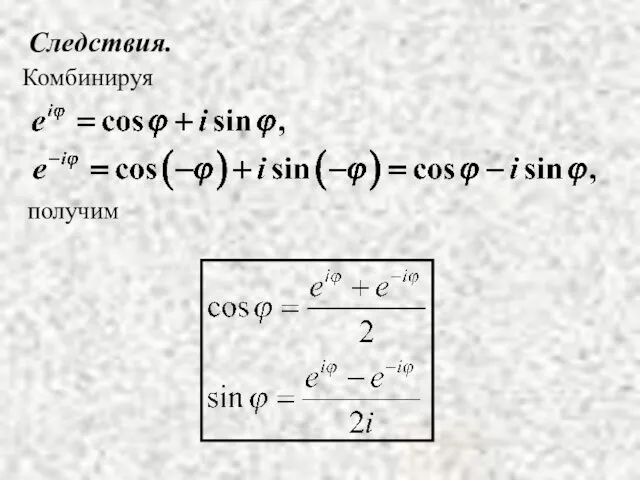





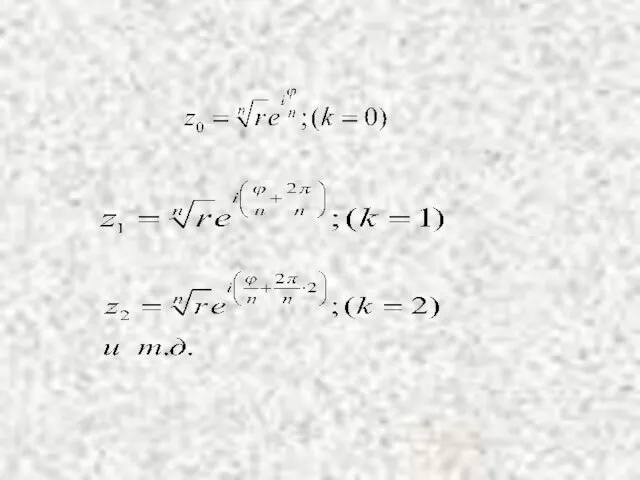


 Экономические задачи в заданиях ЕГЭ по математике
Экономические задачи в заданиях ЕГЭ по математике Состав чисел
Состав чисел Наибольший общий делитель
Наибольший общий делитель Математический тренажер по теме: Сложение и вычитание в пределах 10
Математический тренажер по теме: Сложение и вычитание в пределах 10 Тестовые задания. 7 класс. Геометрия
Тестовые задания. 7 класс. Геометрия Презентация к уроку Задачи на перебор вариантов Диск
Презентация к уроку Задачи на перебор вариантов Диск Разрядные слагаемые числа
Разрядные слагаемые числа Обратная тригонометрическая функция. Устная работа. 10 класс
Обратная тригонометрическая функция. Устная работа. 10 класс Умножение и деление десятичных дробей на натуральные числа
Умножение и деление десятичных дробей на натуральные числа ГЕОМЕТРИЯ 7.02
ГЕОМЕТРИЯ 7.02 Упрощение выражений. Урок 67
Упрощение выражений. Урок 67 В гости к царице Математике
В гости к царице Математике Решение линейных уравнений с одной переменной. 7 класс
Решение линейных уравнений с одной переменной. 7 класс Решение одного тригонометрического уравнения несколькими способами. 10 класс
Решение одного тригонометрического уравнения несколькими способами. 10 класс Свойства сложения. Формула и свойство
Свойства сложения. Формула и свойство Табличное сложение и вычитание
Табличное сложение и вычитание Повторение и закрепление изученного материала по математике (1 класс)
Повторение и закрепление изученного материала по математике (1 класс) Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Сфера и шар
Сфера и шар Скрещивающиеся прямые
Скрещивающиеся прямые Математика. Задания на лето. Часть 5
Математика. Задания на лето. Часть 5 Названия чисел до 20
Названия чисел до 20 Внеклассное мероприятие по математике
Внеклассное мероприятие по математике Теңдеу
Теңдеу Цифры в загадках, пословицах и поговорках
Цифры в загадках, пословицах и поговорках Від’ємні числа, дії над ними
Від’ємні числа, дії над ними Дискретные случайные величины. Тема №4:
Дискретные случайные величины. Тема №4: Презентация по теме Решение неравенства 4 класс по программе Л. Г. Петерсон
Презентация по теме Решение неравенства 4 класс по программе Л. Г. Петерсон