Содержание
- 2. Алгебраическая форма комплексного числа.
- 3. Число, квадрат которого равен –1 называется мнимой единицей и обозначается i или j
- 4. Степени мнимой единицы
- 7. Мнимым числом называется произведение мнимой единицы на действительное число. Примеры: 2j; -5,3j;
- 8. Комплексным числом называется число вида a+bj, где a и b-произвольные действительные числа, j – мнимая единица.
- 9. z=a+bj алгебраическая форма кч
- 10. z=a+bj a=0 Мнимое число z=bj b=0 Действительное число z=a
- 11. Комплексные числа называются равными, если равны их действительные части и коэффициенты мнимых частей. z1=z2 , если
- 12. КЧ равно нулю если равны нулю его действительная часть и коэффициент мнимой части. z=0 , если
- 13. Модулем комплексного числа называется квадратный корень из суммы квадратов его действительной и коэффициента мнимой части.
- 14. Найдите модуль кч: z1=3+4j z2=2-7j z3=3-4j z4=-2-3j
- 15. КЧ называются сопряженными, если они различаются только знаком коэффициента мнимой части. z=a+bj z=a- bj Модули сопряженных
- 16. Являются ли числа сопряженными? 7+3j и -7+3j 2-5j и 2+5j 2,4j+11 и -2,4j+11 8+6j и -8-6j
- 17. Каждому комплексному числу в комплексной плоскости ставится в соответствие одна, и только одна точка; или один,
- 18. yj Ось мнимых чисел x Ось действительных чисел z1=2-3j x=a=2 y=b=-3 2 -3j z1 z2=-4+5j x=-4
- 19. yj Геометрическая сумма комплексных чисел x z1=2-3j 2 -3j z1 z2=4+5j 4 5j z2 z=z1+z2 По
- 20. yj Геометрическая разность комплексных чисел x z1=2-3j 2 -3j z1 z2=4+5j 4 5j z2 z=z1-z2 z3=-z2
- 21. Действия над комплексными числами в алгебраической форме
- 22. Складывать и вычитать КЧ можно только в алгебраической форме. Извлечения корня в алгебраической форме не делают.
- 23. z1=a1+b1 j z2=a2+b2 j 1) Сумма кч z1+z2=(a1+b1j)+(a2+b2j)= a1+b1j+a2+b2j= (a1+a2)+ (b1+b2)j 2) Разность кч z1-z2=(a1+b1j)-(a2+b2j)= a1+b1j
- 24. z1=3+5 j z2=2-6 j 1) Сумма z1+z2=(3+5j)+(2-6j)= 3+5j+2-6j= (3+2)+ (5-6)j= 5 - j 2) Разность z1-z2=(3+5j)-(2-6j)=
- 25. z1=a1+b1 j z2=a2+b2 j 4) Деление кч z1:z2= = -1 a1+b1j a2+b2j Домножаем числитель и знаменатель
- 26. z1=3+5 j z2=2-6 j 4) Деление z1:z2= = -1 3+5j 2-6j Домножаем числитель и знаменатель на
- 27. 5) 6) ·(-j) 7) z1=3 z2=5j z1+z2= ? 3+5j z1=6 z2=-2j z1+z2= ? 6-2j
- 28. Свойства сопряженных чисел. Сумма двух сопряженных чисел есть число, равное 2а. Разность двух сопряженных чисел есть
- 29. yj Геометрическое умножение на ± j и на -1 x z z·j z·(-j) z·(-1)
- 31. Скачать презентацию



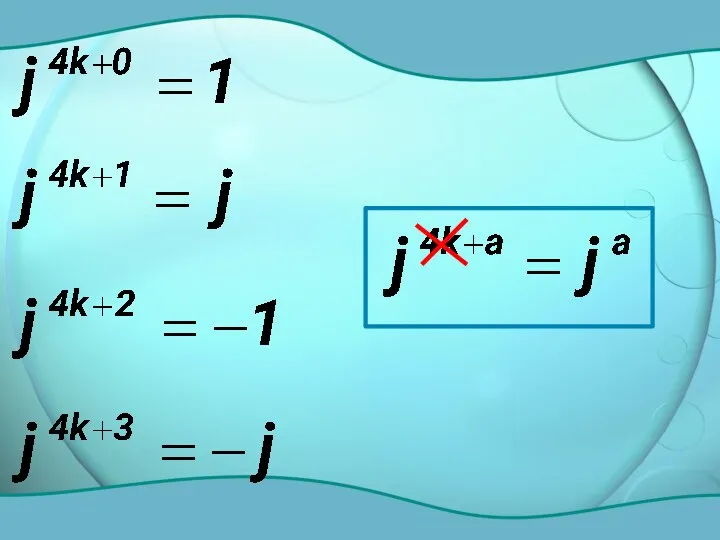
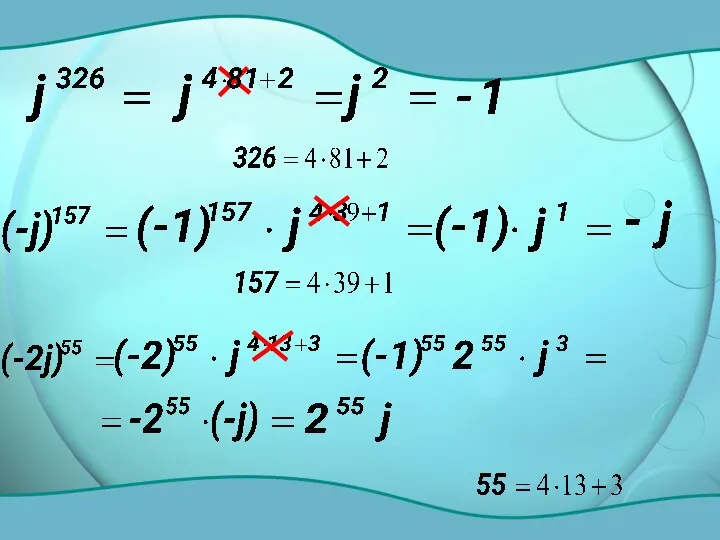



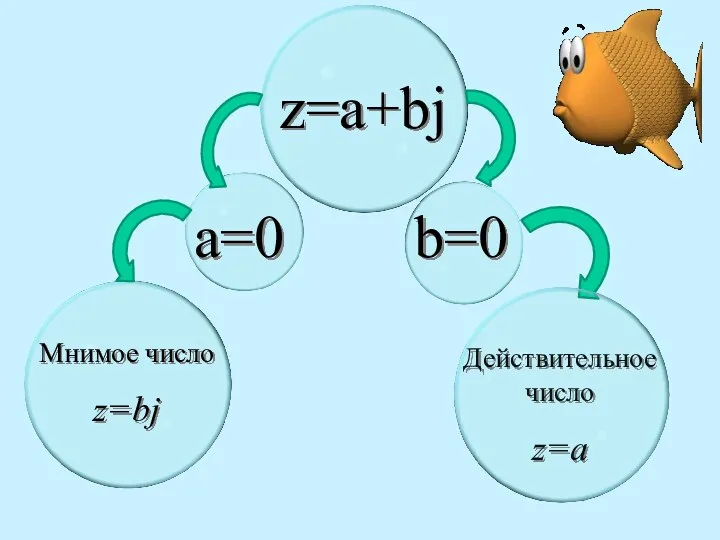







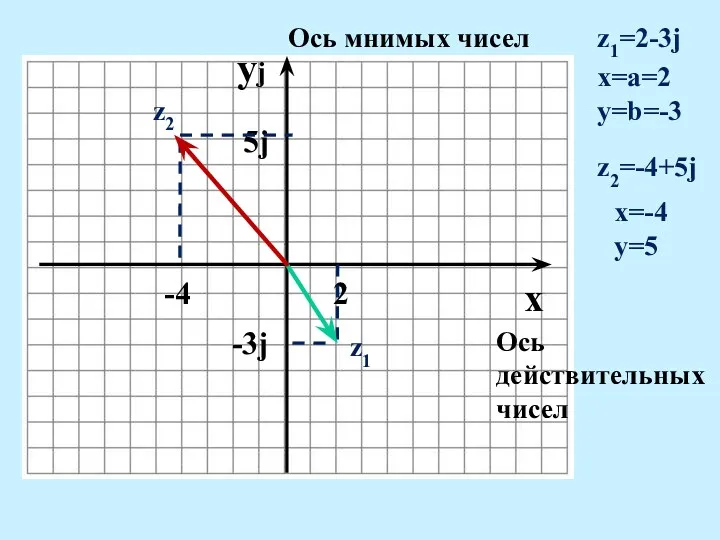
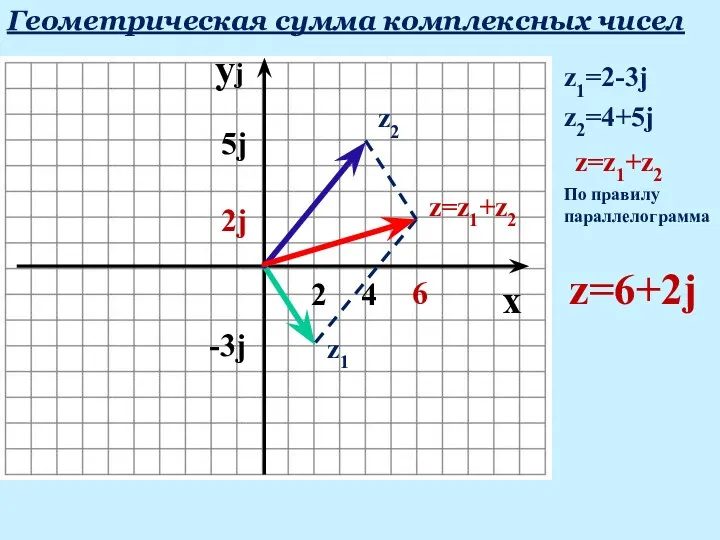
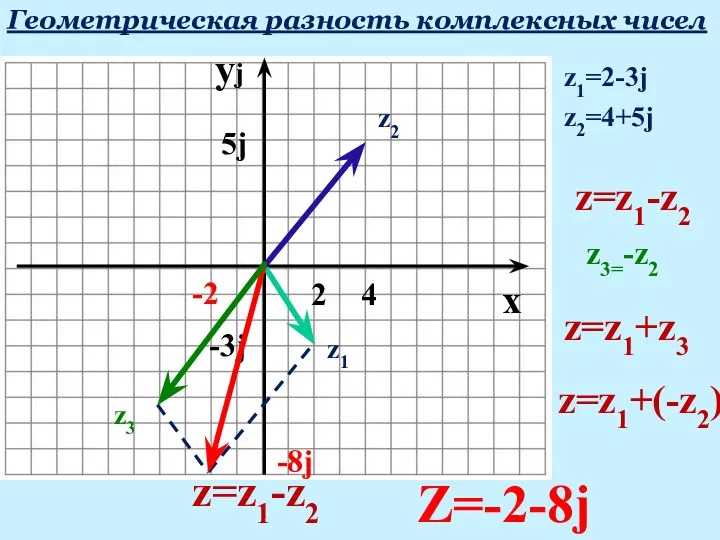






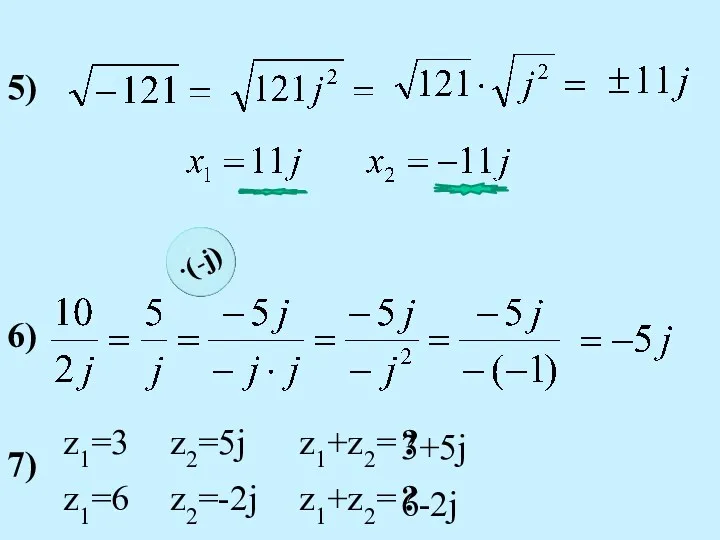

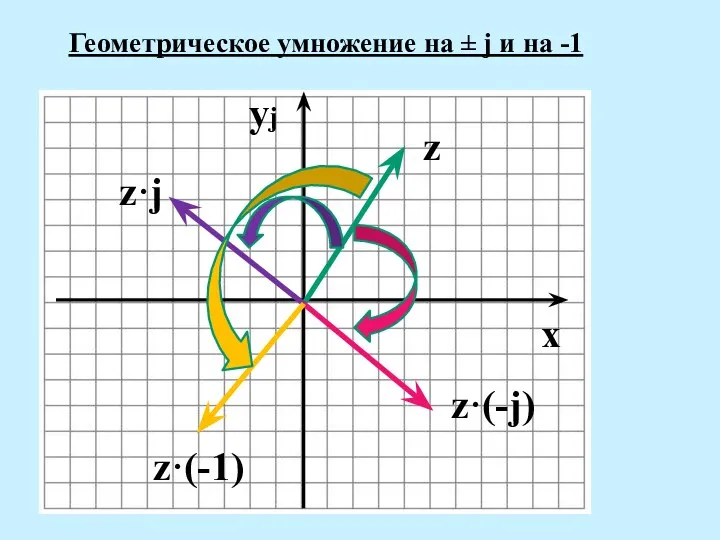
 Таблица умножения в стихах
Таблица умножения в стихах Решение уравнений
Решение уравнений Презентация Симметрия
Презентация Симметрия Теория множеств. Решение задач. Декартово произведение. (Лекция 6)
Теория множеств. Решение задач. Декартово произведение. (Лекция 6) Урок математики в 4 классе УМК Школа 2100
Урок математики в 4 классе УМК Школа 2100 Геометрические фигуры
Геометрические фигуры Степень с натуральным показателем
Степень с натуральным показателем Решение задач на проценты. 5 класс. Урок № 5
Решение задач на проценты. 5 класс. Урок № 5 Все вокруг геометрия
Все вокруг геометрия Evolutionary games. (Lecture 7)
Evolutionary games. (Lecture 7) Многочлены. Действия с многочленами
Многочлены. Действия с многочленами Сложение чисел. Сложение вида +8, +9
Сложение чисел. Сложение вида +8, +9 Открытый урок по математике в четвертом классе по системе Л.В. Занкова
Открытый урок по математике в четвертом классе по системе Л.В. Занкова Устный счет
Устный счет Графический способ решения систем уравнений
Графический способ решения систем уравнений Задачи на проценты. 5 класс
Задачи на проценты. 5 класс Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел
Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел презентация к уроку математики Цифра 1 и чичла 1, 2, 3, 4, 5,
презентация к уроку математики Цифра 1 и чичла 1, 2, 3, 4, 5, Векторная алгебра. Первая лекция
Векторная алгебра. Первая лекция Площадь трапеции
Площадь трапеции Методы статистического вывода: проверка гипотез
Методы статистического вывода: проверка гипотез Синус и косинус
Синус и косинус Презентация Устный счёт 3 класс
Презентация Устный счёт 3 класс Арифметикалық прогрессияның алғашқы nмүшесінің қосындысы
Арифметикалық прогрессияның алғашқы nмүшесінің қосындысы Электронное интерактивное дидактическое мультимедийное пособие Занимательная геометрия
Электронное интерактивное дидактическое мультимедийное пособие Занимательная геометрия Что такое комбинаторика?
Что такое комбинаторика?