Содержание
- 2. 1. Вычисление множеств Дано U={1;2;3;4;5;6;7;8;9;10;11}, A={1;2;3;7;9}, B={3;4;5;6;10;11}, C={2;3;4;7;8}, D={1;7;11}. Вычислить множества 1) 2) 3) 4) 5)
- 3. 2. Выражение множеств Пусть U={1, 2, 3, 4, 5, 6, 7, 8,9}, A={1, 2, 3, 5},
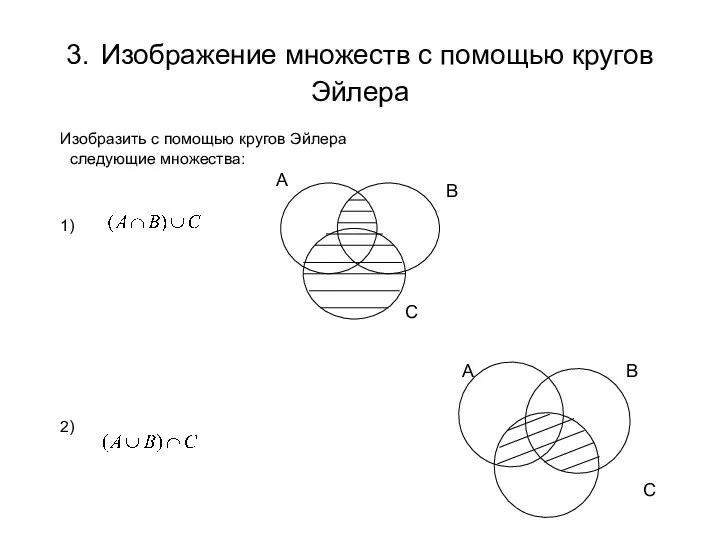
- 4. 3. Изображение множеств с помощью кругов Эйлера Изобразить с помощью кругов Эйлера следующие множества: 1) 2)
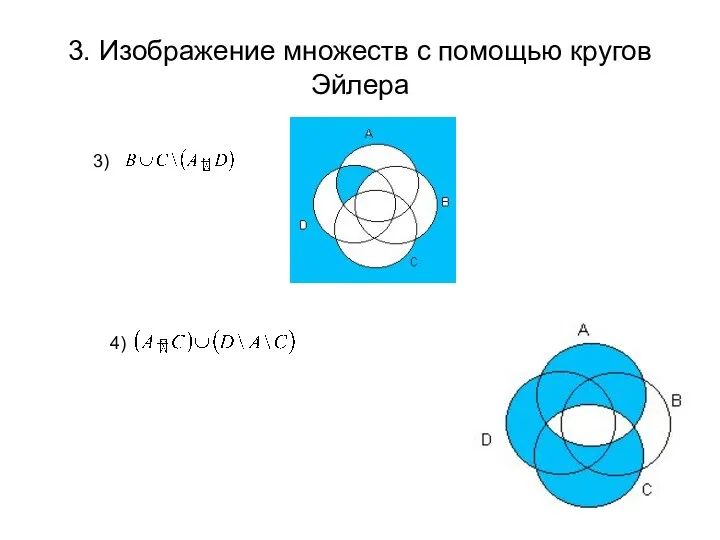
- 5. 3. Изображение множеств с помощью кругов Эйлера 3) 4)
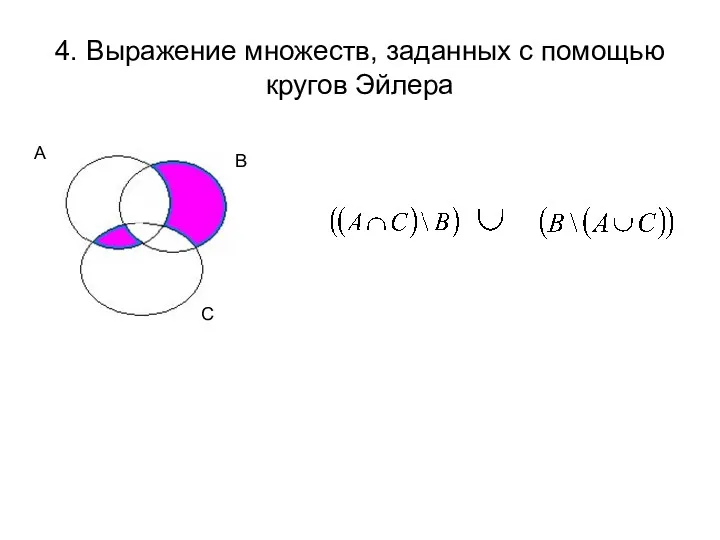
- 6. 4. Выражение множеств, заданных с помощью кругов Эйлера
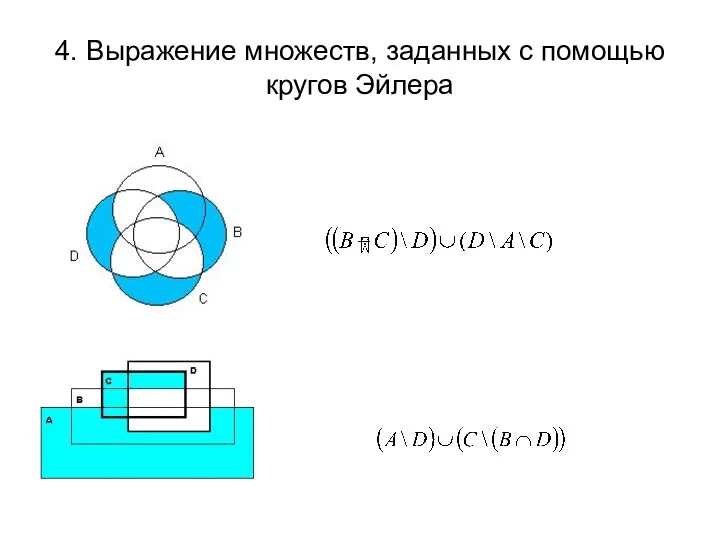
- 7. 4. Выражение множеств, заданных с помощью кругов Эйлера
- 8. Декартово произведение
- 9. Декартово произведение Под упорядоченной парой (а; b) мы будем понимать двухэлементное множество, состоящее из элементов а
- 10. Декартово произведение Определение 2 а) Множество называется декартовым (прямым) произведением n множеств; б) - (n cомножителей)
- 11. Декартово произведение Задача Изобразить множество Пример Очевидно, что , где R- множество действительных чисел, описывает множество
- 12. Декартово произведение Теорема 1 Пусть А, В, С – произвольные множества, тогда
- 13. Доказательство Декартово произведение Следовательно
- 14. Декартово произведение Доказательство Следовательно
- 15. Декартово произведение Доказательство Следовательно
- 17. Скачать презентацию










 Повторение. 8 класс
Повторение. 8 класс Математические модели теории надежности
Математические модели теории надежности Презентация. Ось симметрии. 1 класс
Презентация. Ось симметрии. 1 класс Умножение разности двух выражений на их сумму
Умножение разности двух выражений на их сумму Умножение и деление десятичных дробей. Контрольная работа
Умножение и деление десятичных дробей. Контрольная работа Презентация к НОД
Презентация к НОД Описательная статистика. Урок повторения и закрепления знаний
Описательная статистика. Урок повторения и закрепления знаний Масса неоднородного тела. Тройной интеграл. (Лекция 2-3)
Масса неоднородного тела. Тройной интеграл. (Лекция 2-3) Планиметрия. Треугольники. Равнобедренный треугольник
Планиметрия. Треугольники. Равнобедренный треугольник Площади фигур. Решение задач
Площади фигур. Решение задач Кызыклы математика
Кызыклы математика Частота и вероятность случайного события
Частота и вероятность случайного события Конкурс Тайны математики
Конкурс Тайны математики Правильний опуклий многогранник ікосаедр
Правильний опуклий многогранник ікосаедр Radix sort
Radix sort Использование игр-головоломок для развития самостоятельности в выборе способов решения в старшем дошкольном возрасте
Использование игр-головоломок для развития самостоятельности в выборе способов решения в старшем дошкольном возрасте Аксиомы стереометрии 10 класс
Аксиомы стереометрии 10 класс Уравнения. Путешествие по Солнечной системе
Уравнения. Путешествие по Солнечной системе Геометрическая прогрессия
Геометрическая прогрессия Урок-соревнование для пятиклассников. Натуральные числа
Урок-соревнование для пятиклассников. Натуральные числа Теорема Виета. Квадратное уравнение
Теорема Виета. Квадратное уравнение Засели жильцов 6-7 лет
Засели жильцов 6-7 лет Первые уроки математики в 5 классе. Урок №3
Первые уроки математики в 5 классе. Урок №3 Корiнь n - го степеня
Корiнь n - го степеня Элементы теории игр
Элементы теории игр Прямоугольный треугольник. Стороны прямоугольного треугольника
Прямоугольный треугольник. Стороны прямоугольного треугольника Развитие познавательной активности младших школьников на уроках математики.
Развитие познавательной активности младших школьников на уроках математики. Веселая таблица. Тренажёр таблицы умножения и деления
Веселая таблица. Тренажёр таблицы умножения и деления