Содержание
- 2. Рассмотрим вопрос о нахождении расстояния между точками, если известны их координаты. Пусть на плоскости выбрана прямоугольная
- 3. Докажем формулу для случая, когда и , т. е. когда отрезок AB не параллелен ни одной
- 4. Заметим, что формула верна и для случаев: а) х1 = х2, y1 y2 (отрезок параллелен оси
- 5. Рассмотрим пример. Пусть необходимо вычислить площадь квадрата ABCD, две вершины которого имеют координаты A (8; 8)
- 6. Координаты середины отрезка Рассмотрим вопрос о вычислении координат середины отрезка, если известны координаты концов этого отрезка.
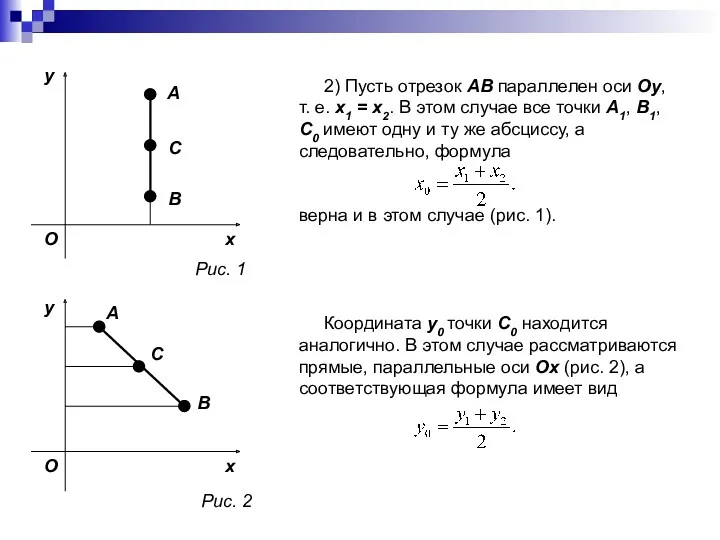
- 7. 2) Пусть отрезок AB параллелен оси Oy, т. е. x1 = x2. В этом случае все
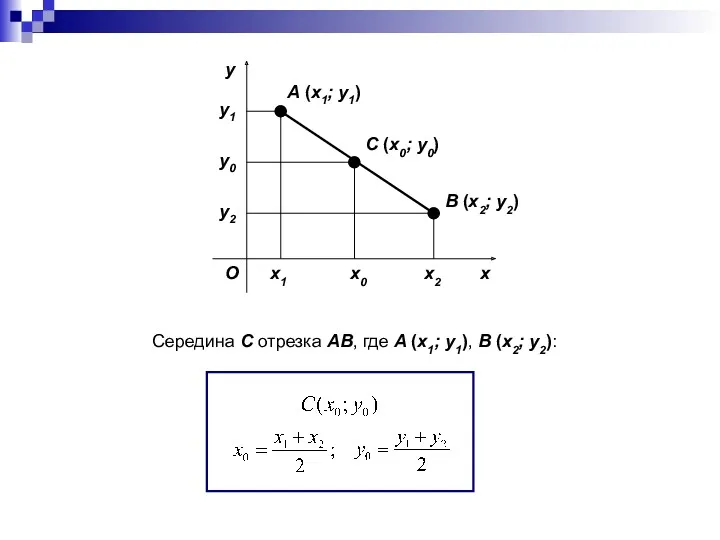
- 8. x y O A (x1; y1) B (x2; y2) C (x0; y0) x1 x2 y1 y2
- 9. Задача. Концами отрезка служат точки A (–8; –5), B (10; 4). Найдите координаты точек C и
- 10. 2) Найдем ординаты точек С и D. Для нахождения ординат точек С и D воспользуемся равенствами
- 12. Скачать презентацию







 Устная нумерация чисел в пределах 100
Устная нумерация чисел в пределах 100 Меры объёма. Литр
Меры объёма. Литр Треугольник Рело, как один из представителей семейства фигур постоянной ширины
Треугольник Рело, как один из представителей семейства фигур постоянной ширины Статистические гипотезы и достоверность статистических характеристик
Статистические гипотезы и достоверность статистических характеристик Арифметическая прогрессия
Арифметическая прогрессия Задачи по теории вероятностей
Задачи по теории вероятностей Поверхностные интегралы 1 и 2 рода, их свойства и вычисление. Лекция 29
Поверхностные интегралы 1 и 2 рода, их свойства и вычисление. Лекция 29 Көлемнің өлшем бірлігі. Текше және оның көлемі
Көлемнің өлшем бірлігі. Текше және оның көлемі Геометричні фігури. Коло. Круг
Геометричні фігури. Коло. Круг Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке ПФЭ (Полный факторный эксперимент)
ПФЭ (Полный факторный эксперимент) Умножение отрицательных чисел
Умножение отрицательных чисел Симметрия относительно плоскости
Симметрия относительно плоскости Теория вероятностей. Способность предвидеть возможные варианты будущего
Теория вероятностей. Способность предвидеть возможные варианты будущего График и свойства степенной функции
График и свойства степенной функции Параллельность прямых и плоскостей. Задания для устного счета. Упражнение 2
Параллельность прямых и плоскостей. Задания для устного счета. Упражнение 2 Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Элементы общей теории ошибок в приложении к обработке результатов измерений
Элементы общей теории ошибок в приложении к обработке результатов измерений Конспект урокаНумерация чисел от 1 до 20 1 класс Школа России
Конспект урокаНумерация чисел от 1 до 20 1 класс Школа России Rezolvarea numerică a sistemelor supradeterminate de ecuaţii algebrice liniare în sensul celor mai mici pătrate
Rezolvarea numerică a sistemelor supradeterminate de ecuaţii algebrice liniare în sensul celor mai mici pătrate Скрещивающиеся прямые. Угол между прямыми
Скрещивающиеся прямые. Угол между прямыми Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Интегрированный урок: математика + биология. Простые и сложные листья
Интегрированный урок: математика + биология. Простые и сложные листья задачи на движение презентация
задачи на движение презентация Математика, русский язык
Математика, русский язык Многогранники. Понятие многогранника. Призма
Многогранники. Понятие многогранника. Призма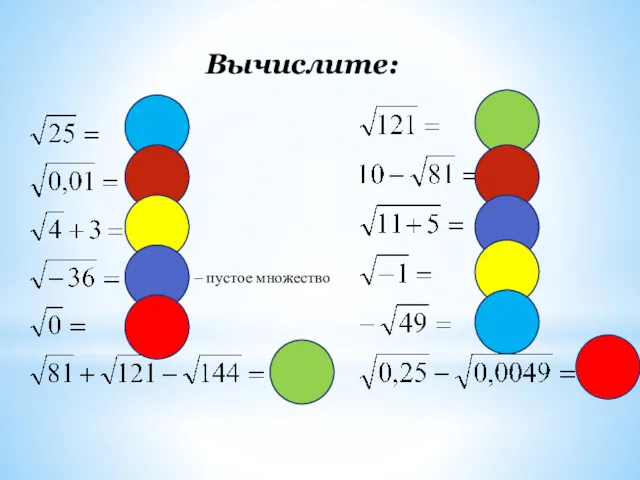 Свойства арифметического квадратного корня
Свойства арифметического квадратного корня