Rezolvarea numerică a sistemelor supradeterminate de ecuaţii algebrice liniare în sensul celor mai mici pătrate презентация
Содержание
- 2. Propoziţie: Pentru orice matrice , următoarele afirmaţii sunt echivalente: ❶ A este o matrice monică; ❷
- 3. ⮞ Condiţii de minim: - diferenţiabilă ⮞ Problema de calcul devine: x* - pseudosoluţie în sensul
- 4. 3.2 Triangularizarea ortogonală a matricelor 3.2.1 Matrici ortogonale Definiţie: Fie o matrice . Matricea Q se
- 5. ⮞ matricele Householder: - vector Houseolder proprietate: 3.2.2 Procedura de triangularizare ortogonală a unei matrici de
- 6. Demonstraţia este constructivă şi constituie însuşi algoritmul de triangularizare ortogonală a matricei A (factorizare QR a
- 7. ⮞ Daca ⇒ ⇒ ⇒ nu există ⮞ Fie ⇒ ⇓ ⮞ Daca ⇒ METODE NUMERICE
- 8. ⮞ Tabloul general al transformărilor: ⇒ ⇒ 3.3 Rezolvarea sistemelor supradeterminate U⋅ ⇒ ⇓ METODE NUMERICE
- 9. 4.1 Formularea problemei - Se consideră o matrice reală, pătratică, de ordin n: Definiţie: Oricare ar
- 10. Teoremă de existenţă: Orice matrice pătratică reală, de ordin n, are exact n valori proprii, în
- 11. 4.2 Forma canonică Schur Definiţie: Două matrici, , se numesc ortogonal asemenea, dacă există o matrice
- 12. Observaţii: ❶ coloanele matricii , ? vectori Schur ai matricii A ❷ Demonstraţia teoremei este constructivă
- 13. ⮞ sedefineşte şirul de matrici - ortogonală; - superior triunghiulară - deplasare (cu rol de accelerare
- 14. ⮞ Faza 1 - procedură directă de aducere a matricei A la forma superior Hessenberg (H)
- 16. Скачать презентацию













 Древний Вавилон
Древний Вавилон Миф. Интеллектуальная игра
Миф. Интеллектуальная игра Угол. Измерение углов. Урок математики в 5 классе
Угол. Измерение углов. Урок математики в 5 классе Процесс решения задачи. 6 класс
Процесс решения задачи. 6 класс Счёт предметов Презентация к уроку математики 1 класс
Счёт предметов Презентация к уроку математики 1 класс Отрезок. Треугольник. Многоугольники
Отрезок. Треугольник. Многоугольники Числа. Геометрические символы
Числа. Геометрические символы Построение сечений многогранников
Построение сечений многогранников Интегрирование рациональных функций
Интегрирование рациональных функций Формулы приведения
Формулы приведения Презентация3
Презентация3 Геометрические тела и их изображение
Геометрические тела и их изображение Наглядность для 1-2 классов по математике Числовы домики (состав чисел). Авторская разработка
Наглядность для 1-2 классов по математике Числовы домики (состав чисел). Авторская разработка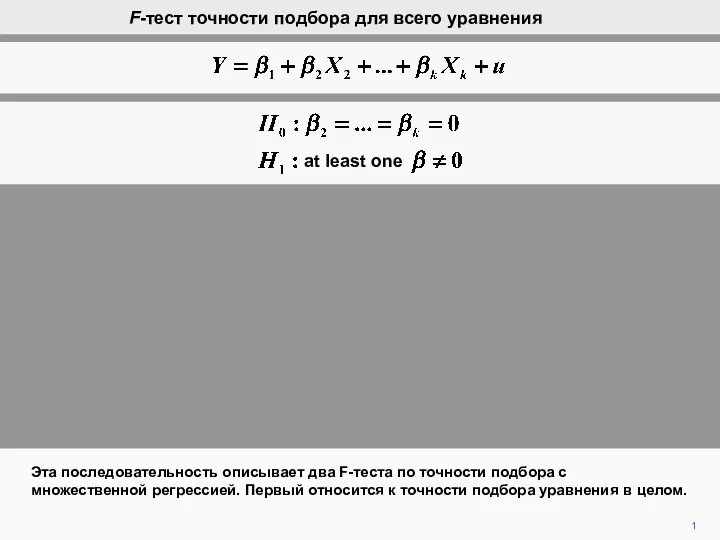 F-тест точности подбора для всего уравнения
F-тест точности подбора для всего уравнения Актеры Нижегородской области в числах и задачах. Евгений Евстигнеев и Валентина Теличкина
Актеры Нижегородской области в числах и задачах. Евгений Евстигнеев и Валентина Теличкина В світі кіл. Довжина кола
В світі кіл. Довжина кола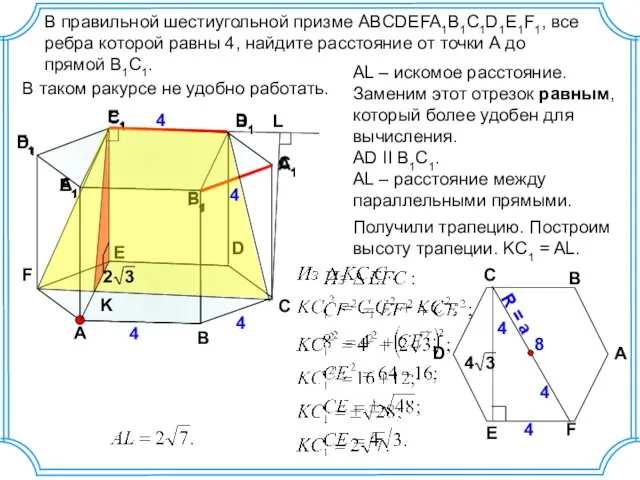 Правильная шестиугольная призма. (№25)
Правильная шестиугольная призма. (№25) Задачи на разностное сравнение.1кл.по программе Школа России
Задачи на разностное сравнение.1кл.по программе Школа России Методы решения систем уравнений. Критерий итерационной сходимости
Методы решения систем уравнений. Критерий итерационной сходимости В чем измеряется площадь земли
В чем измеряется площадь земли Многогранники. Выпуклые и невыпуклые многогранники
Многогранники. Выпуклые и невыпуклые многогранники Статистическая оценка параметров распределений
Статистическая оценка параметров распределений Задачи в готовых чертежах по теме: Признаки равенства треугольников
Задачи в готовых чертежах по теме: Признаки равенства треугольников Понятие множества и элемента множества. Способы задания множества
Понятие множества и элемента множества. Способы задания множества Живопись и математика
Живопись и математика Принятие решений при неполной информации. Классификация методов теории принятия решений
Принятие решений при неполной информации. Классификация методов теории принятия решений Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Окружность, круг, радиус, диаметр. 5 класс
Окружность, круг, радиус, диаметр. 5 класс