Содержание
- 2. Эллипс и его уравнение Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до
- 3. .
- 4. .
- 5. . − каноническое уравнение эллипса (b2=a2−c2). Если b=a, то уравнение примет вид: х2+у2 = а2 −
- 6. Если центр смещен в точку (х0; у0), то уравнение эллипса примет вид: a, b − полуоси
- 7. Построение эллипса по каноническому уравнению .
- 8. Гипербола и ее уравнение Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых
- 9. Выберем прямоугольную систему координат так же, как и в случае вывода уравнения эллипса. Тогда После преобразования
- 10. Если центр смещен в точку (х0; у0), то уравнение гиперболы примет вид: a − действительная полуось
- 11. Построение гиперболы по каноническому уравнению .
- 12. .
- 13. Парабола и ее уравнение Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и
- 14. Обозначив расстояние от фокуса до директрисы через p, получим координаты фокуса F(0;p/2). Пусть M(x; y) −
- 15. Уравнение параболы с вершиной, смещенной в точку (х0; у0), и осью симметрии, параллельной оси Оу (х=х0),
- 16. Построение параболы по каноническому уравнению .
- 17. Пример 1. Привести уравнение к каноническому виду и построить соответствующую линию .
- 18. Пример 2. Привести уравнение к каноническому виду и построить соответствующую линию .
- 20. Скачать презентацию

















 Урок математики в 1 классе по теме Знакомство с понятием Уравнение
Урок математики в 1 классе по теме Знакомство с понятием Уравнение Единицы измерения в разных странах
Единицы измерения в разных странах ГИА. Открытый банк заданий по математике. Задача
ГИА. Открытый банк заданий по математике. Задача Треугольник вписанный в окружность
Треугольник вписанный в окружность Свойства параллельных прямых
Свойства параллельных прямых Элементы теории вероятностей и математической статистики
Элементы теории вероятностей и математической статистики Симметрия вокруг нас
Симметрия вокруг нас ЕГЭ по математике. Вариант 1
ЕГЭ по математике. Вариант 1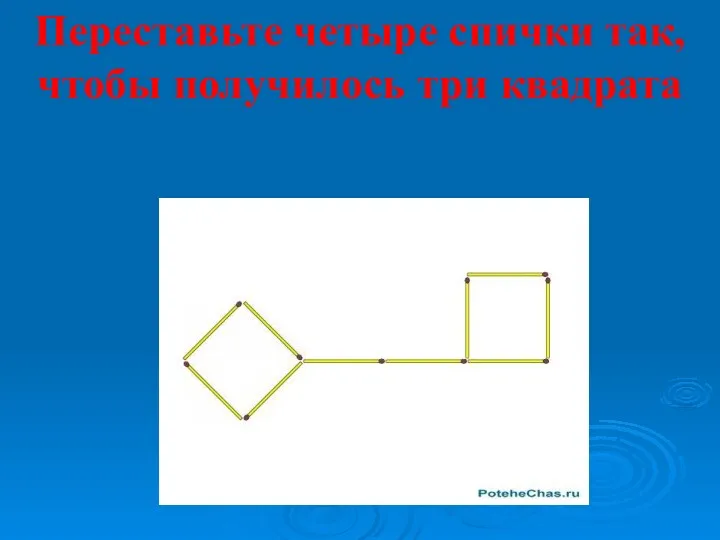 Игры со спичками
Игры со спичками Тетраэдр. Задания для устного счета. Упражнение 5
Тетраэдр. Задания для устного счета. Упражнение 5 Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Противоположные числа и модуль числа
Противоположные числа и модуль числа Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Площадь трапеции
Площадь трапеции Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций
Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Параллельные прямые
Параллельные прямые Презентация к мастер-классу Системно-деятельностный подход при решении задач
Презентация к мастер-классу Системно-деятельностный подход при решении задач Свойства прямоугольных треугольников. 7 класс
Свойства прямоугольных треугольников. 7 класс Виды симметрии. Центральная и осевая симметрия
Виды симметрии. Центральная и осевая симметрия Решение задач с применением диаграмм Эйлера-Венна
Решение задач с применением диаграмм Эйлера-Венна Тригонометрические уравнения. Отбор корней с помощью графиков
Тригонометрические уравнения. Отбор корней с помощью графиков Музыкальные инструменты для детей
Музыкальные инструменты для детей Практикум по решению ключевых типов задач по теории вероятностей. Часть 2. 11 класс
Практикум по решению ключевых типов задач по теории вероятностей. Часть 2. 11 класс Математическое моделирование автоматических систем регулирования
Математическое моделирование автоматических систем регулирования Регрессио́нный анализ. Примеры применения регрессионного анализа
Регрессио́нный анализ. Примеры применения регрессионного анализа Случаи сложения и вычитания, основанные на знании нумерации чисел
Случаи сложения и вычитания, основанные на знании нумерации чисел Решение систем уравнений способом сложения
Решение систем уравнений способом сложения