Содержание
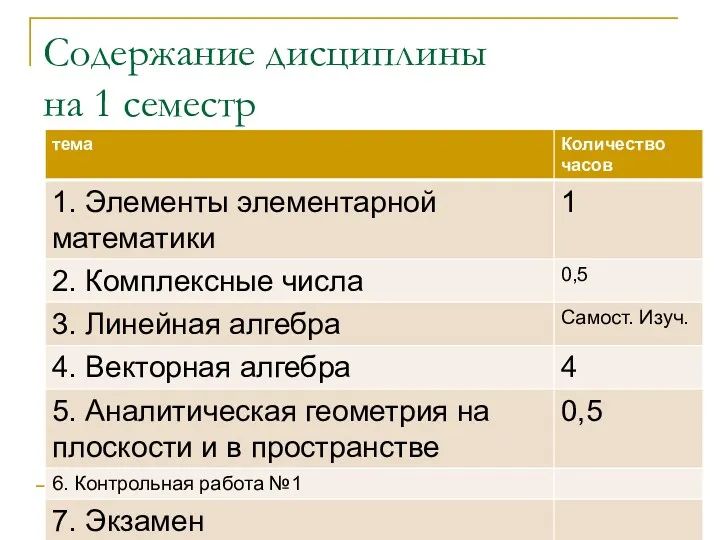
- 2. Содержание дисциплины на 1 семестр
- 3. Информационные источники Список литературы: Шипачев В.С. «Высшей математики» - М.: «Высшая школа», 2003. Шипачев В.С «Задачник
- 4. Информационные источники Список литературы (электронный формат) А.Б. Соболев, А.Ф. Рыбалко Математика: Курс лекций для технических вузов.
- 5. Образовательные ресурсы интернета Поисковая система Нигма – математика, Эл. адрес: http://nigma.ru; Высшая математика – просто и
- 6. Образовательные ресурсы интернета Образовательный проект А.Н. Варгина http://www.ph4s.ru/ Образовательные ресурсы Интернета - Математика. http://www.alleng.ru/
- 7. Программные приложения для математических вычислений Mathcad - система компьютерной алгебры (платная) ссылка на эл. ресурс http://www.ptc.com/products/mathcad/
- 8. Введение в математику Для того чтобы успешно решать задачи по высшей математике НЕОБХОДИМО: складывать, вычитать, умножать
- 9. 1. Элементы элементарной математики Вспоминаем, что дроби можно сокращать- (сократили на 2), (сократили на 5) (сократили
- 10. 2. Комплексные числа 2.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Определение. Комплексным числом z называется выражение , где a и
- 11. Определение. Числа и называются комплексно – сопряженными. Определение. Два комплексных числа и называются равными, если соответственно
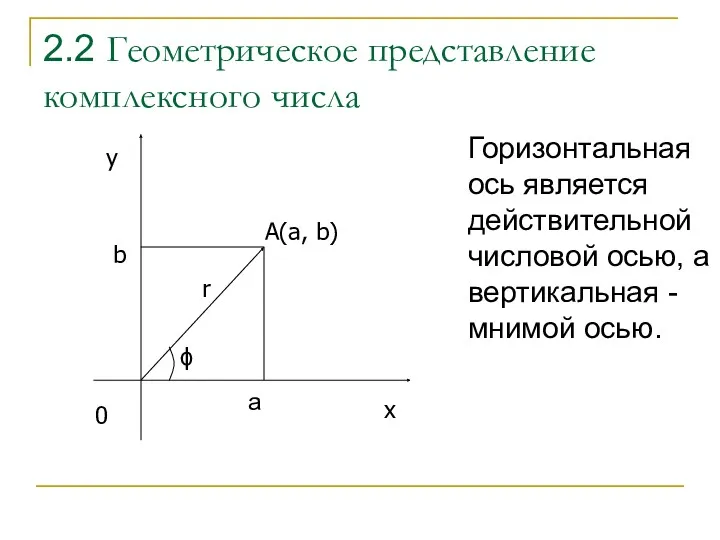
- 12. 2.2 Геометрическое представление комплексного числа Горизонтальная ось является действительной числовой осью, а вертикальная - мнимой осью.
- 13. 2.3 Тригонометрическая форма комплексного числа. Из геометрических соображений: Тогда комплексное число можно представить в виде: -
- 14. 2.4 Действия с комплексными числами. Основные действия с комплексными числами вытекают из действий с многочленами 1)
- 15. 2) Умножение В тригонометрической форме: В случае комплексно – сопряженных чисел:
- 16. 3) Деление. В тригонометрической форме:
- 17. 4) Возведение в степень. Из операции умножения: В общем случае: где n – целое положительное число.
- 18. 5) Извлечение корня из комплексного числа где к=0, 1, 2, …, n-1 Корень n – ой
- 19. 2.5 Показательная форма комплексного числа Уравнение Эйлера: Показательная форма к.ч.
- 20. 3. Линейная алгебра Самостоятельное изучение
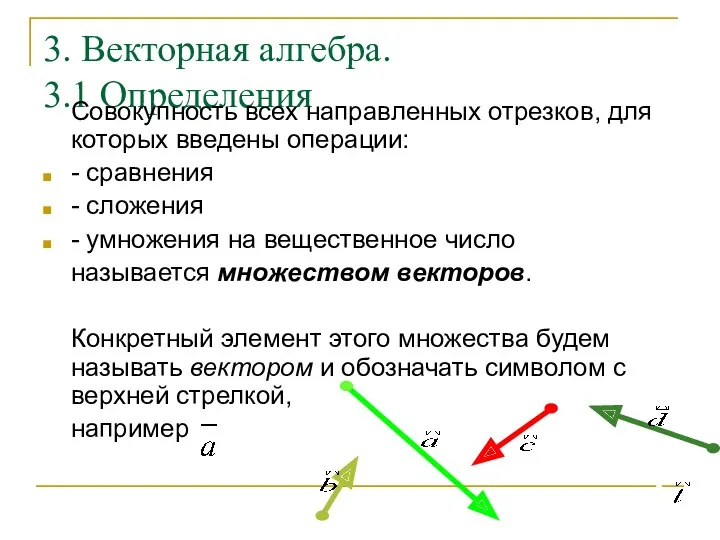
- 21. 3. Векторная алгебра. 3.1 Определения Совокупность всех направленных отрезков, для которых введены операции: - сравнения -
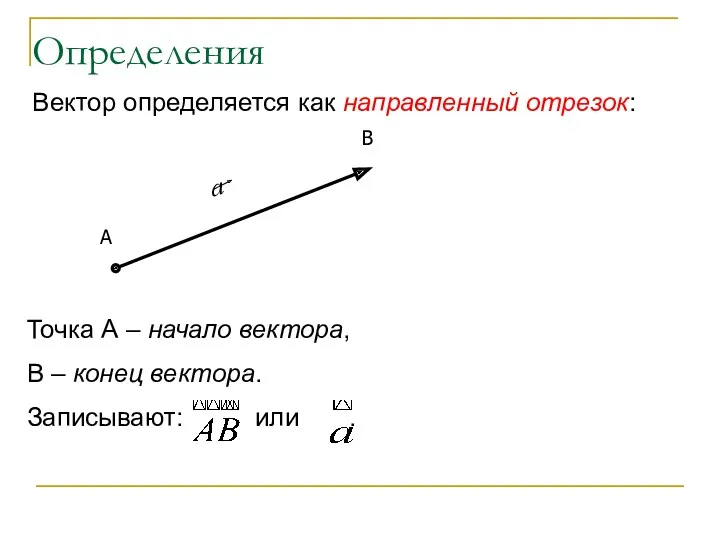
- 22. Определения Вектор определяется как направленный отрезок: Точка А – начало вектора, В – конец вектора. Записывают:
- 23. Определения Направленный отрезок, начало и конец которого совпадают, называется нулевым направленным отрезком. Длиной (модулем) вектора называется
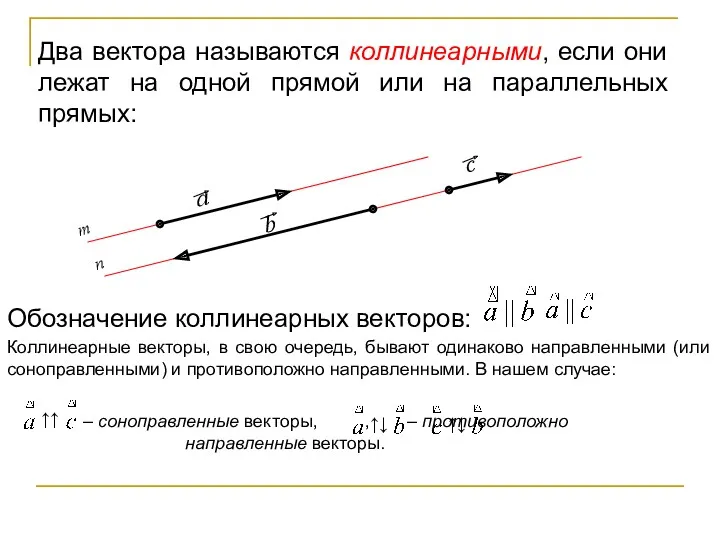
- 24. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых: Коллинеарные векторы,
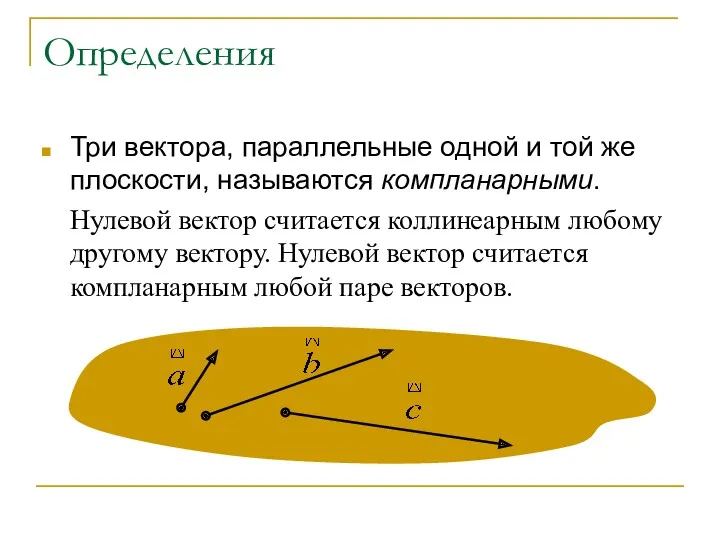
- 25. Определения Три вектора, параллельные одной и той же плоскости, называются компланарными. Нулевой вектор считается коллинеарным любому
- 26. Определения Два вектора называются равными, если: 1) они соноправлены; 2) их модули равны, т.е.
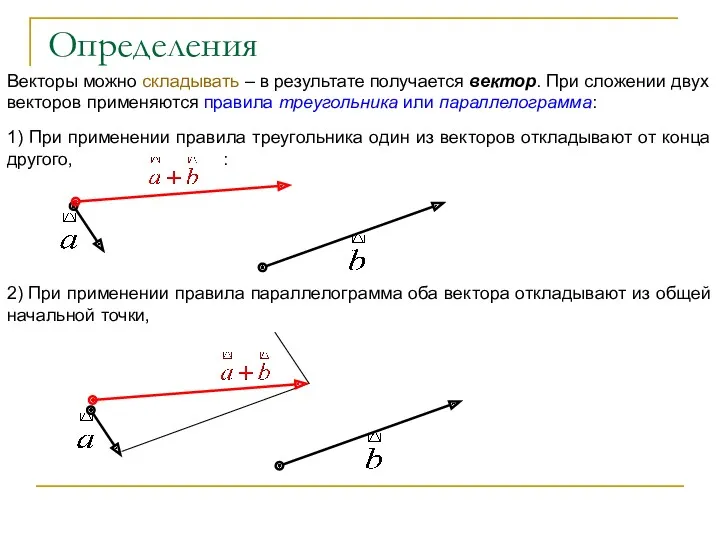
- 27. Векторы можно складывать – в результате получается вектор. При сложении двух векторов применяются правила треугольника или
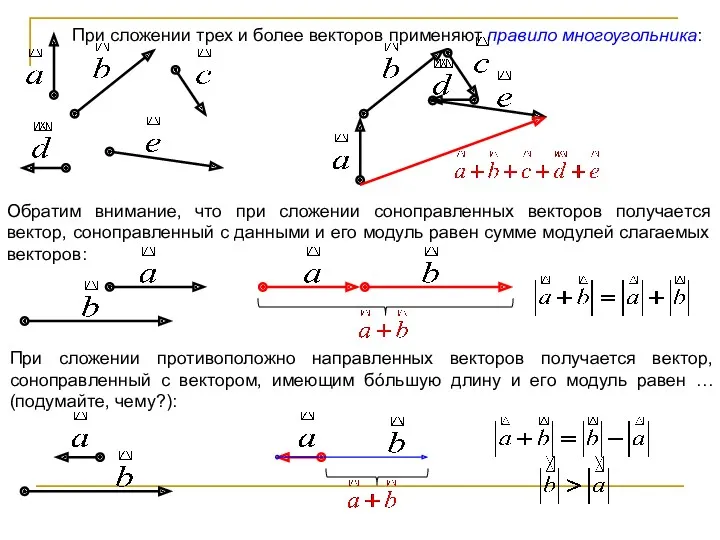
- 28. При сложении трех и более векторов применяют правило многоугольника: Обратим внимание, что при сложении соноправленных векторов
- 29. Сложение векторов, как и сложение чисел подчиняется законам: Следующее действие с векторами – умножение вектора на
- 30. Линейная зависимость векторов Определение. Выражение вида , где некоторые числа, называется линейной комбинацией векторов
- 31. Линейная зависимость векторов Определение. Векторы называются линейно зависимыми, если существует их нетривиальная линейная комбинация Определение. Векторы
- 32. Базис в пространстве векторов Определение: Базисом в пространстве векторов называется набор линейно независимых векторов
- 33. Базис в пространстве векторов Определение Базисом на прямой называется любой ненулевой вектор, принадлежащий этой прямой. m
- 34. Базис в пространстве векторов Определение Базисом на плоскости называется любая упорядоченная пара линейно независимых векторов, принадлежащих
- 35. Координаты вектора: Пусть дан базис тогда любой вектор в пространстве может быть представлен, и притом единственным
- 36. Координаты вектора: Для записи вектора в координатном представлении используются формы:
- 37. Операции с векторами в координатном представлении: Сравнение векторов: Два вектора и равны тогда и только тогда,
- 38. Условия линейной зависимости и независимости векторов в координатном представлении Для того чтобы два вектора на плоскости
- 39. Условия линейной зависимости и независимости векторов в координатном представлении Для того чтобы три вектора в пространстве
- 40. Замечание: Равенства и соответственно являются необходимыми и достаточными условиями коллинеарности пары векторов на плоскости и компланарности
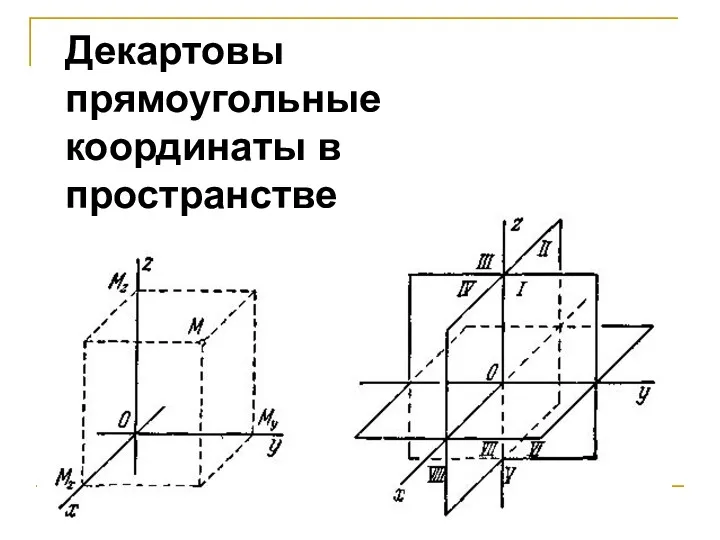
- 41. Декартова система координат. Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется
- 42. Декартовы прямоугольные координаты в пространстве
- 43. Основные формулы: Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то координаты вектора определяются по
- 44. Основные формулы: Если точка М(х, у, z) делит отрезок АВ в соотношении λ/μ, считая от А,
- 45. Скалярное произведение векторов. Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на
- 46. Формула для вычисления угла между векторами:
- 47. Свойства скалярного произведения векторов 1) = ⎪ ⎪2; 2) ⋅ = 0, если ⊥ или =
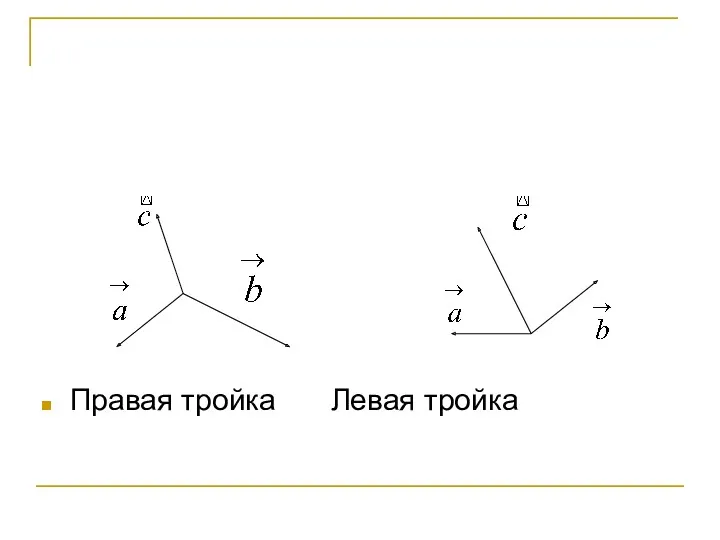
- 48. Векторное произведение векторов. Три некомпланарных вектора взятые в указанном порядке образуют правую тройку, если с конца
- 49. Правая тройка Левая тройка
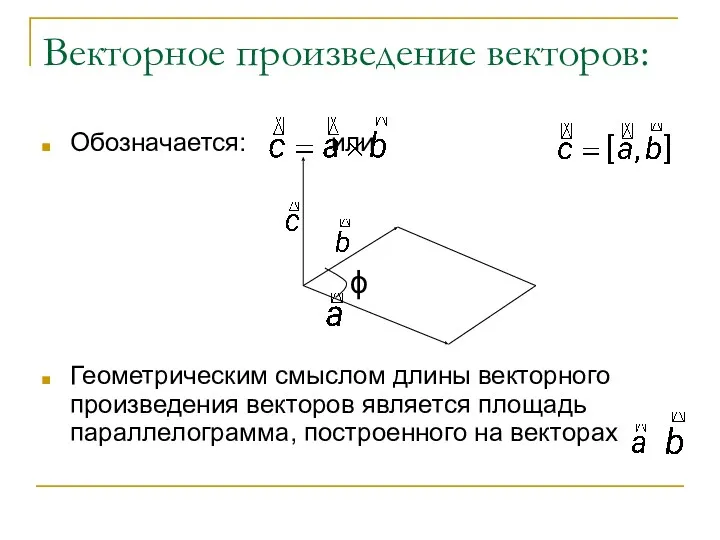
- 50. Векторное произведение векторов. Векторным произведением векторов и называется вектор удовлетворяющий следующим условиям: 1) где ϕ -
- 51. Векторное произведение векторов: Обозначается: или Геометрическим смыслом длины векторного произведения векторов является площадь параллелограмма, построенного на
- 52. Свойства векторного произведения векторов: 1) ; 2) , если ⎪⎪ или = 0 или = 0;
- 53. Векторное произведение векторов Если заданы векторы (xa, ya, za) и (xb, yb, zb) = в декартовой
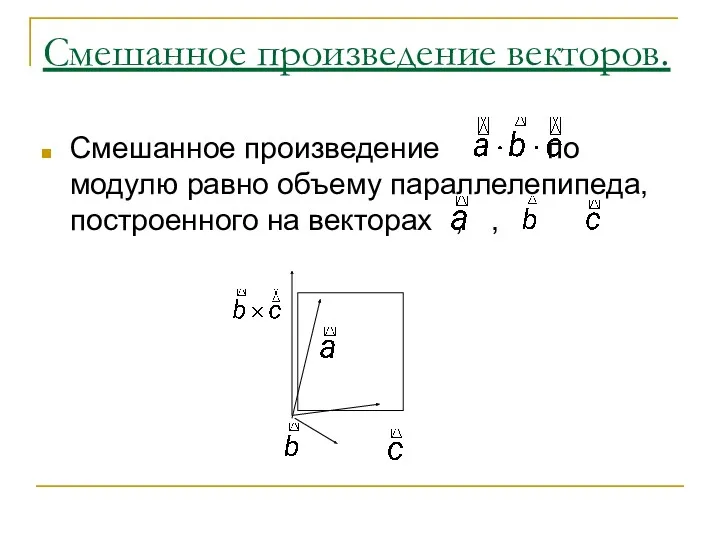
- 54. Смешанное произведение векторов. Определение. Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на
- 55. Смешанное произведение векторов. Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , ,
- 56. Свойства смешанного произведения векторов. 1)Смешанное произведение равно нулю, если: а) хоть один из векторов равен нулю;
- 57. Свойства смешанного произведения векторов: 6) Если , то
- 58. 5. Аналитическая геометрия на плоскости и в пространстве Математический форум Math Help Planet Эл. адрес http://mathhelpplanet.com
- 59. Произведение вектора на число
- 60. Произведение вектора на число При движении с постоянной скоростью v перемещение s за время t выражается
- 62. Скачать презентацию















































 Введение в методологию CFD
Введение в методологию CFD Что такое координаты. 6 класс
Что такое координаты. 6 класс Веселая арифметика
Веселая арифметика Статистика. Предмет метод и задачи
Статистика. Предмет метод и задачи Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Работа с интерактивной доской.
Работа с интерактивной доской. Округление десятичных дробей. Урок математики в 5 классе
Округление десятичных дробей. Урок математики в 5 классе Базовые компоненты эконометрики
Базовые компоненты эконометрики Задание для детей по ФЭМП с использованием слайдов.
Задание для детей по ФЭМП с использованием слайдов. Статистика. Понятие, предмет и метод статистики. (Лекция 1)
Статистика. Понятие, предмет и метод статистики. (Лекция 1) Презентация Устный счёт 2 класс 1 четверть № 1
Презентация Устный счёт 2 класс 1 четверть № 1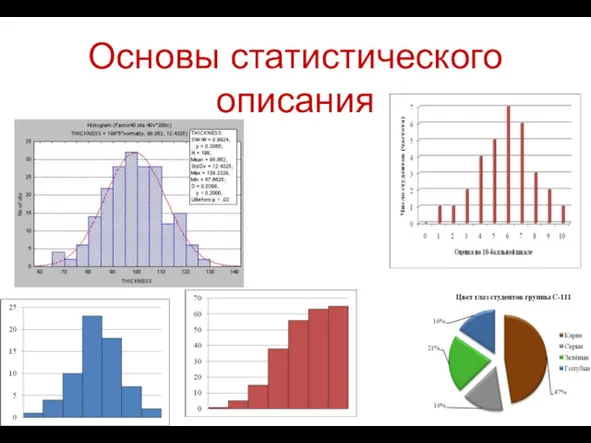 Основы статистического описания
Основы статистического описания Презентация 1 класс. Занимательная математика.
Презентация 1 класс. Занимательная математика. Математическая игра для 5 класса Зажги салют!
Математическая игра для 5 класса Зажги салют! Царстве математики. 6 класс
Царстве математики. 6 класс Обобщение и систематизация знаний по теме Углы и многоугольники
Обобщение и систематизация знаний по теме Углы и многоугольники Предел функции. Пределы с неопределенностью вида и метод их решения
Предел функции. Пределы с неопределенностью вида и метод их решения Рациональные числа и действия над ними. 6 класс
Рациональные числа и действия над ними. 6 класс Деление десятичных дробей на натуральные числа
Деление десятичных дробей на натуральные числа Презентация для учащихся 2 класса Устный счёт с Дедом Морозом и Снегурочкой
Презентация для учащихся 2 класса Устный счёт с Дедом Морозом и Снегурочкой Презентация игры Математическое дерево
Презентация игры Математическое дерево Математика 2 класс. Сложение и вычитание чисел в пределах 100. Дидактическая игра Ромашки для кошки
Математика 2 класс. Сложение и вычитание чисел в пределах 100. Дидактическая игра Ромашки для кошки Урок математики во 2 классе по теме Трёхзначные числа (Гармония)
Урок математики во 2 классе по теме Трёхзначные числа (Гармония) Туынды. Алғашқы функция. Интеграл
Туынды. Алғашқы функция. Интеграл Решение текстовых задач на все арифметические действия
Решение текстовых задач на все арифметические действия Умножение десятичных дробей. Тренажер
Умножение десятичных дробей. Тренажер 20231106_prilozhenie_no1
20231106_prilozhenie_no1 Теорема Виета. Урок 78. 8 класс
Теорема Виета. Урок 78. 8 класс