Содержание
- 2. Лекция № 1 §1. Комплексные числа и последовательности комплексных чисел. п. 1. Понятие комплексного числа. Геометрическая
- 3. Немного истории Комплексные числа вошли в математику в XVI в. как корни квадратного уравнения с отрицательным
- 4. Как понимать? Что делать?
- 5. Вначале такие корни отбрасывались, как «невозможные», «мнимые», и появление их считалось признаком отсутствия решения у задачи,
- 6. Обоснование: мнимые корни не выражают величины, так как их нельзя сравнивать друг с другом, нельзя сказать,
- 7. Однако позже было обнаружено, что над ними можно производить четыре алгебраических действия, причем сохраняются свойства, присущие
- 8. Это и послужило основанием называть мнимые корни числами («Алгебра» итальянского инженера Р. Бомбелли, 1572 г.).
- 9. Геометрическое изображение комплексных чисел в виде точек или векторов "на плоскости" было введено в 1799 г.
- 10. Символ i для мнимой единицы ввел в 1777 г. Л. Эйлер (1707— 1783). Термин «комплексное число»
- 11. Большое значение в раскрытии важной роли комплексных чисел в математике имели работы Л. Эйлера и К.
- 12. До появления этой теоремы можно было бы ожидать, что, подобно тому как квадратное уравнение привело к
- 13. Геометрическое изображение комплексного числа как точки или вектора на плоскости, естественно, приводит к мысли построить дальнейшие
- 14. Однако поиски числовой системы, зависящей от трех единиц: 1, i, j, геометрически изображаемой с помощью точек
- 15. В 1843 т. английский математик У. Гамильтон (1805—1865) показал, что можно построить числовые системы, зависящие от
- 16. Вообще, гиперкомплексными числами ранга п называются «числа» вида — единицы, —действительные числа, когда указаны правила алгебраических
- 17. Однако К. Вейерштрасс показал, что при п > 2 нельзя сохранить все свойства, присущие алгебраическим действиям
- 18. Немецкий математик Ф. Фробениус (1849—1917) доказал, что, даже отказавшись от переместительного закона умножения, можно сохранить остальные
- 19. -вектор Определим операцию сложения: операцию умножения на число: базис Рассмотрим плоскость R2.
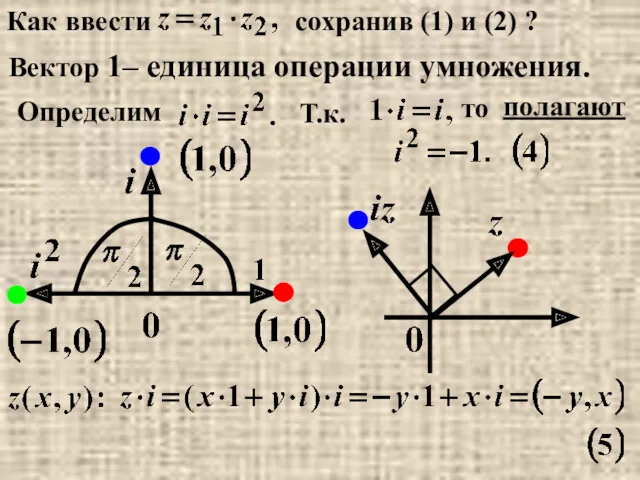
- 20. Как ввести сохранив (1) и (2) ? Вектор 1– единица операции умножения. Определим Т.к. то полагают
- 21. Правило умножения Def. Числовая плоскость называется комплексной плоскостью C, если для ее точек определены модули (1),
- 22. Действительные числа включаются в множество комплексных чисел. a=(a,0)-вещественное число, -1=(-1, 0), i =(0, 1)- мнимая единица,
- 23. Деление. Комплексное сопряжение.
- 24. Примеры.
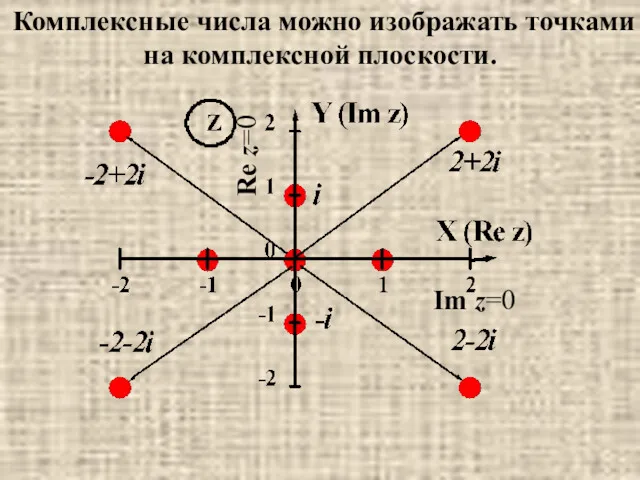
- 25. Комплексные числа можно изображать точками на комплексной плоскости. Im z=0 Re z=0
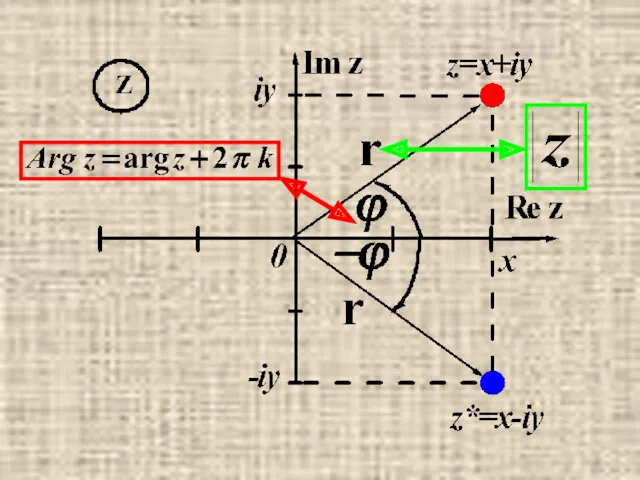
- 27. Модуль и аргумент комплексного числа Полярные координаты (x,y)↔(r,ϕ). Модуль комплексного числа: Аргумент комплексного числа: Главное значение
- 28. -разрез по - PC Soft -разрез по -литература Примеры. — не определен!
- 29. Тригонометрическая форма записи формула Эйлера: Показательная форма записи Теорема. Пусть тогда
- 30. Примеры.
- 31. Вопрос. Умножение и деление в показательной форме. Формула Муавра.
- 32. Извлечение корня. Корень n-той степени из комплексного числа принимает n различных значений.
- 33. Примеры.
- 37. Операция сравнения в С не определена. Множество комплексных чисел C образует поле. Поле С не является
- 38. Неравенства треугольника. Упорядоченная четверка является нормированным векторным пространством над полем R. Оно превратится в метрическое пространство,
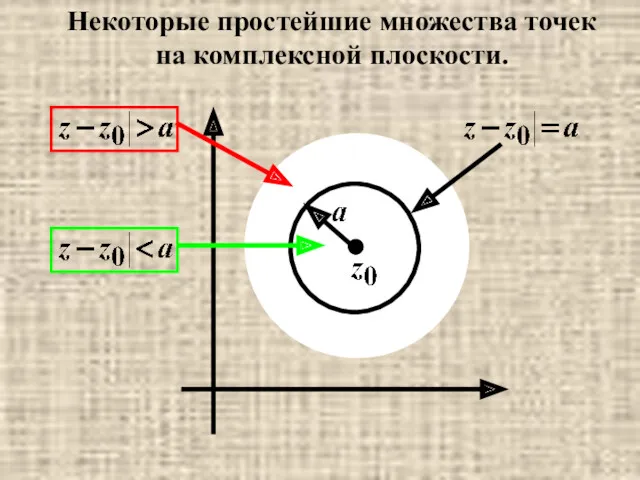
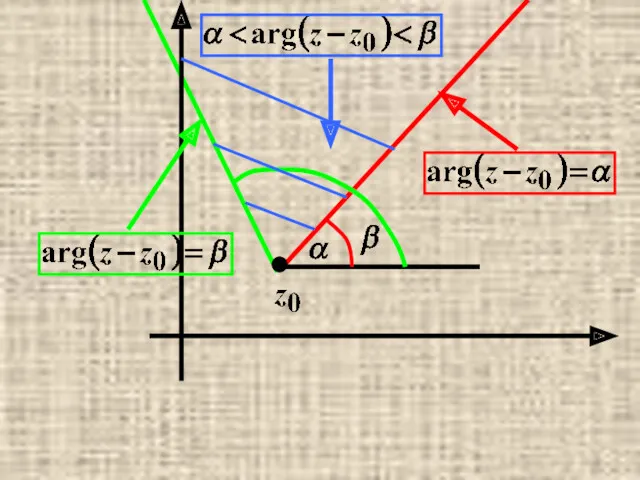
- 39. Некоторые простейшие множества точек на комплексной плоскости.
- 42. Скачать презентацию


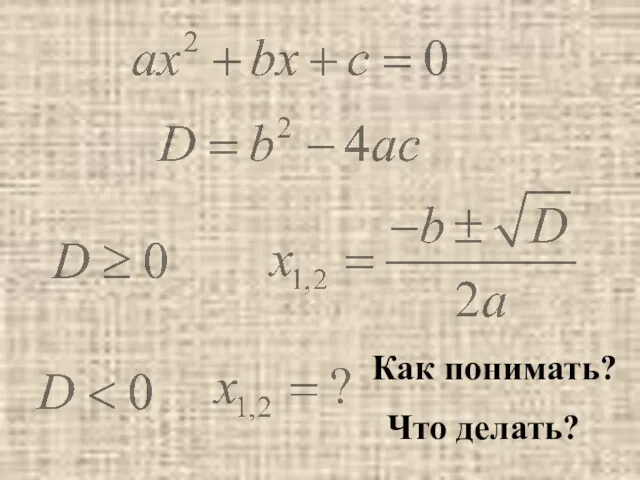






















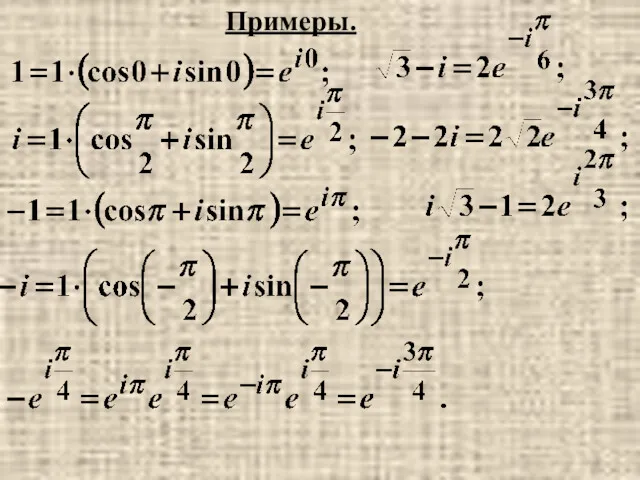



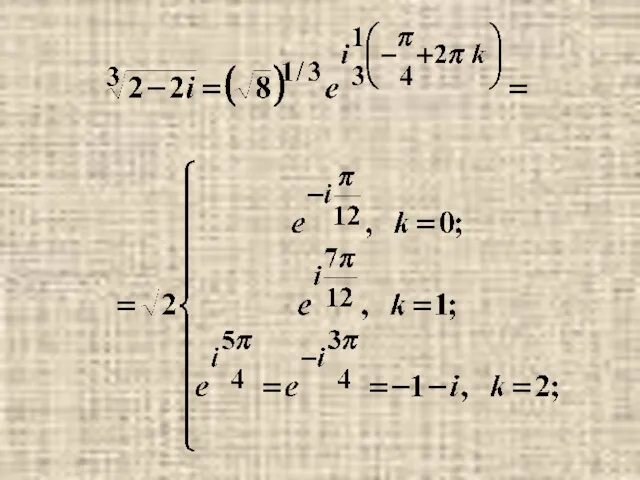
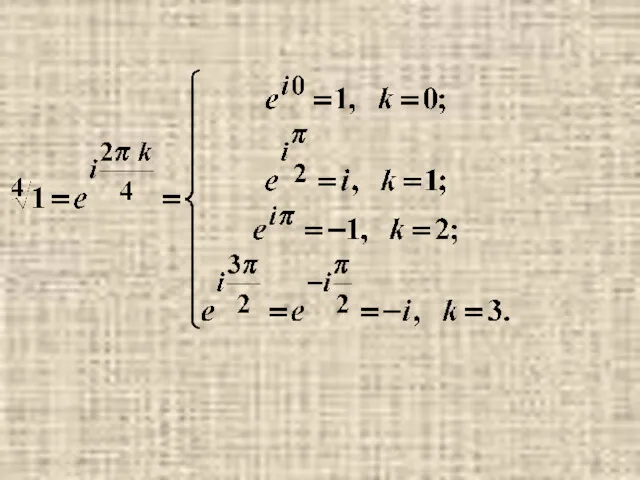
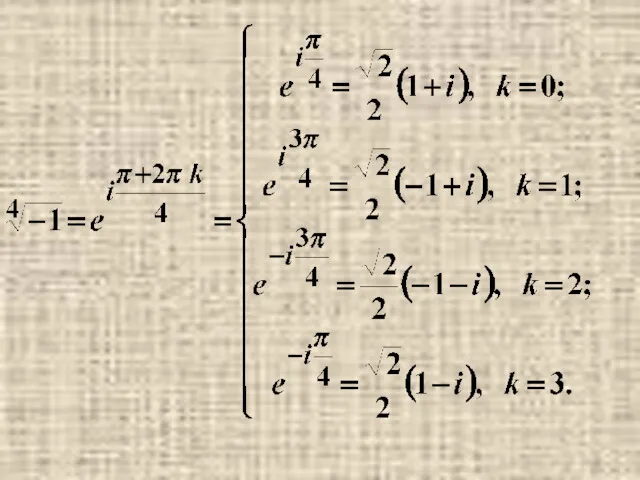


 Подготовка к ЕГЭ по математике. Решение заданий В3
Подготовка к ЕГЭ по математике. Решение заданий В3 Единицы измерения времени: час и минута
Единицы измерения времени: час и минута Правильные многоугольники
Правильные многоугольники Направления и наклоны. Введение. (Модуль 1)
Направления и наклоны. Введение. (Модуль 1) Вправи на додавання і віднімання в межах 20. Задачі на знаходження невідомого доданка (урок 68)
Вправи на додавання і віднімання в межах 20. Задачі на знаходження невідомого доданка (урок 68) Единицы времени (2 класс)
Единицы времени (2 класс) Длина окружности
Длина окружности Системно-деятельностный подход. Урок математики в 3 классе Деление с остатком с презентацией
Системно-деятельностный подход. Урок математики в 3 классе Деление с остатком с презентацией 01-Формула суммы п первых членов арифметической прогрессии
01-Формула суммы п первых членов арифметической прогрессии Игра-презентация Формирование представлений о красном цвете
Игра-презентация Формирование представлений о красном цвете Чи такі вони прості ці прості числа?
Чи такі вони прості ці прості числа? Виды углов
Виды углов МБДОУ Детский сад комбинированного випа № 70 Использование дидактических игр в развитии математических представлений
МБДОУ Детский сад комбинированного випа № 70 Использование дидактических игр в развитии математических представлений Старинные меры измерения длины
Старинные меры измерения длины Решение примеров и задач в пределах 20, 1 класс
Решение примеров и задач в пределах 20, 1 класс Понятие о производной функции, её геометрический и физический смысл. Производные элементарных функций
Понятие о производной функции, её геометрический и физический смысл. Производные элементарных функций Математические модели
Математические модели Раскрытие скобок и заключение в скобки
Раскрытие скобок и заключение в скобки Числовые последовательности. Занимательная математика
Числовые последовательности. Занимательная математика Математика в лицах. Великие математики
Математика в лицах. Великие математики Устный счет Помоги пчелке
Устный счет Помоги пчелке Методы анализа данных. Примеры задач. Иллюстрации
Методы анализа данных. Примеры задач. Иллюстрации урок математики 1 класс Масса
урок математики 1 класс Масса Прямоугольный параллелепипед
Прямоугольный параллелепипед Векторы на плоскости. Работа по геометрии
Векторы на плоскости. Работа по геометрии Предел функции
Предел функции Урок по математике Название компонентов и результата деления.
Урок по математике Название компонентов и результата деления. Правильные многоугольники
Правильные многоугольники