ГОЛОВНІ ОСІ ТА ГОЛОВНІ МОМЕНТИ ІНЕРЦІЇ
Отримані залежності показують, що при зміні
кута повороту осей значення моментів інерції змінюються, при цьому сума осьових моментів інерції залишається постійною.
Це означає, що можна визначити таке положення осей, при якому один з осьових моментів досягає максимального значення, а інший - відповідно мінімального значення.
Максимальні та мінімальні осьові моменти інерції називаються головними
моментами інерції, а осі, щодо яких вони обчислюються, - головними осями.
Для визначення положення головних осей досить прирівняти до нуля першу похідну
осьового моменту інерції по куту повороту:
Отриманий результат показує, що для шуканого положення осей відцентровий момент перетворюється в нуль.
Звідси можна знайти положення головних осей:
Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає два положення осей, що відрізняються один від одного на 900.
Таким чином, обидві головні осі взаємно перпендикулярні.













 Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Тесты по математике 2 классЧисла от 1 до 100
Тесты по математике 2 классЧисла от 1 до 100 Образование чисел из одного десятка и нескольких единиц
Образование чисел из одного десятка и нескольких единиц Векторы в пространстве
Векторы в пространстве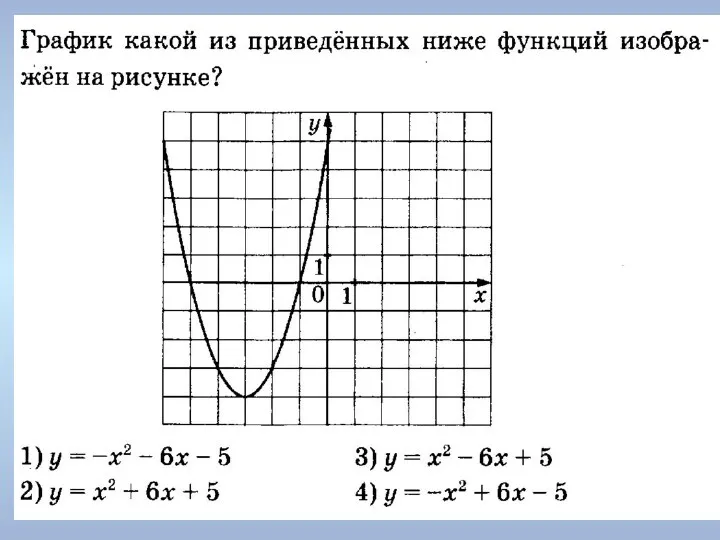 Графики. Парабола
Графики. Парабола Интерактивная игра по математике Собирай урожай
Интерактивная игра по математике Собирай урожай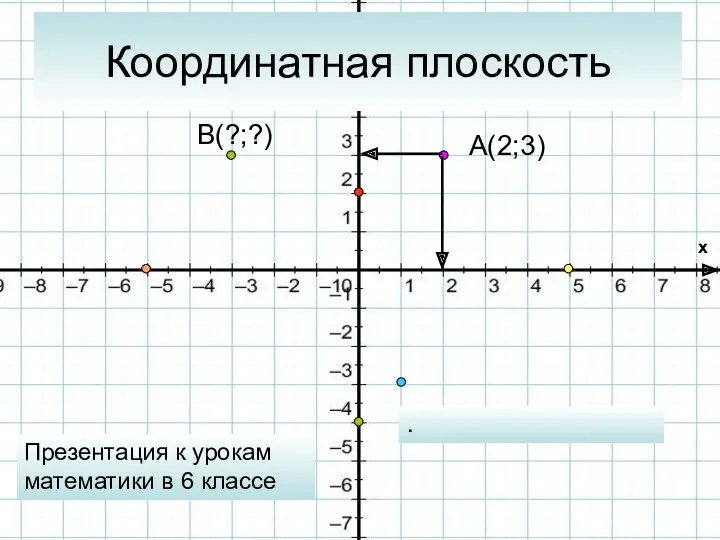 Координатная плоскость
Координатная плоскость Презентация к уроку математики по теме Умножение многозначных чисел на однозначное. 3 класс.
Презентация к уроку математики по теме Умножение многозначных чисел на однозначное. 3 класс. Делимое, делитель, частное
Делимое, делитель, частное Деление на 2. 2 класс
Деление на 2. 2 класс Таблица умножения. 3 класс.
Таблица умножения. 3 класс. Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Решение линейных и квадратных уравнений. 9 класс
Решение линейных и квадратных уравнений. 9 класс Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Задание 13 расстояние от точки до плоскости. Примеры решения задач
Задание 13 расстояние от точки до плоскости. Примеры решения задач Неравенства второй степени с одной переменной
Неравенства второй степени с одной переменной Наибольший общий делитель и наименьшее общее кратное чисел
Наибольший общий делитель и наименьшее общее кратное чисел Треугольник и его виды
Треугольник и его виды Физико–математический турнир для учащихся 10-11 классов
Физико–математический турнир для учащихся 10-11 классов Решения систем линейных уравнений. Метод подстановки и метод сложения. 7 класс
Решения систем линейных уравнений. Метод подстановки и метод сложения. 7 класс Презентация Вычитание. Название компонентов и результат действия
Презентация Вычитание. Название компонентов и результат действия Умножение и деление натуральных чисел. 5 класс
Умножение и деление натуральных чисел. 5 класс Интегрированные задачи. Математика + история. 8 класс
Интегрированные задачи. Математика + история. 8 класс Свойство умножения
Свойство умножения Презентация Способы прибавления и вычитания числа 4
Презентация Способы прибавления и вычитания числа 4 Додавання і віднімання числа 3. Переставний закон додавання. Урок №38. Математика
Додавання і віднімання числа 3. Переставний закон додавання. Урок №38. Математика Задачи со спичками
Задачи со спичками Методы решения тригонометрических уравнений. (Урок-лекция)
Методы решения тригонометрических уравнений. (Урок-лекция)