Содержание
- 2. Сеть Ориентированный граф G с пропускными способностями дуг u: E(G)→ R+ и две выделенные вершины s
- 3. Поток Определение 6.1. Дан орграф G с пропускными способностями (вместимостями) u: E(G) → R+, потоком называется
- 4. s-t-Поток Дана сеть (G, u, s, t), s-t-потоком называется поток, удовлетворяющий закону сохранения во всех вершинах
- 5. Задача «Максимальный Поток» Дано: Сеть (G, u, s, t). Найти s-t-поток максимальной величины.
- 6. s-t-Разрез s-t-разрез в графе ― разрез δ(X) для некоторого X ⊂V(G) с s ∈ X и
- 7. s-t-Поток и s-t-разрез Лемма 6.2 Для всех A ⊆ V(G) таких, что s ∈ A, t
- 8. Доказательство (а)
- 9. s-t-Поток и s-t-разрез Лемма 6.2 Для всех A ⊆ V(G) таких, что s ∈ A, t
- 10. Обратные дуги и остаточные пропускные способности Определение 6.3 Для орграфа G определим Ğ:=(V(G), E(G)U{ĕ: e ∈E(G)}),
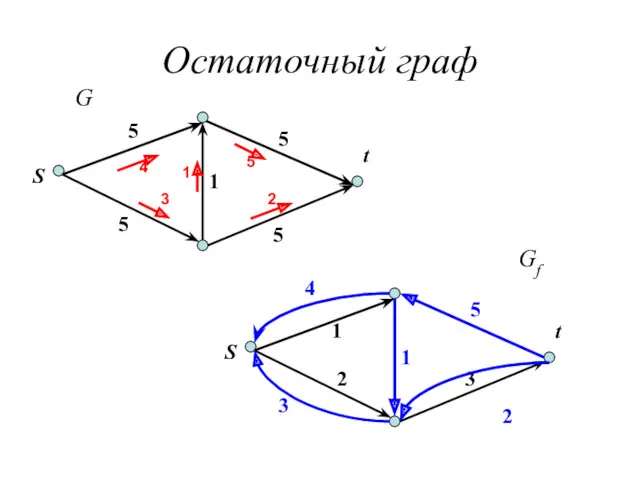
- 11. Остаточный граф S t 5 5 5 5 1 4 3 2 5 1 S t
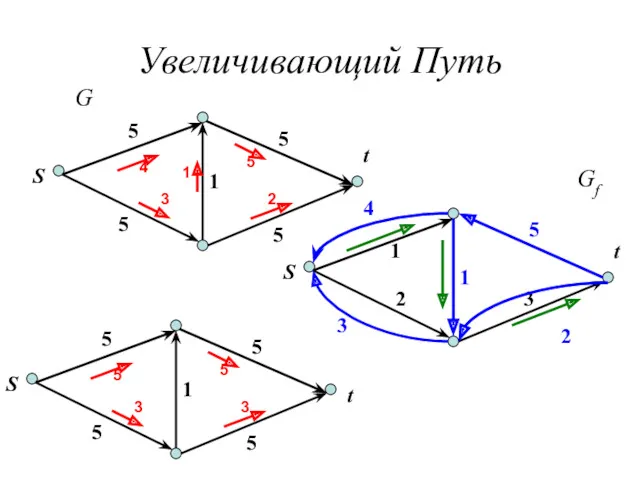
- 12. Увеличивающий Путь Даны поток f и путь (или цикл) P в Gf , увеличение f вдоль
- 13. Увеличивающий Путь S t 5 5 5 5 1 4 3 2 5 1 S t
- 14. Алгоритм Форда-Фалкерсона Input: Сеть (G, u, s, t). Output: s-t-поток f максимальной величины. Положим f(e) =
- 15. Замечание Найти увеличивающий путь легко (любой s-t-путь в Gf). Если выбирать произвольный увеличивающий путь в Gf
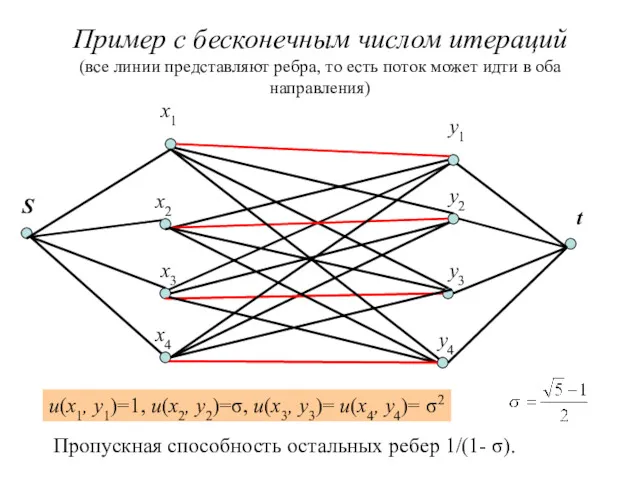
- 16. Пример c бесконечным числом итераций (все линии представляют ребра, то есть поток может идти в оба
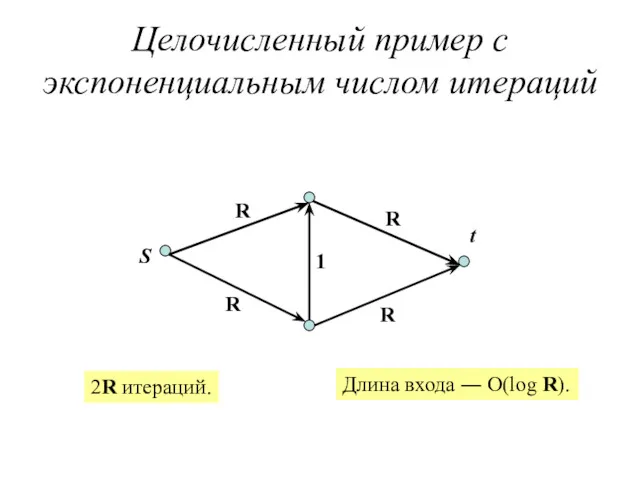
- 17. Упражнение 6.1 Показать, что для сети из предыдущего примера алгоритм Форда-Фалкерсона может работать бесконечно долго.
- 18. Целочисленный пример c экспоненциальным числом итераций S t R R R R 1 2R итераций. Длина
- 19. Характеризация максимального потока Теорема 6.4 s-t-Поток f является максимальным тогда и только тогда, когда в Gf
- 20. Доказательство Пусть в Gf не существует f-увеличивающего пути. ⇒ t не достижимо в Gf из s.
- 21. Замечание В частности, из доказательства следует, что каждому максимальному потоку соответствует s-t-разрез, пропускная способность которого равна
- 22. Максимальный поток и минимальный разрез Теорема 6.5 (Форд, Фалкерсон [1956], Элиас, Файнштайн, Шэннон [1956] ) Величина
- 23. Теорема о целочисленном потоке Следствие 6.6 Если пропускные способности дуг в сети целые числа, то существует
- 24. Упражнение 6.2 Поcтроить пример сети, в которой вместимости дуг целые числа, и существует нецелочисленный максимальный поток.
- 25. Теорема о Декомпозиции Потока Теорема 6.7 (Фалкерсон [1962] ) Пусть (G, u, s, t) ― сеть
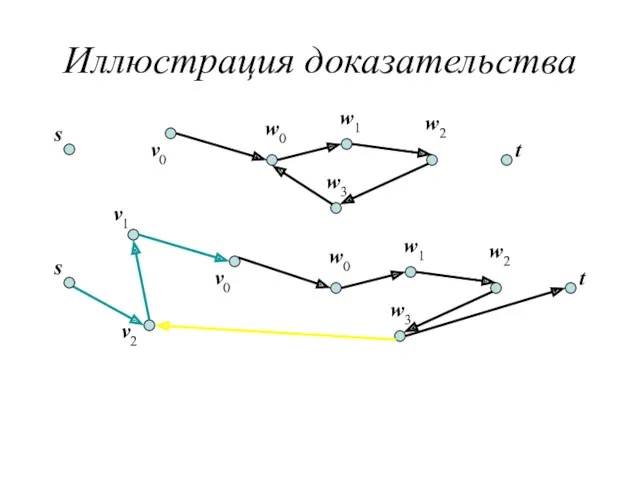
- 26. Доказательство Построим P , C и w индукцией по числу дуг с ненулевым потоком. Пусть e=(v0,w0)
- 27. Иллюстрация доказательства t s v0 w0 w1 w2 w3 t s v0 w0 w1 w2 w3
- 28. Доказательство Пусть P будет цикл или путь, найденный в результате описанной процедуры. w(P) = mine∈ E(P)
- 29. Теорема о Декомпозиции Потока Теорема 6.7 (Фалкерсон [1962] ) Пусть (G, u, s, t) ― сеть
- 31. Скачать презентацию






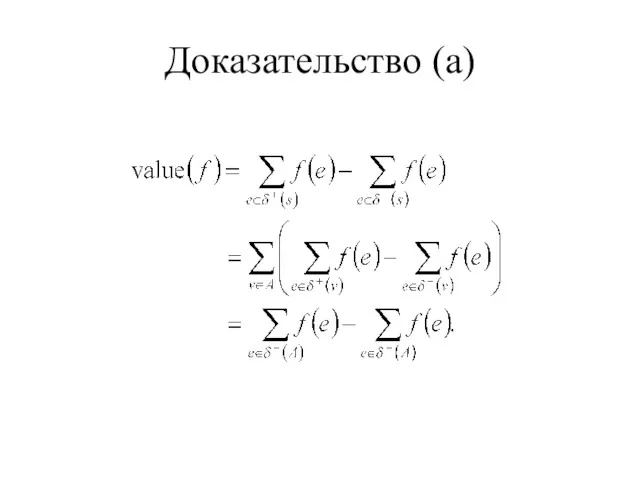









![Максимальный поток и минимальный разрез Теорема 6.5 (Форд, Фалкерсон [1956],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/159084/slide-21.jpg)


![Теорема о Декомпозиции Потока Теорема 6.7 (Фалкерсон [1962] ) Пусть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/159084/slide-24.jpg)


![Теорема о Декомпозиции Потока Теорема 6.7 (Фалкерсон [1962] ) Пусть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/159084/slide-28.jpg)
 Смежные и вертикальные углы. Решение задач
Смежные и вертикальные углы. Решение задач Представление результатов измерений. Неопределённость в измерениях
Представление результатов измерений. Неопределённость в измерениях Ознайомлення з дією множення
Ознайомлення з дією множення Считаем до 10. Тренажёр 1 класс
Считаем до 10. Тренажёр 1 класс Презентация к уроку математики во 2 классе на тему Контрольная работа
Презентация к уроку математики во 2 классе на тему Контрольная работа Алгоритм решения задач на нахождение слагаемых по сумме и разности
Алгоритм решения задач на нахождение слагаемых по сумме и разности Прибавить и вычесть 1.Веселое путешествие
Прибавить и вычесть 1.Веселое путешествие Віднімання натуральних чисел. Властивості віднімання
Віднімання натуральних чисел. Властивості віднімання Занимательный материал №3
Занимательный материал №3 Математические ребусы
Математические ребусы Устный счёт 4 класс
Устный счёт 4 класс презентация .по математике Единица времени. Час
презентация .по математике Единица времени. Час Решение задач
Решение задач Сложение и вычитание многочленов
Сложение и вычитание многочленов Математика. 4 класс.Прием письменного деления многозначных чисел на однозначное число.
Математика. 4 класс.Прием письменного деления многозначных чисел на однозначное число. Организация современного урока математики в условиях реализации ФГОС
Организация современного урока математики в условиях реализации ФГОС Презентация к уроку математике Присчитывание и отсчитывание по 1 по программе Гармония
Презентация к уроку математике Присчитывание и отсчитывание по 1 по программе Гармония Геометрические преобразования пространства
Геометрические преобразования пространства Все действия с десятичными дробями
Все действия с десятичными дробями Координатная плоскость
Координатная плоскость Анализ геометрической формы предмета
Анализ геометрической формы предмета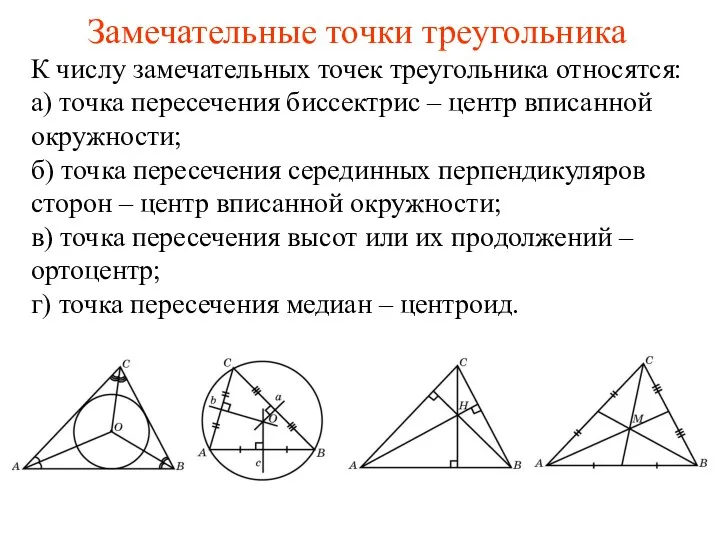 Замечательные точки в треугольнике
Замечательные точки в треугольнике Сложение и вычитание десятичных дробей. Урок 111
Сложение и вычитание десятичных дробей. Урок 111 Кратные и криволинейные интегралы
Кратные и криволинейные интегралы Сантиметр
Сантиметр Определенный интеграл как функция верхнего предела
Определенный интеграл как функция верхнего предела Среднее арифметическое
Среднее арифметическое Меры объема. Методика преподавания математики
Меры объема. Методика преподавания математики