Содержание
- 2. ЗМІСТ Рівномірний розподіл Нормальний розподіл (розподіл Гаусса) Розподіл “х - квадрат” Розподіл Стьюдента
- 3. Рівномірний розподіл Рівномірний розподіл. Розподіл ймовірностей називають рівномірним, якщо на проміжку (а,в), до якого належать всі
- 4. Рівномірний розподіл Звідси Але, як відомо З порівняння цих рівностей отримаємо: рис.1 рис.2
- 5. Рівномірний розподіл Отже щільність ймовірностей неперервної випадкової величини Х, яка рівномірно розподілена на проміжку (а, в)
- 6. Рівномірний розподіл Наведемо приклади деяких конкретних величин з рівномірним законом розподілу. При вимірювані багатьох фізичних величин
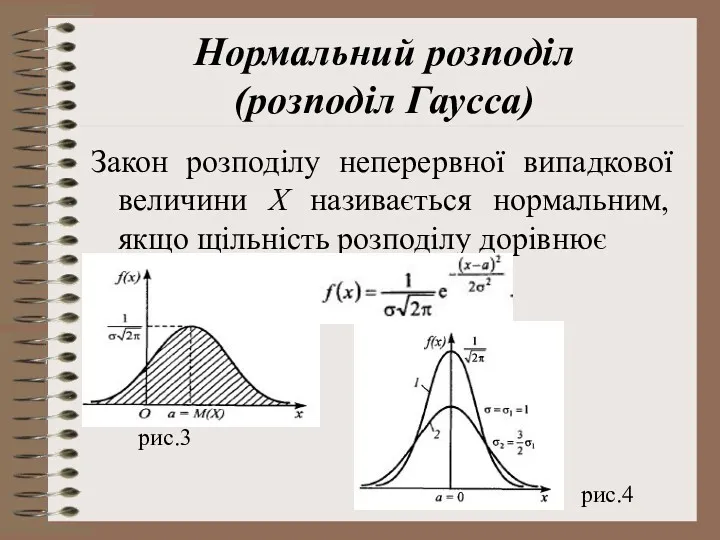
- 7. Нормальний розподіл (розподіл Гаусса) Закон розподілу неперервної випадкової величини Х називається нормальним, якщо щільність розподілу дорівнює
- 8. Нормальний розподіл (розподіл Гаусса) Графік розподілу Гаусса описується симетричною відносно а = М(Х) кривою (рис.3), має
- 9. Нормальний розподіл (розподіл Гаусса) При збільшені квадратичного відхилення ця ордината зменшується. При цьому крива пропорційно звужується
- 10. Нормальний розподіл (розподіл Гаусса) Щільність розподілу в такому випадку дорівнює: Значення функції наведені в таблиці-додатку а
- 11. Функція Лапласа Припустимо, що випадкова величина Х розподілена нормальним законом. Тоді ймовірність того, що Х набуде
- 12. Функція Лапласа Отриманий інтеграл не береться в елементарних функціях, тому для його обчислення вводять функцію яка
- 13. Функція Лапласа Основні властивості функції Лапласа З допомогою функції Лапласа можна знайти ймовірність попадання значень нормально
- 14. Функція Лапласа Згідно з та з урахуванням виконаної раніше підстановки
- 15. Розподіл “х - квадрат” Припустимо, - нормально розподілені незалежні випадкові величини, математичне сподівання кожної з яких
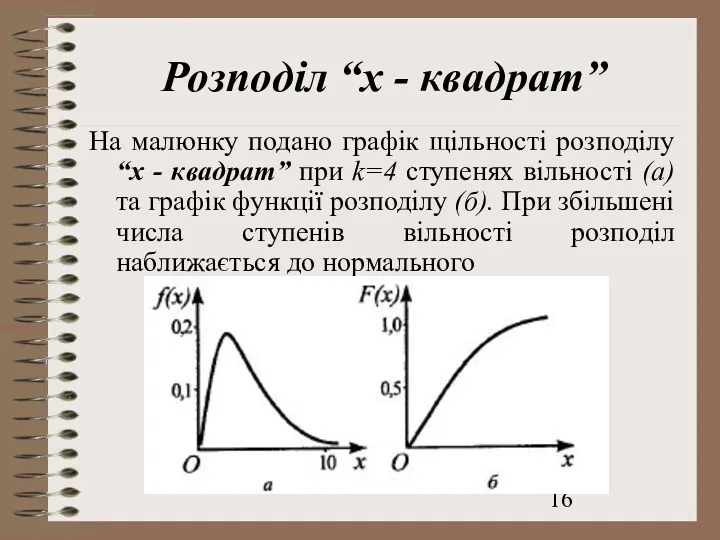
- 16. Розподіл “х - квадрат” На малюнку подано графік щільності розподілу “х - квадрат” при k=4 ступенях
- 17. Розподіл Стьюдента Припустимо що Z – нормально розподілена нормована випадкова величина a V – незалежна від
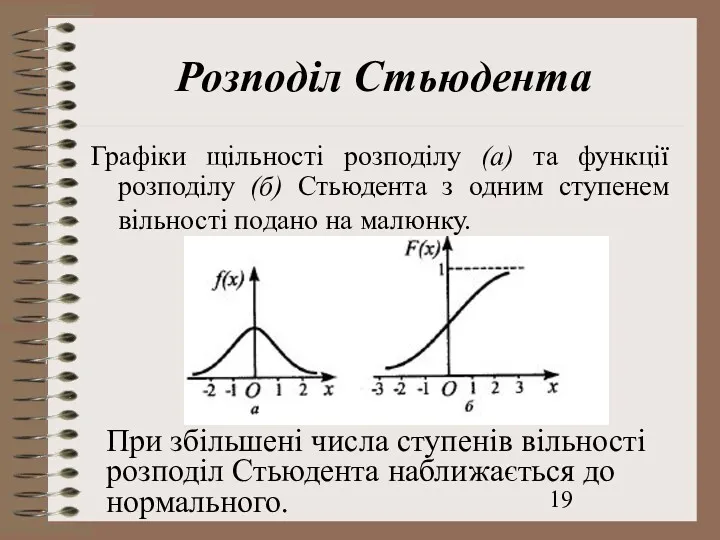
- 18. Розподіл Стьюдента Розподіл Стьюдента повністю визначається числом ступенів вільності і є парною функцією. Щільність ймовірності розподілу
- 19. Розподіл Стьюдента Графіки щільності розподілу (а) та функції розподілу (б) Стьюдента з одним ступенем вільності подано
- 21. Скачать презентацию















 Differential calculus of the function of one variable
Differential calculus of the function of one variable презентации по математике
презентации по математике Жизнь с точки зрения ученого-вероятностника
Жизнь с точки зрения ученого-вероятностника Презентация к уроку математика Уравнение ФГОС
Презентация к уроку математика Уравнение ФГОС Алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины
Алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины Единицы массы
Единицы массы Средняя линия треугольника
Средняя линия треугольника Формулы сокращенного умножения
Формулы сокращенного умножения Числовые ряды
Числовые ряды Способы сложения
Способы сложения Олимпиада по математике для 4класса
Олимпиада по математике для 4класса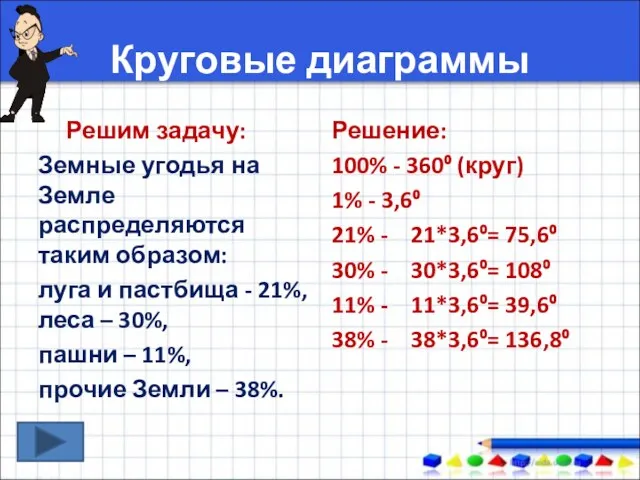 Круговые диаграммы
Круговые диаграммы Математика. 1 класс. Урок 32. Числа 1-5 - Презентация
Математика. 1 класс. Урок 32. Числа 1-5 - Презентация Кто хочет стать отличником? 5 класс
Кто хочет стать отличником? 5 класс Математическое моделирование. Движение по градиенту
Математическое моделирование. Движение по градиенту Теорема Пифагора
Теорема Пифагора Цифры и числа в мире русского языка, биологии и математики
Цифры и числа в мире русского языка, биологии и математики Простые дроби. Повторение
Простые дроби. Повторение Урок по математике 3 класс Единицы измерения массы
Урок по математике 3 класс Единицы измерения массы Составляем и решаем задачи
Составляем и решаем задачи Правильная треугольная пирамида. Решение задач по готовым чертежам
Правильная треугольная пирамида. Решение задач по готовым чертежам Числа, кратные 9
Числа, кратные 9 Сфера. Уравнение сферы
Сфера. Уравнение сферы Уравнения. Закрепление.
Уравнения. Закрепление. Дискриминант квадратных уравнений
Дискриминант квадратных уравнений Случайные события. Вероятность случайного события
Случайные события. Вероятность случайного события Презентация к уроку Вычитание числа. Цифра 8.
Презентация к уроку Вычитание числа. Цифра 8. Математический диктант
Математический диктант