Содержание
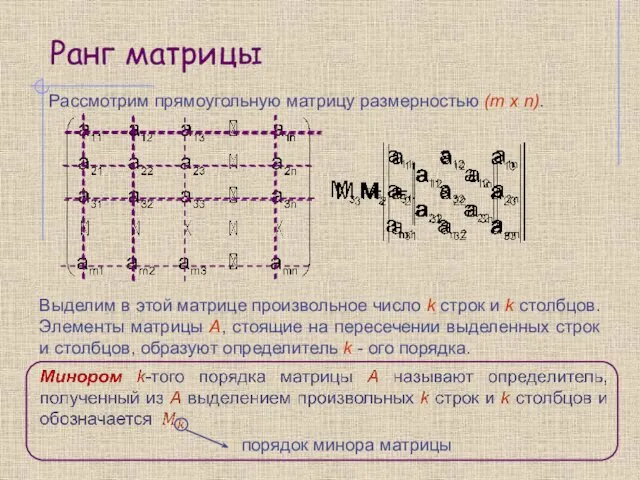
- 2. Ранг матрицы Рассмотрим прямоугольную матрицу размерностью (m x n). Выделим в этой матрице произвольное число k
- 3. Таких миноров матрицы А размера (m x n) можно составить штук, где - число сочетаний из
- 4. Ранг матрицы Матрица А имеет 4 минора 3 - его порядка, например: 18 миноров 2 -
- 5. Свойства ранга матрицы При транспонировании матрицы её ранг не меняется. Если вычеркнуть из матрицы нулевую строку(столбец),
- 6. Методы вычисления ранга матрицы Метод элементарных преобразований (метод Гаусса). Метод окаймляющих миноров. Минор порядка (k+1), который
- 7. Пример: Вычислить ранг матрицы: Решение: Выберем минор второго порядка, находящийся в верхнем левом углу, Вывод: минор
- 9. Все миноры третьего порядка, окаймляющие минор второго порядка, равны нулю. А это значит, что rang A=2.
- 10. Строки (столбцы) S1, S2, … , Sk называют линейно зависимыми, если существуют числа α1, α2, …
- 11. Лемма (о линейной зависимости). Строки (столбцы) S1, S2, … , Sk линейно зависимы тогда и только
- 12. Линейным уравнением называется выражение вида – числа. – коэффициенты уравнения b – свободный член Если ,
- 13. Системой m линейных уравнений с n неизвестными,называется система вида Тогда система принимает вид: AX = B
- 14. Т.е.система в матричном виде примет вид : Если закрепить раз и навсегда нумерацию неизвестных, то можно
- 15. Упорядоченный набор чисел c1, c2, …, cn называется решением системы (*), если он обращает в тождество
- 16. Решить СЛАУ – значит решить две задачи: выяснить, имеет ли СЛАУ решения; найти все решения, если
- 17. Исследование систем линейных уравнений Теорема Кронекера - Капелли. Для того, чтобы система линейных алгебраических уравнений была
- 18. Метод Гаусса решения систем линейных уравнений Следующие действия над расширенной матрицей системы называются элементарными преобразованиями. Умножение
- 19. Метод Гаусса решения систем линейных уравнений Запишем расширенную матрицу системы К первой строке прибавим вторую строку,
- 20. Метод Гаусса решения систем линейных уравнений К третьей строке прибавим вторую строку, умноженную на 4 Вторую
- 21. Исследование систем линейных уравнений
- 22. Исследование систем линейных уравнений система совместна - число неизвестных система неопределенна - число свободных переменных Пусть
- 24. Скачать презентацию





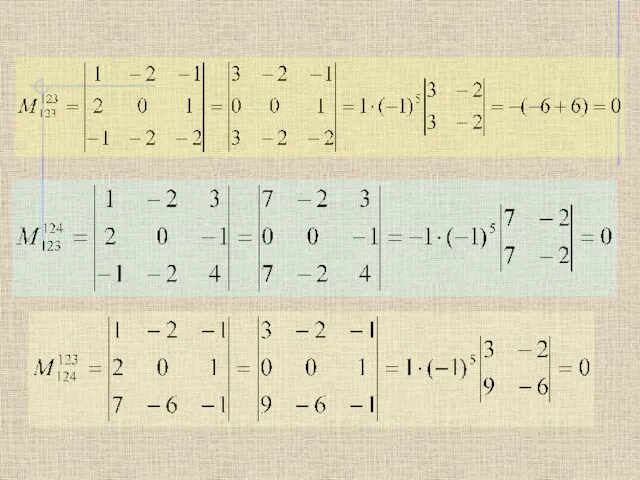














 Многомерная линейная регрессия
Многомерная линейная регрессия Урок математики по теме Свойства сложения, 2 класс
Урок математики по теме Свойства сложения, 2 класс Тройные интегралы
Тройные интегралы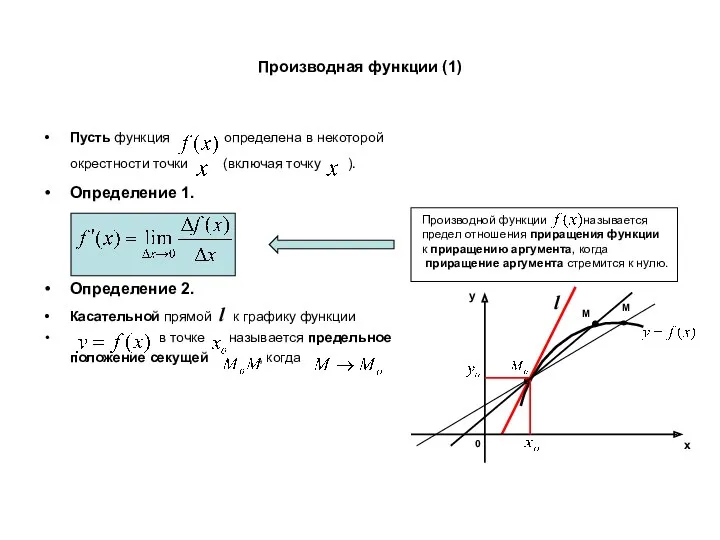 Производная функции
Производная функции Правило решения квадратных уравнений. Историческая справка
Правило решения квадратных уравнений. Историческая справка Отношения эквивалентности и порядка
Отношения эквивалентности и порядка Применение ленты Мёбиуса
Применение ленты Мёбиуса Проект по математике в 4 классе Мир в движении
Проект по математике в 4 классе Мир в движении Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления
Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления Давайте, посчитаем!
Давайте, посчитаем! Логикалық операциялар (дизъюнкция, конъюнкция, инверсия)
Логикалық операциялар (дизъюнкция, конъюнкция, инверсия) Методы оптимизации
Методы оптимизации Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Электронный тренажёр по математике.
Электронный тренажёр по математике. Векторы. Сложение векторов
Векторы. Сложение векторов Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей проверка деления с остатком
проверка деления с остатком Параллельные прямые
Параллельные прямые Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира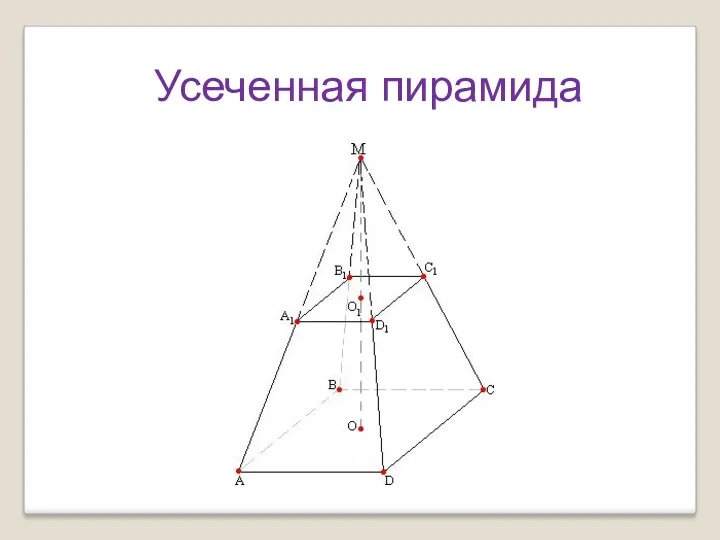 Усеченная пирамида
Усеченная пирамида Система линейных алгебраических уравнений (СЛАУ)
Система линейных алгебраических уравнений (СЛАУ) Деление дробей
Деление дробей Многогранники. Выпуклые и невыпуклые многогранники
Многогранники. Выпуклые и невыпуклые многогранники Принципы симметрии
Принципы симметрии Теория вероятностей. Статистические методы обработки информации
Теория вероятностей. Статистические методы обработки информации Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр
Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр Решение уравнений. 6 класс
Решение уравнений. 6 класс Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций