Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Семинар 36) презентация
Содержание
- 2. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Однородное уравнение. Линейное уравнение 2-го порядка с постоянными
- 3. Неоднородное уравнение Общее решение линейного неоднородного дифференциального уравнения можно записать в виде суммы , где -
- 4. Если же то полагают где - многочлены степени N=max{n,m}, r – кратность корней (для уравнений 2-го
- 5. Пусть известна фундаментальная система решений . Тогда общее решение неоднородного уравнения следует искать в виде: где
- 6. Примеры с решениями. Найти общее решение уравнения y’’-5y’+6y=0 Решение. Составим характеристическое уравнение его корни Следовательно, -
- 7. Частное решение следует искать в виде: (в данном случае так как корня 0 у характеристического уравнения
- 8. Решить уравнение Решение. Характеристическое уравнение имеет корни а поэтому общее решение однородного уравнения: Пользуясь принципом наложения,
- 9. Решая систему уравнений: Следовательно, общее решение исходного уравнения: Итак,
- 10. Примеры для самостоятельного решения Найти общие решения уравнения: Найти решения уравнений, удовлетворяющие заданным начальным или краевым
- 12. Скачать презентацию









 Многомерная линейная регрессия
Многомерная линейная регрессия Урок математики по теме Свойства сложения, 2 класс
Урок математики по теме Свойства сложения, 2 класс Тройные интегралы
Тройные интегралы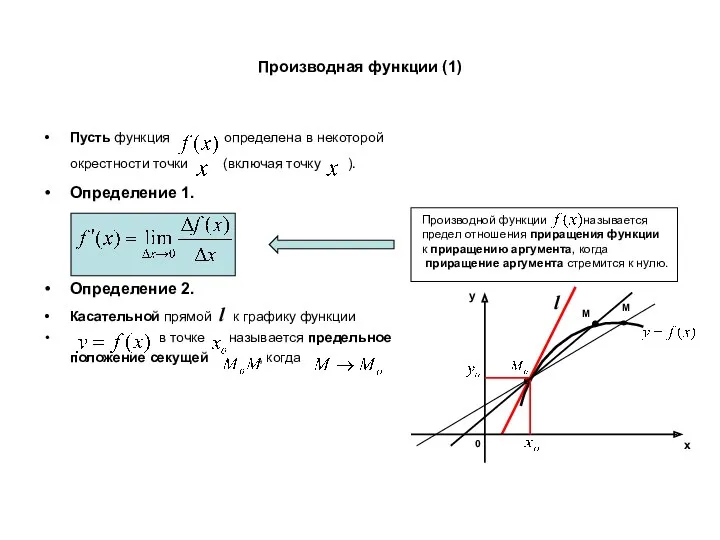 Производная функции
Производная функции Правило решения квадратных уравнений. Историческая справка
Правило решения квадратных уравнений. Историческая справка Отношения эквивалентности и порядка
Отношения эквивалентности и порядка Применение ленты Мёбиуса
Применение ленты Мёбиуса Проект по математике в 4 классе Мир в движении
Проект по математике в 4 классе Мир в движении Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления
Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления Давайте, посчитаем!
Давайте, посчитаем! Логикалық операциялар (дизъюнкция, конъюнкция, инверсия)
Логикалық операциялар (дизъюнкция, конъюнкция, инверсия) Методы оптимизации
Методы оптимизации Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Электронный тренажёр по математике.
Электронный тренажёр по математике. Векторы. Сложение векторов
Векторы. Сложение векторов Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей проверка деления с остатком
проверка деления с остатком Параллельные прямые
Параллельные прямые Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира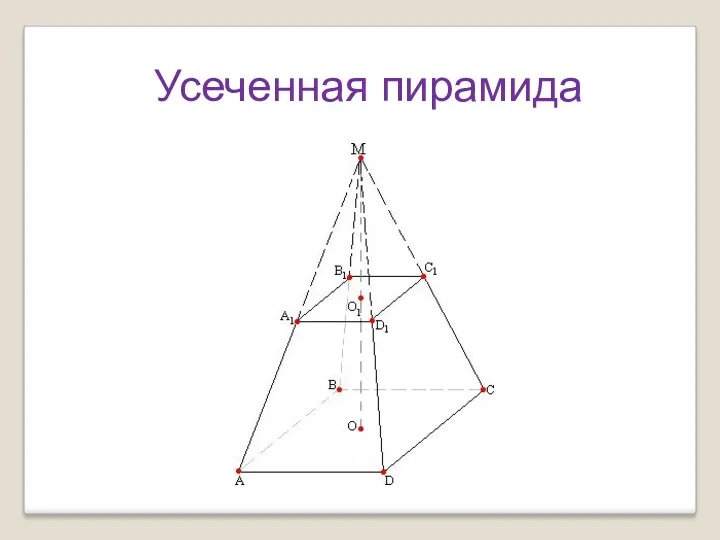 Усеченная пирамида
Усеченная пирамида Система линейных алгебраических уравнений (СЛАУ)
Система линейных алгебраических уравнений (СЛАУ) Деление дробей
Деление дробей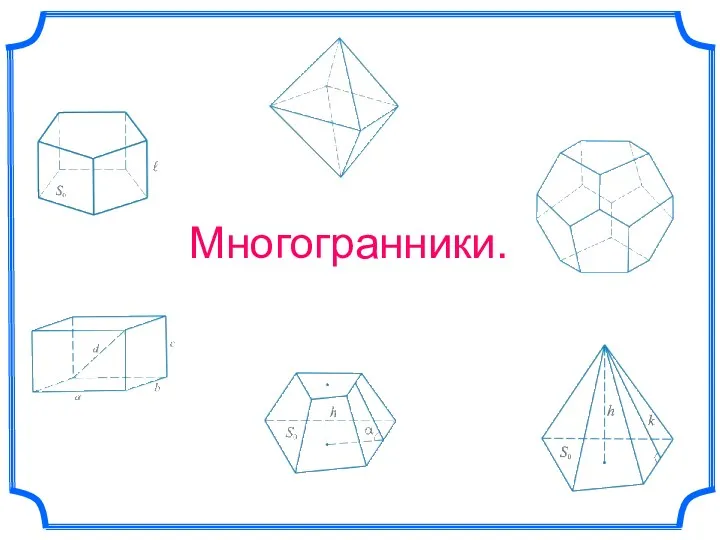 Многогранники. Выпуклые и невыпуклые многогранники
Многогранники. Выпуклые и невыпуклые многогранники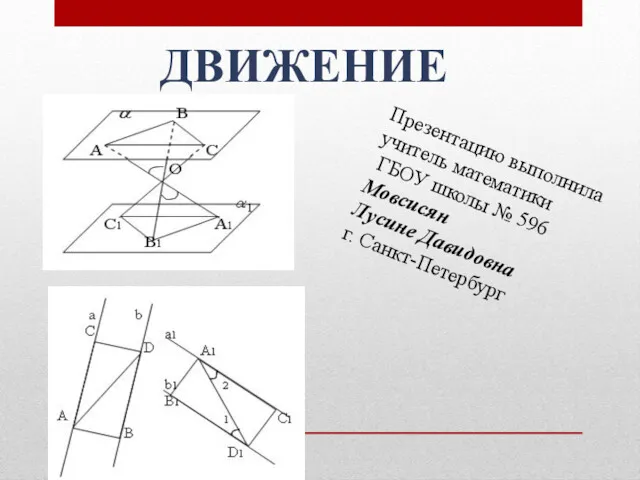 Принципы симметрии
Принципы симметрии Теория вероятностей. Статистические методы обработки информации
Теория вероятностей. Статистические методы обработки информации Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр
Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр Решение уравнений. 6 класс
Решение уравнений. 6 класс Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций