Содержание
- 2. Уравнение вида называется линейным ДУ с постоянными коэффициентами 9
- 3. Где у – искомая функция, p, g – постоянные величины. Если f(х)=0, то уравнение называется линейным
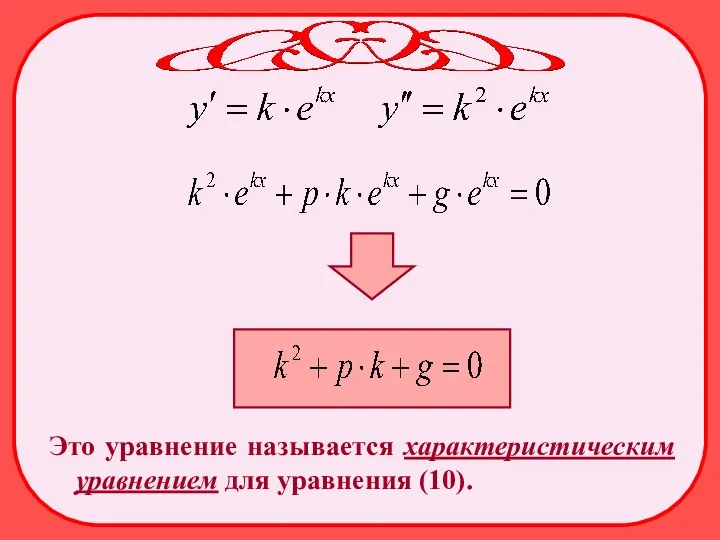
- 4. Рассмотрим сначала однородное уравнение: Будем искать решение этого уравнения в виде Где k - некоторое число.
- 5. Это уравнение называется характеристическим уравнением для уравнения (10).
- 6. Вид решения линейного однородного ДУ (10) существенно зависит от того, какие корни имеет его характеристическое уравнение.
- 7. ТЕОРЕМА. Если корни характеристического уравнения вещественные и разные то общее решение однородного уравнения (9) имеет вид:
- 8. Если корни характеристического уравнения вещественные и равные то общее решение однородного уравнения (10) имеет вид:
- 9. Если характеристическое уравнение не имеет вещественных корней, то общее решение однородного уравнения (10) имеет вид: где
- 10. ПРИМЕРЫ. Решить дифференциальное уравнение: 1
- 11. Решение: Корни вещественные и разные, поэтому общее решение будет иметь вид:
- 12. Решить дифференциальное уравнение: 2
- 13. Решение: Корни вещественные и одинаковые, поэтому общее решение будет иметь вид:
- 14. Решить дифференциальное уравнение: 3
- 15. Решение: Корни комплексные, поэтому общее решение будет иметь вид:
- 16. Теперь рассмотрим решение неоднородного ЛДУ с постоянными коэффициентами (9). Общее решение неоднородного ЛДУ с постоянными коэффициентами
- 17. ПРИМЕР. Решить дифференциальное уравнение:
- 18. Решение: Сначала находим общее решение однородного уравнения:
- 19. Корни вещественные и разные, поэтому общее решение будет иметь вид: Теперь находим частное решение неоднородного уравнения
- 20. Пусть Тогда Подставляем в уравнение:
- 21. Получаем:
- 22. Вычитаем из второго уравнения первое: Теперь подставляем в первое уравнение:
- 23. Интегрируем эти выражения: Частное решение неоднородного уравнения имеет вид: Общее решение будет:
- 24. Частное решение неоднородного уравнения можно найти, используя следующую схему:
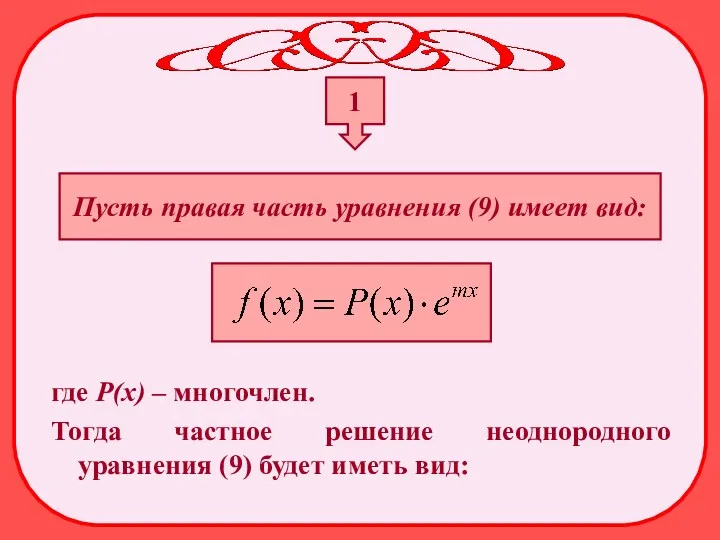
- 25. 1 Пусть правая часть уравнения (9) имеет вид: где Р(х) – многочлен. Тогда частное решение неоднородного
- 26. где Q(х) – многочлен той же степени, что и Р(х). Причем, если m не является корнем
- 27. ПРИМЕР. Решить дифференциальное уравнение:
- 28. Решение: Корни вещественные и одинаковые, поэтому общее решение однородного уравнения будет иметь вид: Сначала решаем однородное
- 29. Теперь решаем неоднородное уравнение. Правая часть представляет собой рассмотренный случай: m – не является корнем характеристического
- 30. Находим производные и подставляем в исходное уравнение: Частное решение неоднородного уравнения имеет вид:
- 31. Общее решение неоднородного уравнения запишем как сумму общего решения однородного уравнения и частного решения неоднородного уравнения:
- 32. 2 Пусть правая часть уравнения (9) имеет вид:
- 33. Если числа не являются корнями характеристического уравнения, то частное решение неоднородного уравнения (9) будет иметь вид:
- 34. ПРИМЕР. Решить дифференциальное уравнение:
- 35. Решение: Сначала решаем однородное уравнение:
- 36. Корни комплексные, поэтому общее решение будет иметь вид: Теперь решаем неоднородное уравнение. Правая часть представляет собой
- 37. Находим производные и подставляем в исходное уравнение:
- 38. Частное решение неоднородного уравнения имеет вид: Общее решение неоднородного уравнения запишем как сумму общего решения однородного
- 39. 3 Пусть правая часть уравнения (9) имеет вид: где Р1(х) и Р2(х) – многочлены.
- 40. Если числа не являются корнями характеристического уравнения, то частное решение неоднородного уравнения (9) будет иметь вид:
- 42. Скачать презентацию





































 Свойства степени с натуральным показателем. Открытый урок. 7 класс
Свойства степени с натуральным показателем. Открытый урок. 7 класс Теорема Пифагора
Теорема Пифагора игра-тренажер
игра-тренажер Площадь фигур
Площадь фигур Письменное деление многозначных чисел на трехзначное число
Письменное деление многозначных чисел на трехзначное число Проверка статистической гипотезы
Проверка статистической гипотезы Система молниезащиты зданий и сооружений обычного типа
Система молниезащиты зданий и сооружений обычного типа Математическая регата. Викторина для семиклассников
Математическая регата. Викторина для семиклассников Вычитание суммы из числа
Вычитание суммы из числа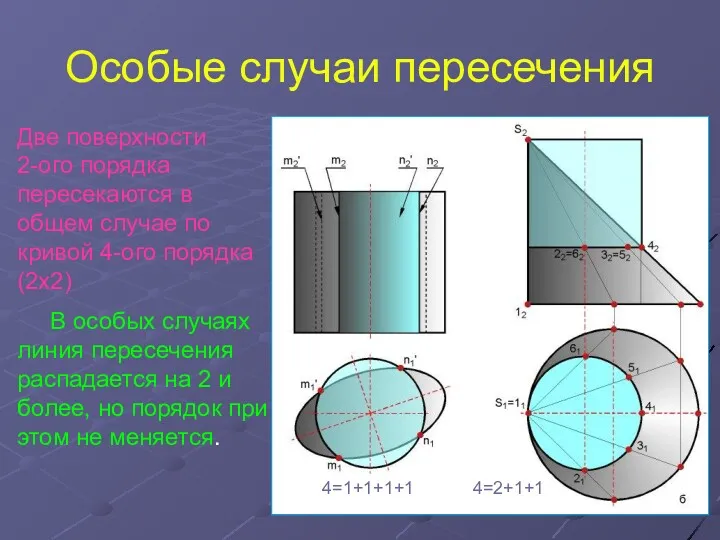 Особые случаи пересечения. Пересечение соосных поверхностей вращения. Теорема Монжа
Особые случаи пересечения. Пересечение соосных поверхностей вращения. Теорема Монжа Нумерация чисел первого десятка
Нумерация чисел первого десятка Луч - линия, у которой есть начало и нет конца
Луч - линия, у которой есть начало и нет конца Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел Числовые ряды. Общие определения и свойства. Сходимость рядов. Признаки сходимости. (Семинар 25)
Числовые ряды. Общие определения и свойства. Сходимость рядов. Признаки сходимости. (Семинар 25) Модуль числа
Модуль числа Числовые ряды
Числовые ряды Наглядная геометрия на уроках математики в 5-6 классах
Наглядная геометрия на уроках математики в 5-6 классах Презентация Задачи осени. Диск
Презентация Задачи осени. Диск Презентация по математике в 1 классе по темеКомпоненты сложения
Презентация по математике в 1 классе по темеКомпоненты сложения Решение задач ЕГЭ с применением графиков функций, уравнений, неравенств
Решение задач ЕГЭ с применением графиков функций, уравнений, неравенств Задачі на збільшення на декілька одиниць. Порівняння виразу і числа. Урок №54. Математика
Задачі на збільшення на декілька одиниць. Порівняння виразу і числа. Урок №54. Математика Нахождение числа по его дроби. Демонстрационный материал. 6 класс
Нахождение числа по его дроби. Демонстрационный материал. 6 класс Презентация к уроку по математике Решение задач на уменьшение числа в несколько раз 3 класс
Презентация к уроку по математике Решение задач на уменьшение числа в несколько раз 3 класс Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Действительные числа
Действительные числа Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Стереометрия аксиомалары
Стереометрия аксиомалары Методика формирования элементарных математических представлений как научная область
Методика формирования элементарных математических представлений как научная область