Линейные операции. Проекция вектора на ось. Скалярное произведение векторов. Базис векторов. Тема 5 презентация
Содержание
- 2. Основные определения векторной алгебры Вектором называется направленный отрезок. Длиной вектора называется длина задающего его направленного отрезка.
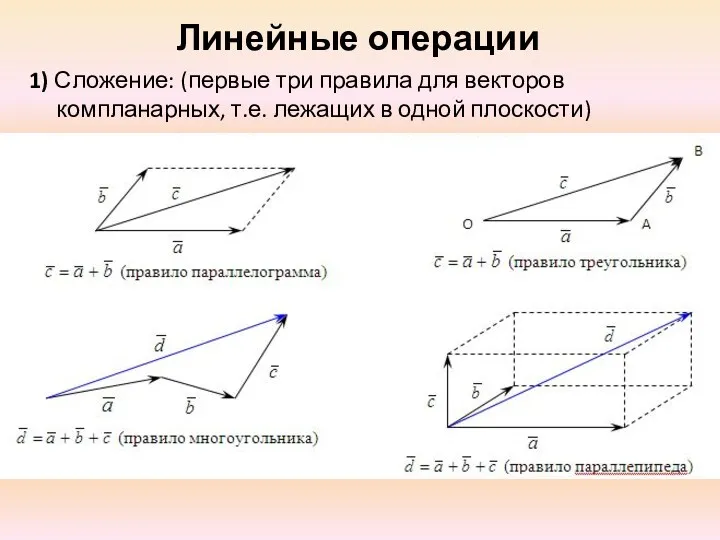
- 3. Линейные операции 1) Сложение: (первые три правила для векторов компланарных, т.е. лежащих в одной плоскости)
- 4. Линейные операции 2) Вычитание: 3) Умножение на число:
- 5. Свойства линейных операций
- 6. Проекция вектора на ось
- 7. Свойства проекций:
- 8. Скалярное произведение векторов Если скалярное произведение векторов равно нулю, то вектора называют ортогональными.
- 9. Скалярное произведение в координатах Применение скалярного произведения
- 10. Базис векторов
- 11. Чаще всего пользуются прямоугольным базисом
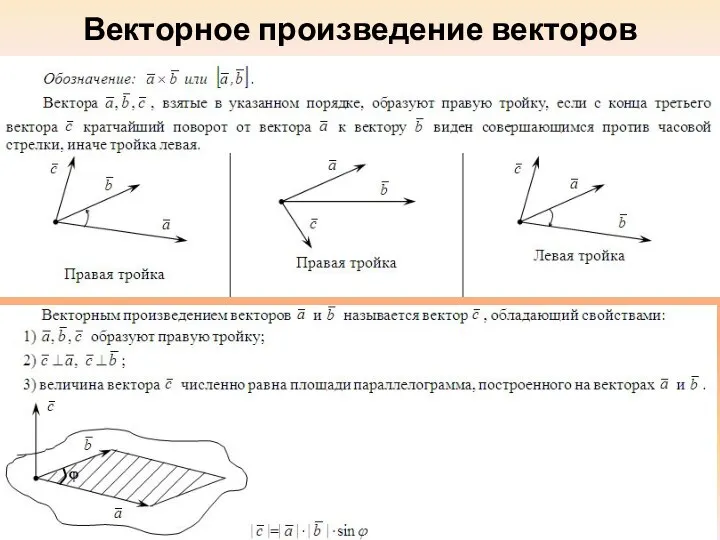
- 14. Векторное произведение векторов
- 17. Смешанное произведение векторов
- 19. РЕШЕНИЕ ЗАДАЧ Примеры вычисления длины вектора Пример. Найти длину вектора a = {2; 4; 4}. Решение:
- 20. Примеры вычисления проекции вектора Пример. Найти проекцию вектора a = {1; 4; 0} на вектор b
- 21. Вычисление угла между векторами Пример. Найти угол между векторами a = {3; 4; 0} и b
- 22. Пример. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c
- 23. Коллинеарность векторов Пример. найти значение параметра n при котором вектора a = {3; 2} и b
- 24. Ортогональность векторов Пример . Проверить являются ли вектора a = {3; -1} и b = {7;
- 25. Вычисление координат Пример. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1). Решение: AB
- 26. Смешанное произведение векторов Пример. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1;
- 27. Базис векторов
- 32. Скачать презентацию



























 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Эконометрика. Обобщенный метод наименьших квадратов
Эконометрика. Обобщенный метод наименьших квадратов Треугольник. Четырехугольник. Окружность. Путешествие в геометрию
Треугольник. Четырехугольник. Окружность. Путешествие в геометрию Применение производной и первообразной показательной и логарифмической функции
Применение производной и первообразной показательной и логарифмической функции Неравенства
Неравенства Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке Величины 1 класс
Величины 1 класс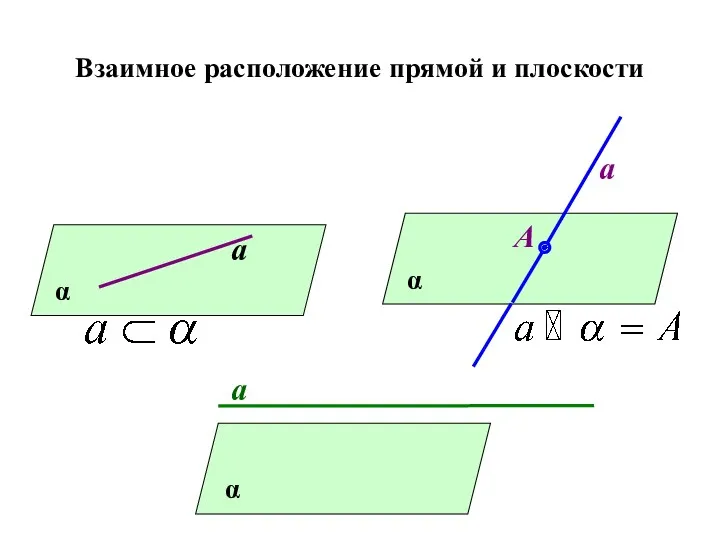 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости 20231001_mnogougolniki
20231001_mnogougolniki Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени
Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени Презентация Путешествие в страну дробей
Презентация Путешествие в страну дробей Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Как правильно писать цифры
Как правильно писать цифры Элементы теории вероятностей
Элементы теории вероятностей Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Тренировочная работа № 3
Тренировочная работа № 3 Площади. Равновеликие фигуры
Площади. Равновеликие фигуры Представление натуральных чисел на координатном луче
Представление натуральных чисел на координатном луче Скорость, время, расстояние. Математика, 4класс.
Скорость, время, расстояние. Математика, 4класс. ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов
ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Геометрические фигуры
Геометрические фигуры Математика. 1 класс. Урок 4. Признаки предметов
Математика. 1 класс. Урок 4. Признаки предметов Задача по финансовой математике
Задача по финансовой математике Правильный додекаэдр
Правильный додекаэдр Геометрические фигуры (презентация для подготовки)
Геометрические фигуры (презентация для подготовки) Вклад математиков в победу Великой Отечественной Войне
Вклад математиков в победу Великой Отечественной Войне Конспект урока математики (+ презентация). 4 класс
Конспект урока математики (+ презентация). 4 класс