Содержание
- 2. Около 1800 года до н.э. В вавилонских табличках объясняется, как решать квадратные уравнения
- 3. Около 500 года до н.э. Пифагор Самосский создает свою знаменитую теорему о прямоугольном треугольнике: квадрат гипотенузы
- 4. VII век н.э. Индийский математик Брахмагупта пишет труд, который считается самым ранним текстом, где ноль осмысливается
- 5. 1792 год 15-летний Карл Фридрих Гаусс находит плотность распределения простых чисел
- 6. 1637 год Пьер Ферма, отец-основатель числовой теории, разрабатывает свою «Последнюю теорему», которая гласит: «Если целое число
- 7. 2002 год Российский математик Григорий Перельман доказывает гипотезу Пуанкаре, предполагающую математическую возможность существования определенной формы у
- 8. 2011 год. 11а обнаруживает в переводах работ Архимеда неполное доказательство одной из его лемм, и сегодня
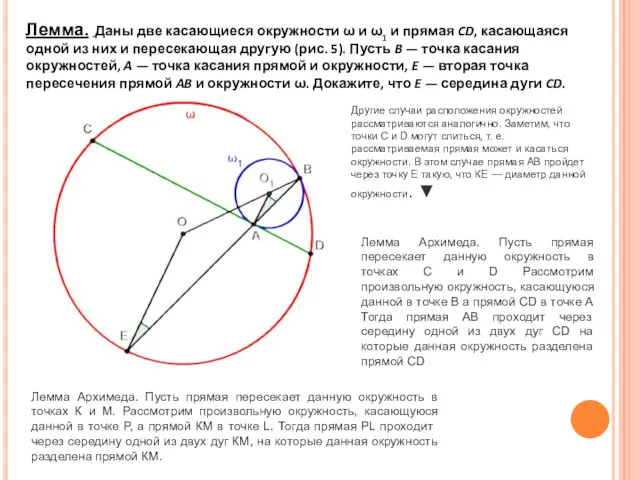
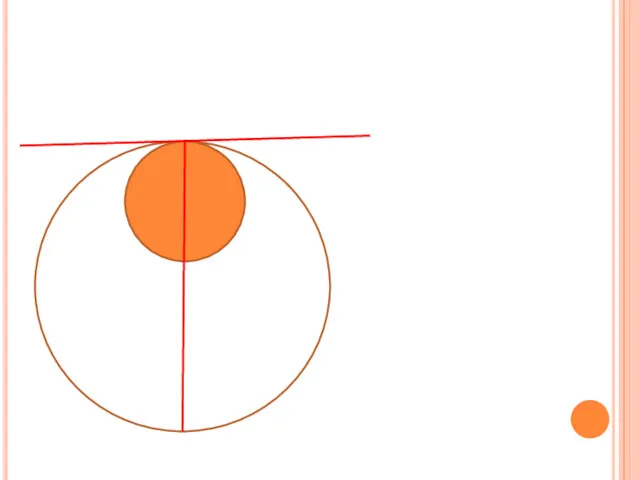
- 11. Лемма. Даны две касающиеся окружности ω и ω1 и прямая CD, касающаяся одной из них и
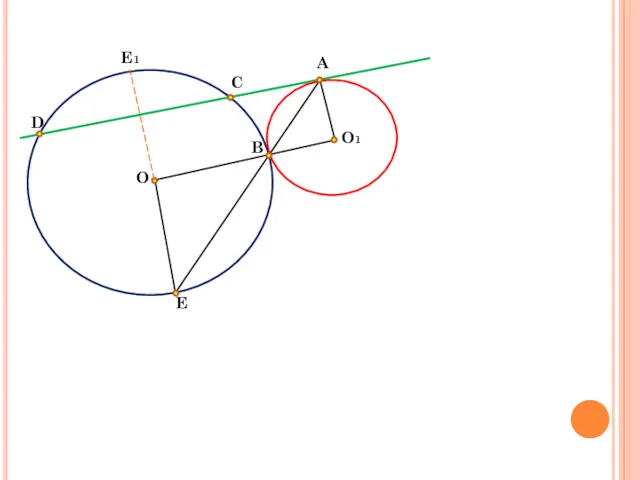
- 12. A B C D O E O1 E1
- 14. Многовариантные задачи
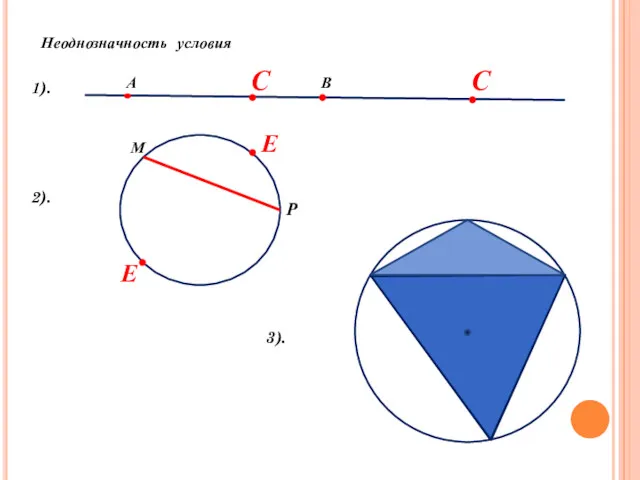
- 15. Неоднозначность условия А В С С 1). 2). М Р Е Е 3).
- 16. Задача .Длина окружности, описанной около равнобедренного треугольника, равна 20 . Найдите площадь этого треугольника, если его
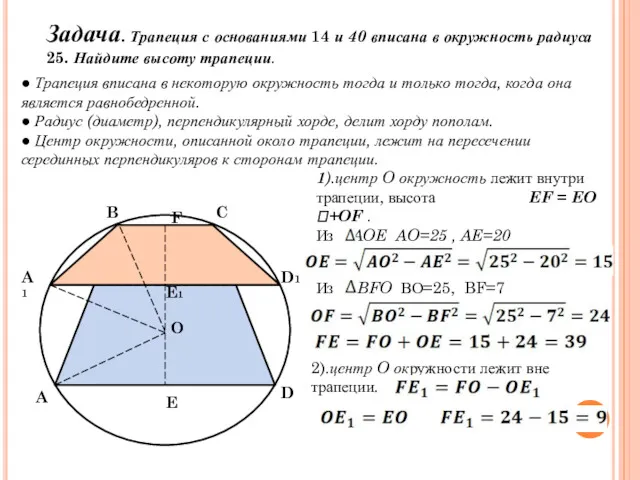
- 17. Задача. Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции. ●
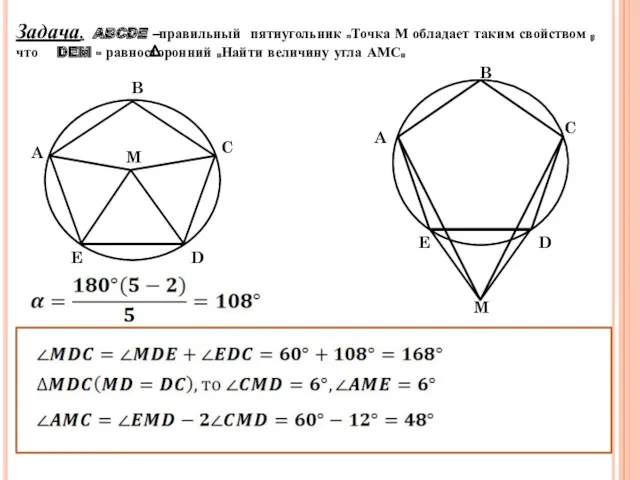
- 18. Задача. ABCDE –правильный пятиугольник .Точка М обладает таким свойством , что DEM - равносторонний .Найти величину
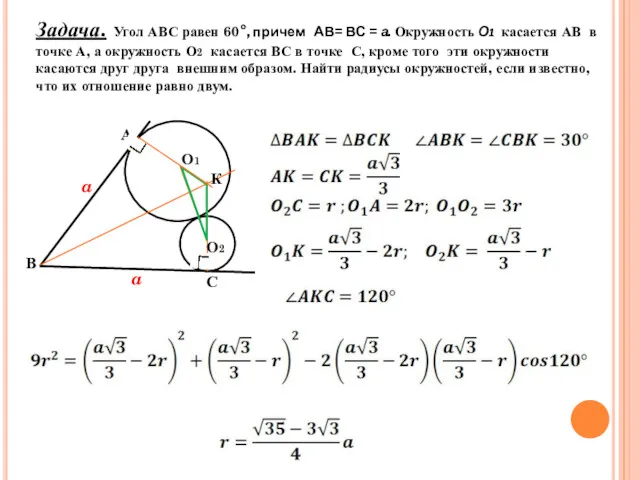
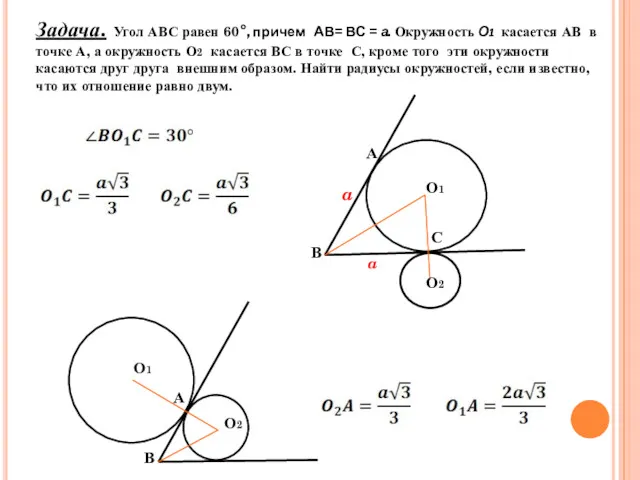
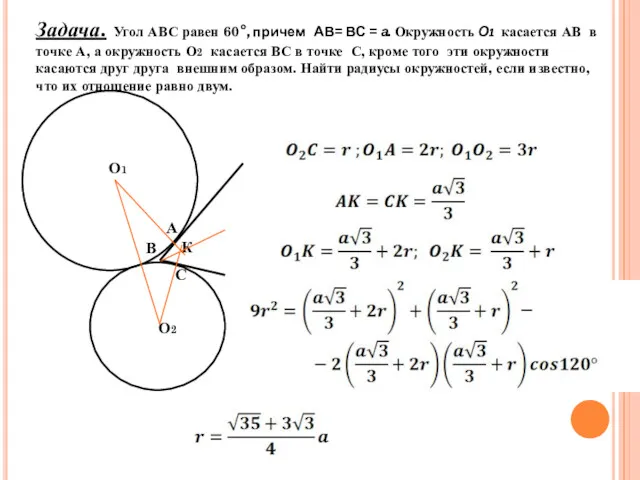
- 19. Задача. Угол АВС равен 60°, причем АВ= ВС = а. Окружность О1 касается АВ в точке
- 20. Задача. Угол АВС равен 60°, причем АВ= ВС = а. Окружность О1 касается АВ в точке
- 21. Задача. Угол АВС равен 60°, причем АВ= ВС = а. Окружность О1 касается АВ в точке
- 22. Задача. Угол АВС равен 60°, причем АВ= ВС = а. Окружность О1 касается АВ в точке
- 23. Oтвет: 1). 2). 3). 4).
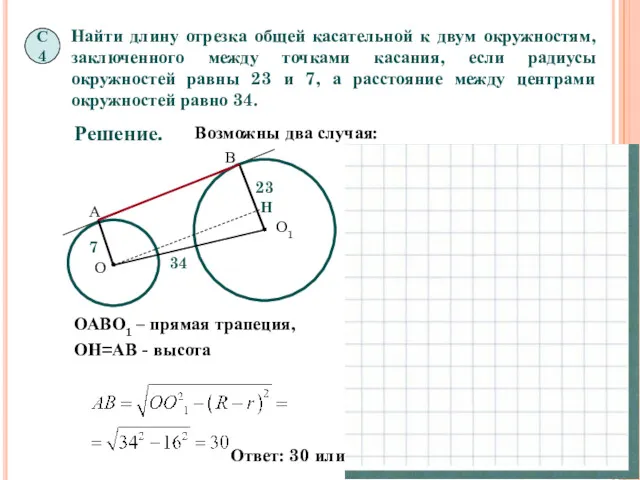
- 24. Найти длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны
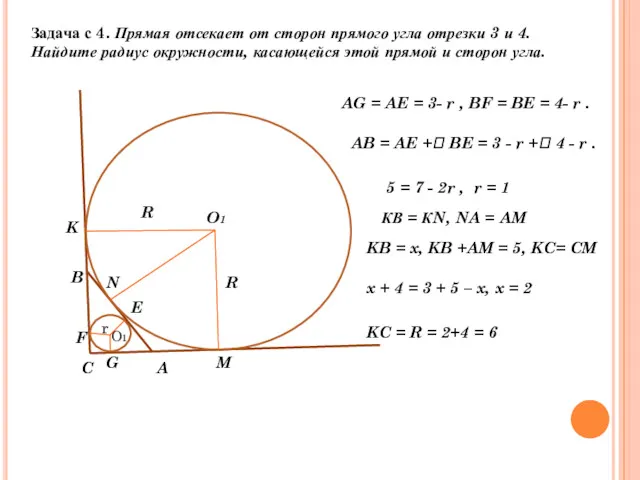
- 25. Задача с 4. Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найдите радиус окружности,
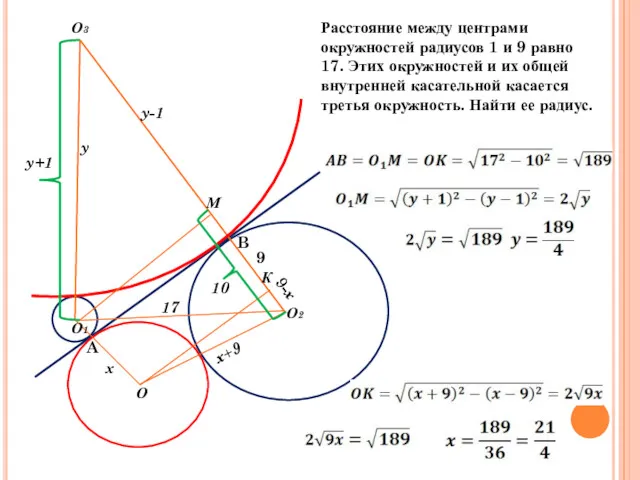
- 26. Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Этих окружностей и их общей внутренней
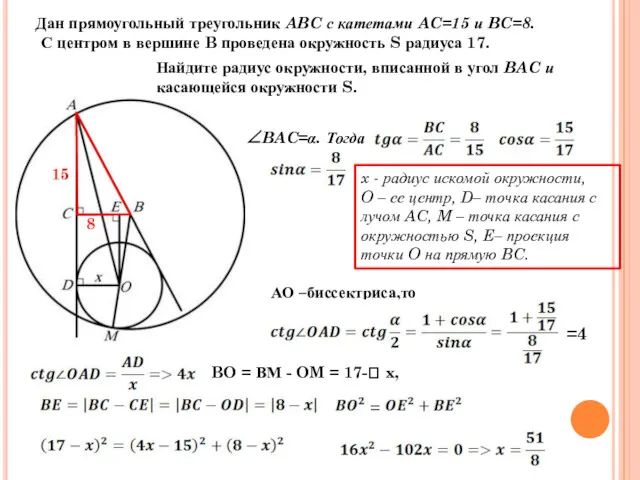
- 27. Дан прямоугольный треугольник ABC с катетами AC=15 и BC=8. С центром в вершине B проведена окружность
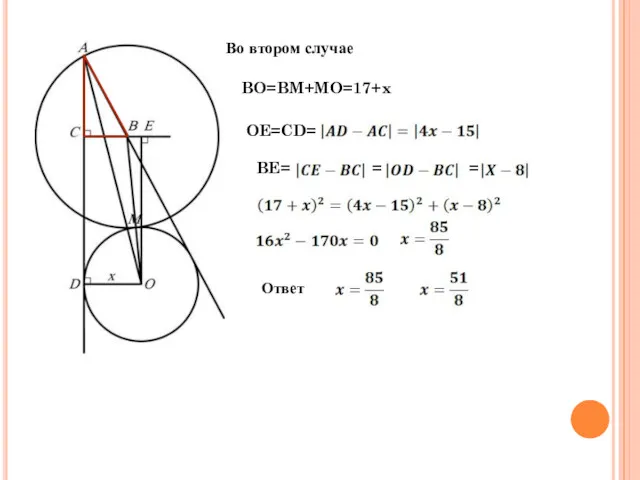
- 28. Во втором случае BO=BM+MO=17+x OE=CD= BE= = = Ответ
- 30. Скачать презентацию













 Координаты вектора
Координаты вектора Нахождение однозначного частного путем подбора
Нахождение однозначного частного путем подбора Матриці та дії над ними
Матриці та дії над ними Дисперсиялық талдау. Крускал-Уоллис критерийі
Дисперсиялық талдау. Крускал-Уоллис критерийі фоны презентаций Диск Диск Диск Диск Диск
фоны презентаций Диск Диск Диск Диск Диск Числа от 1 до 1000. Приём письменного вычитания трёхзначных чисел
Числа от 1 до 1000. Приём письменного вычитания трёхзначных чисел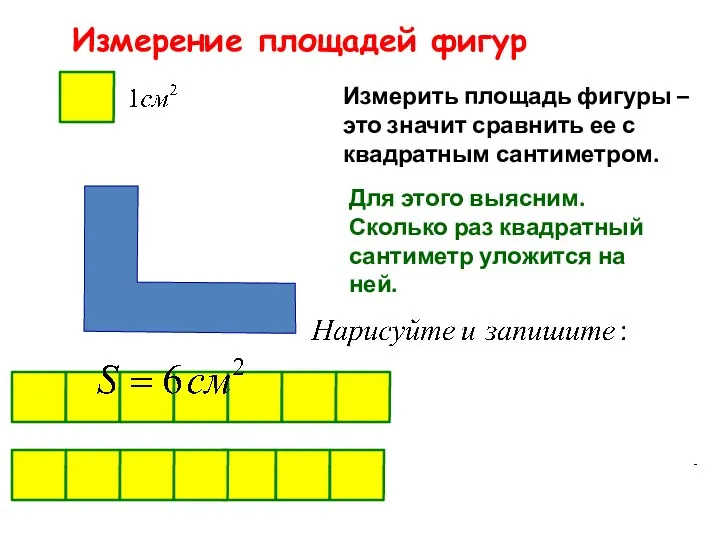 Измерение площадей фигур
Измерение площадей фигур Урок математики в 3 классе по теме: Деление двузначного числа на однозначное
Урок математики в 3 классе по теме: Деление двузначного числа на однозначное Математический тренажер по решению задач на нахождение периметра.
Математический тренажер по решению задач на нахождение периметра. Линейная регрессия
Линейная регрессия Определители
Определители Трапеция. Свойства
Трапеция. Свойства Үлес
Үлес Сыбайлас және вертикаль бұрыштар
Сыбайлас және вертикаль бұрыштар Таблица сложения с переходом через 10
Таблица сложения с переходом через 10 Страна геометрических фигур
Страна геометрических фигур Тела и поверхности вращения. Цилиндр
Тела и поверхности вращения. Цилиндр Найди значение выражений
Найди значение выражений Задание 10: Задачи с прикладным содержанием
Задание 10: Задачи с прикладным содержанием Объем цилиндрического тела. Двойной интеграл. (Лекция 2.1)
Объем цилиндрического тела. Двойной интеграл. (Лекция 2.1) Среднее арифметическое. Деление десятичной дроби на натуральное число. 5 класс
Среднее арифметическое. Деление десятичной дроби на натуральное число. 5 класс Графическое представление статистических данных
Графическое представление статистических данных Координатная плоскость
Координатная плоскость Наибольший общий делитель
Наибольший общий делитель Исчисление высказываний. Элементы теории алгоритмов
Исчисление высказываний. Элементы теории алгоритмов Отношения между множествами
Отношения между множествами Решение текстовых задач. Задачи на движение
Решение текстовых задач. Задачи на движение Функции. Основные характеристики функции. Чётность функции
Функции. Основные характеристики функции. Чётность функции