Содержание
- 2. цель развитие творческих способностей; творческого мышления; расширение общего кругозора учащихся в процессе рассмотрения различных практических задач;
- 3. Что такое софизм? Софизмом называется умышленно ложное умозаключение, которое кажется правильным. Софизм основан на сознательном нарушении
- 4. ВИДЫ МАТЕМАТИЧЕСКИХ СОФИЗМОВ Математический кружок Геометрические софизмы – рассуждения, обосновывающие какую-нибудь нелепость, связанную с геометрическими фигурами
- 5. Экскурсия в историю Термин «софизм» впервые ввел Аристотель Математический кружок Возникновение софизмов связывается с философией софистов,
- 6. Примеры софизмов Математический кружок 9кг = 9000000г 2 х 2 = 5 или 4 = 5
- 7. 9кг = 9.000.000г Математический кружок 1кг = 1000г 3кг = 3000г Возведём правую и левую части
- 8. 2 х 2 = 5 Математический кружок 4 = 5 1 способ 2 способ 3 способ
- 9. Математический кружок 2 Х 2=5 или 4=5 4 : 4 = 5 : 5 4 x
- 10. 4 = 5 Математический кружок 16 – 36 = 25 – 45 Дополним до полного квадрата
- 11. Пусть 4=а, 5=b, тогда найдём среднее арифметическое этих чисел:(а+b)/2=d Умножим обе части равенства на 2: a+b=2d
- 12. Математический кружок Пусть 4 = 5 Из обеих частей равенства вычтем среднее арифметическое чисел 4 и
- 13. Математический кружок 2 = 5 5=12=58 2 : 2 = 5 : 5 2(1 : 1)
- 14. Рассмотрим ∆АВС. На сторонах АВ и ВС ΔАВС, как на диаметрах, построим полуокружности. Эти полуокружности пересекают
- 15. Чем полезны софизмы? Развивают логическое мышление Развивают наблюдательность, вдумчивость, критическое отношение к тому, что изучается Заставляют
- 17. Скачать презентацию














 Представление рациональных чисел в виде десятичной дроби (продолжение)
Представление рациональных чисел в виде десятичной дроби (продолжение) Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20
Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20 Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Арифметическая игра Числовые Домики
Арифметическая игра Числовые Домики Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Смешанные числа. Обыкновенные дроби. Математика. 5 класс
Смешанные числа. Обыкновенные дроби. Математика. 5 класс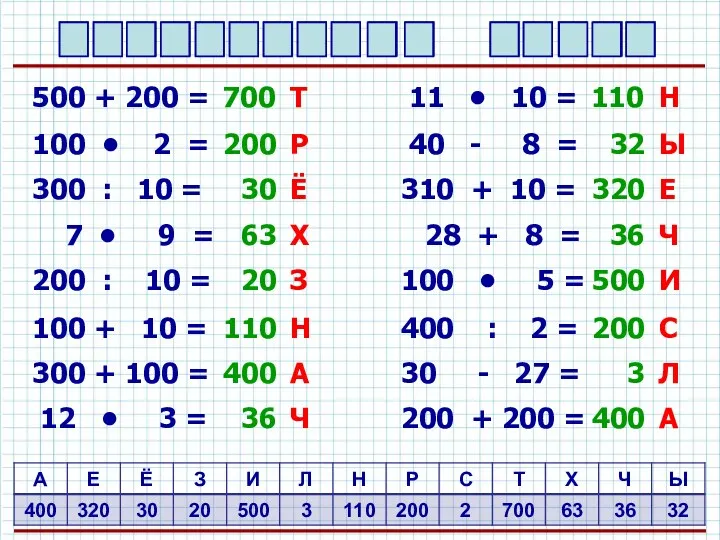 Сложение и вычитание трёхзначных чисел Презентация к уроку математики 3 класс
Сложение и вычитание трёхзначных чисел Презентация к уроку математики 3 класс Деление (математика, 3 класс, УМК Гармония)
Деление (математика, 3 класс, УМК Гармония) Презентация Времена года
Презентация Времена года ЦМР к уроку математики в 1 классе Дециметр - новая единица длины
ЦМР к уроку математики в 1 классе Дециметр - новая единица длины Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2 Множества и матрицы
Множества и матрицы Презентация Веселая математика с Винни-Пухом
Презентация Веселая математика с Винни-Пухом Площадь треугольника
Площадь треугольника Двузначные числа
Двузначные числа Решение задач с помощью кругов Эйлера
Решение задач с помощью кругов Эйлера Десятичные дроби и действия над ними
Десятичные дроби и действия над ними Окружность. Касательная к окружности
Окружность. Касательная к окружности Распределительное свойство умножения
Распределительное свойство умножения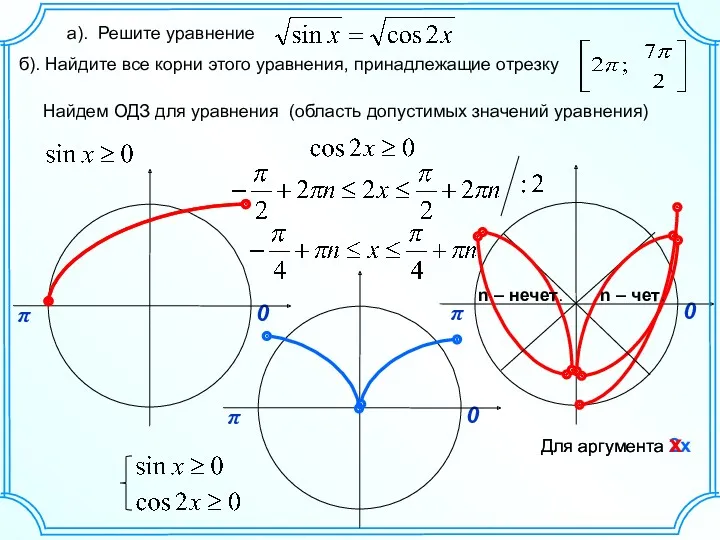 Решение тригонометрического уравнения (С 1, 26)
Решение тригонометрического уравнения (С 1, 26) Методические разработки учителя математики
Методические разработки учителя математики Скорость. Время. Расстояние
Скорость. Время. Расстояние Презентация к уроку математики в 4 классе.
Презентация к уроку математики в 4 классе. презентация к уроку математики Решение задач на движение
презентация к уроку математики Решение задач на движение Дисперсия дискретной случайной величины
Дисперсия дискретной случайной величины Экономические задачи в заданиях ЕГЭ по математике
Экономические задачи в заданиях ЕГЭ по математике Приёмы устных вычислений вида 450+30; 620-200
Приёмы устных вычислений вида 450+30; 620-200 Сложение и вычитание десятичных дробей. Урок 111
Сложение и вычитание десятичных дробей. Урок 111