Содержание
- 2. Место и содержание курса 1. Логика 2. Математика а) линейная алгебра б) математический анализ в) теория
- 4. Основная литература 1. Высшая математика для экономических специальностей. Учебник и Практикум (части I и II) /
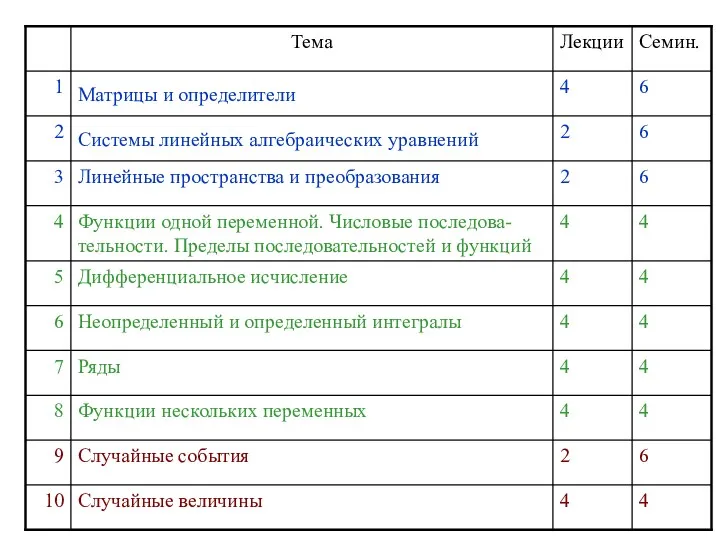
- 5. Тема 1. Матрицы и определители Лекция 1
- 6. Матрицы. Определение и виды. Опр. 1. Матрицей размера (m на n) называется прямоугольная таблица чисел, содержащая
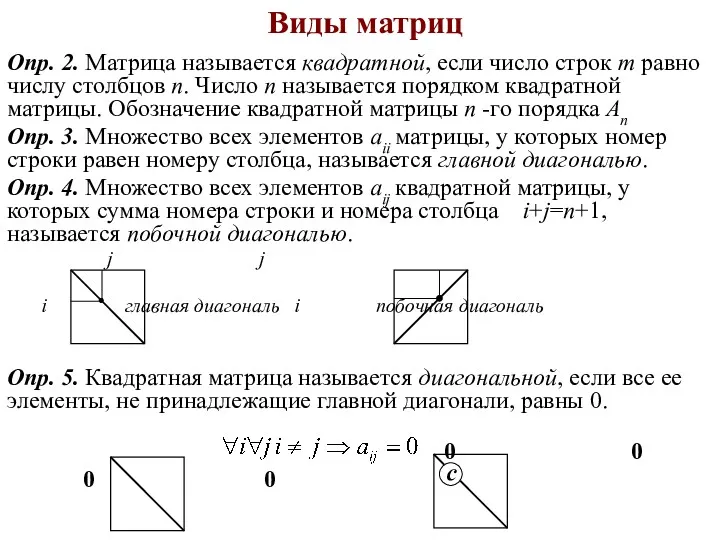
- 7. Виды матриц Опр. 2. Матрица называется квадратной, если число строк m равно числу столбцов n. Число
- 8. Виды матриц Опр. 6. Диагональная матрица называется скалярной, если все ее элементы, принадлежащие главной диагонали, равны
- 9. Виды матриц Опр. 10. Прямоугольная матрица называется верхней трапециедальной, если m Опр. 11. Прямоугольная матрица с
- 10. Матрицы и основные операции над ними Опр. 12. Две матрицы А и В равны, если у
- 11. Матрицы и основные операции над ними Над матрицами определены три двухместные операции 1. Сложение матриц Складываются
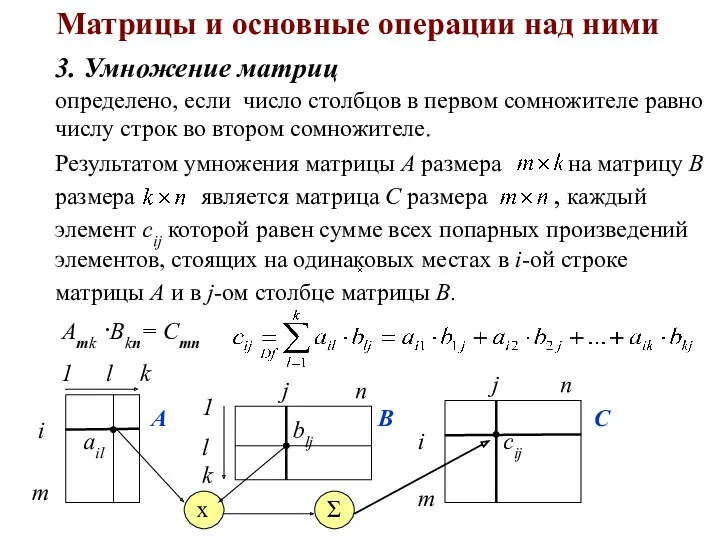
- 12. Матрицы и основные операции над ними 3. Умножение матриц определено, если число столбцов в первом сомножителе
- 13. Матрицы и основные операции над ними Умножение матриц имеет ряд свойств, что и у умножения чисел:
- 14. Свойства операций над матрицами Большинство свойств (при соответствующих размерах матриц) аналогичны свойствам операций над числами: Однако
- 15. Геометрическая интерпретация векторов Опр. 13. Геометрическим вектором на плоскости (в пространстве) с прямоугольной системой координат называется
- 16. Геометрическая интерпретация векторов Результаты операций над геометрическими векторами соответствуют результатам операций над соответствующими алгебраическими векторами.
- 17. Определитель квадратной матрицы Важнейшей числовой характеристикой квадратной матрицы является ее определитель (детерминант). В общем случае определитель
- 18. Определитель квадратной матрицы 1-го и 2-го порядка n=1. A=(a11) detA= a11 = a11 n=2.
- 20. Скачать презентацию














 Урок обобщение В царстве Измерений
Урок обобщение В царстве Измерений Масштаб. Урок математики. 6 класс
Масштаб. Урок математики. 6 класс Делители и кратные. 6 класс
Делители и кратные. 6 класс Презентация Геометрические фигуры
Презентация Геометрические фигуры Определение, предел, непрерывность ФМП. Частные производные, их геометрический смысл. Лекция 19
Определение, предел, непрерывность ФМП. Частные производные, их геометрический смысл. Лекция 19 Путешествие на планету положительных и отрицательных чисел. (6 класс)
Путешествие на планету положительных и отрицательных чисел. (6 класс) Математические фокусы. 7 класс
Математические фокусы. 7 класс Конспект урока математики 2 класс по системе Занкова (И.И.Аргинская) Тема урока: Умножение
Конспект урока математики 2 класс по системе Занкова (И.И.Аргинская) Тема урока: Умножение Порядок выполнения действий в математике
Порядок выполнения действий в математике Объемы тел. Площадь
Объемы тел. Площадь Единицы массы и времени
Единицы массы и времени Физикалық дамуды бағалау үшін регрессия және корреляцияны қолдану
Физикалық дамуды бағалау үшін регрессия және корреляцияны қолдану Дидактическая игра на уроке математики в 1 классе
Дидактическая игра на уроке математики в 1 классе Рационал өрнектер
Рационал өрнектер Умножение десятичных дробей
Умножение десятичных дробей Статистика
Статистика Основное свойство дроби. 6 класс
Основное свойство дроби. 6 класс Прямая и отрезок
Прямая и отрезок Урок по математике в 3 классе
Урок по математике в 3 классе Презентация к уроку математики (Школа 2100 3 класс)
Презентация к уроку математики (Школа 2100 3 класс) Игра для умных, веселых и находчивых. Задания
Игра для умных, веселых и находчивых. Задания Урок математики в 3 классе Письменные приемы сложения и вычитания трехзначных чисел посвященный Дню Космонавтики.
Урок математики в 3 классе Письменные приемы сложения и вычитания трехзначных чисел посвященный Дню Космонавтики.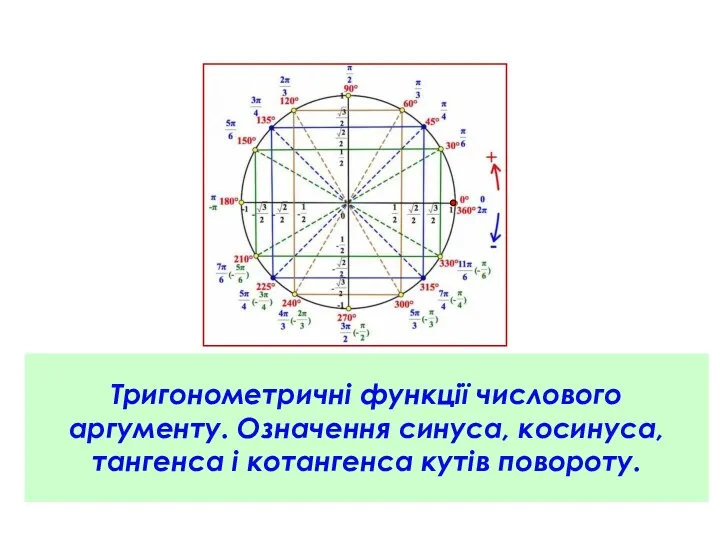 Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2
Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2 Презентация к уроку математики по теме: Нахождение неизвестного множителя. 3 класс УМК Перспективная начальная школа
Презентация к уроку математики по теме: Нахождение неизвестного множителя. 3 класс УМК Перспективная начальная школа Графический метод решения уравн
Графический метод решения уравн Умножение дробей. Знакомство с друзьями из Британии
Умножение дробей. Знакомство с друзьями из Британии Метод математических моделей в экономике
Метод математических моделей в экономике Метрология, стандартизация, сертификация. Основы метрологии
Метрология, стандартизация, сертификация. Основы метрологии