Матрицы: элементарные преобразования строк, приведение к ступенчатому виду и виду Гаусса. Ранг матрицы презентация
Содержание
- 2. Опр. 1 Элементарными преобразованиями строк матрицы называются: 1) Перестановка местами двух строк 2) Замена строки суммой
- 3. Аналогично вводятся элементарные преобразования столбцов. Опр.2 Опорным элементом строки называется первый слева ненулевой элемент этой строки.
- 4. Пример. У нулевой строки опорного элемента нет
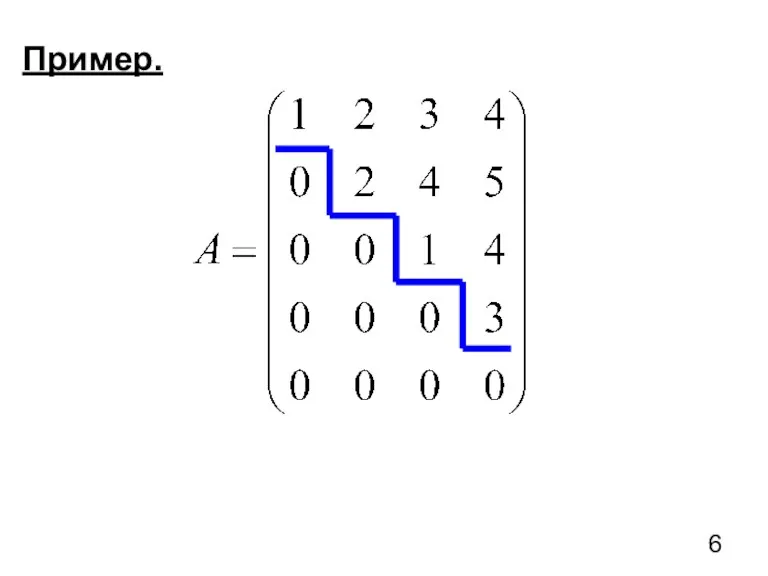
- 5. Опр. 3 Матрица называется ступенчатой, если опорный элемент в каждой последующей строке расположен правее, чем в
- 6. Пример.
- 7. Опр. 4 Матрица имеет вид Гаусса, если 1) она ступенчатая 2) все опорные элементы равны единице
- 8. Пример.
- 9. Теорема 4 Любая матрица может быть приведена к ступенчатому виду с помощью элементарных преобразований. Опр. 5
- 10. Опр. 6 Рангом матрицы называется число ненулевых строк в ступенчатом виде матрицы. Обозначается
- 13. Решение систем линейных уравнений. Метод Гаусса Пример.
- 14. 1) Составим расширенную матрицы системы
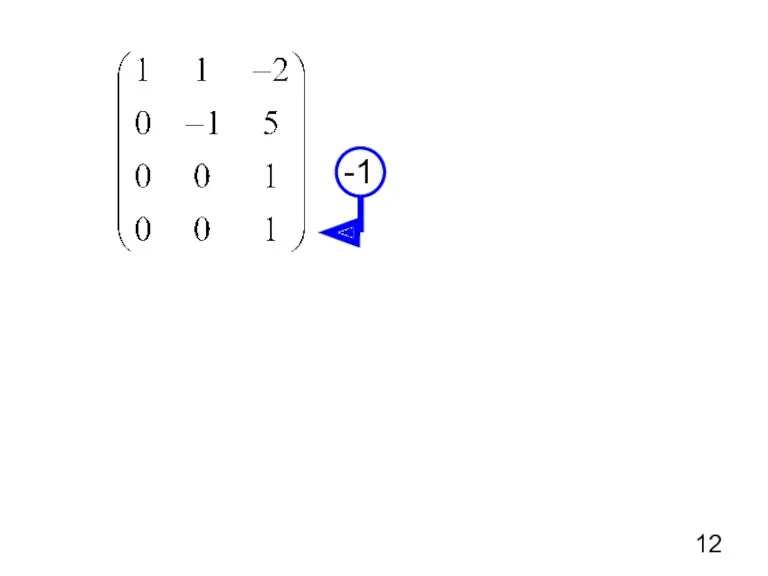
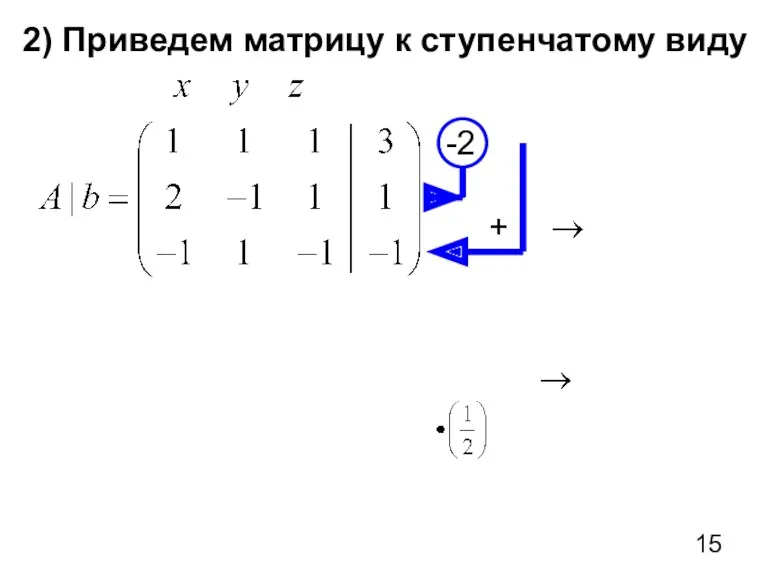
- 15. 2) Приведем матрицу к ступенчатому виду
- 17. 3) Составим новую систему Система имеет единственное решение Можно было продолжить преобразования, и привести систему к
- 18. Теорема Кронекера-Капелли.
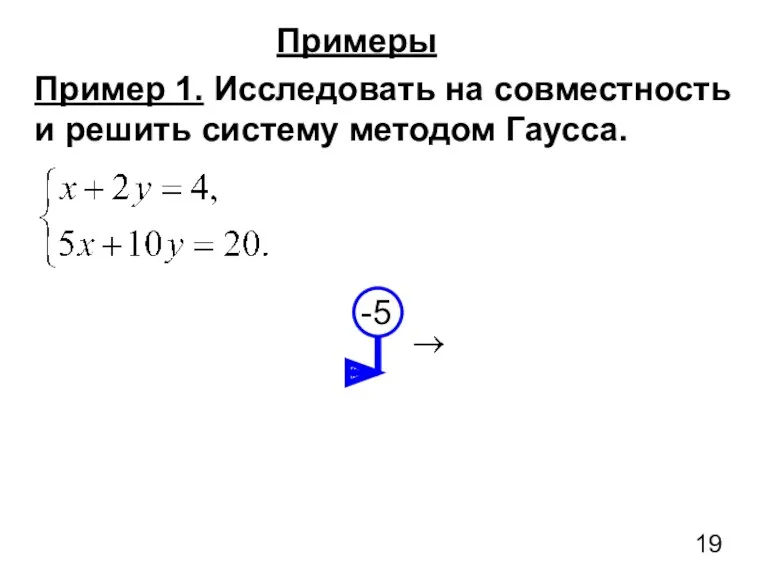
- 19. Примеры Пример 1. Исследовать на совместность и решить систему методом Гаусса.
- 20. Система имеет бесконечное множество решений. Найдем число свободных неизвестных
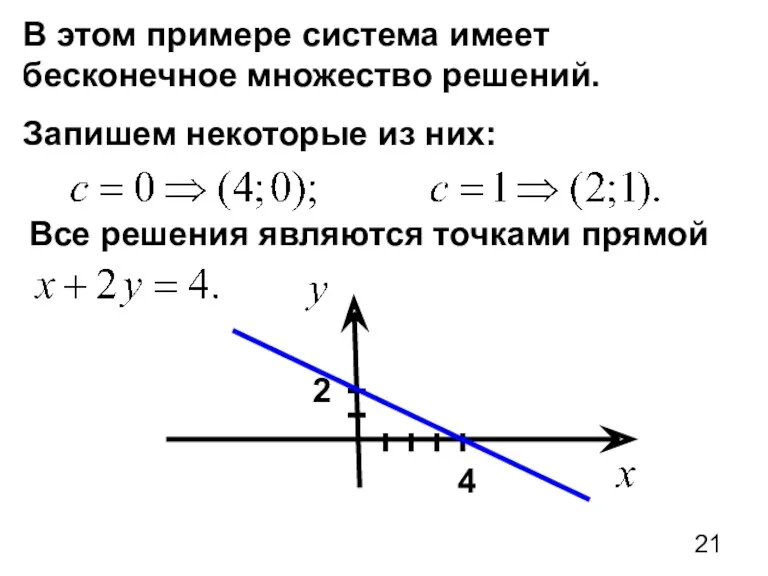
- 21. В этом примере система имеет бесконечное множество решений. Запишем некоторые из них:
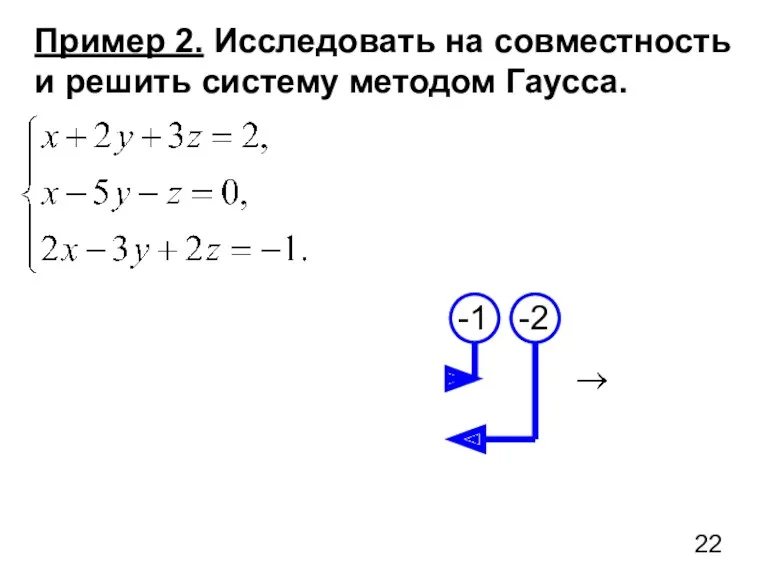
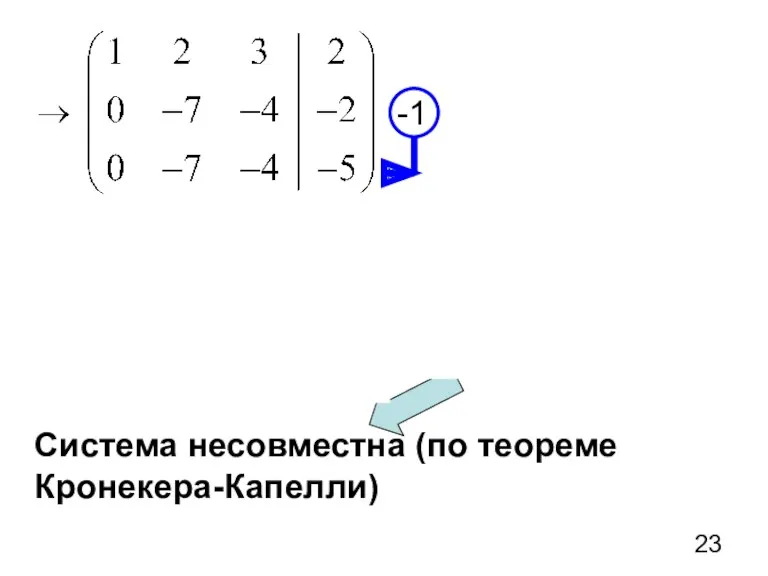
- 22. Пример 2. Исследовать на совместность и решить систему методом Гаусса.
- 23. Система несовместна (по теореме Кронекера-Капелли)
- 24. Мы рассмотрели два метода решения систем линейных уравнений: 1) Метод Крамера 2) Метод Гаусса Метод Крамера
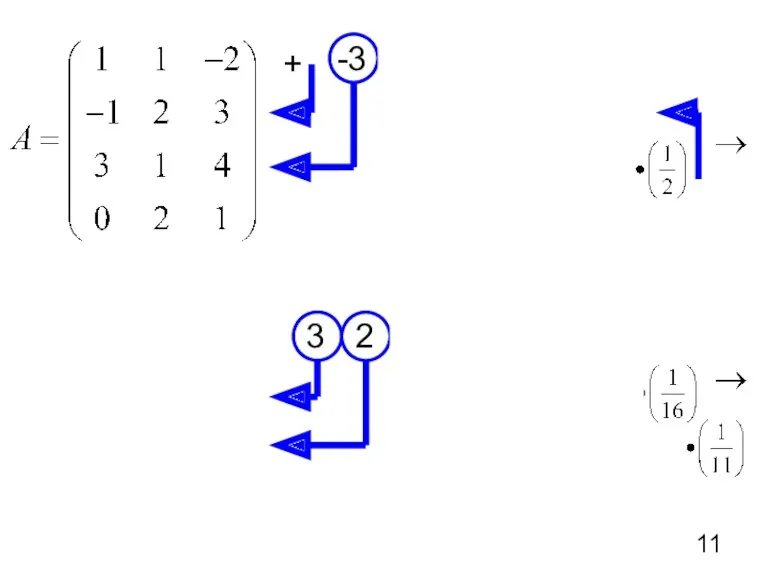
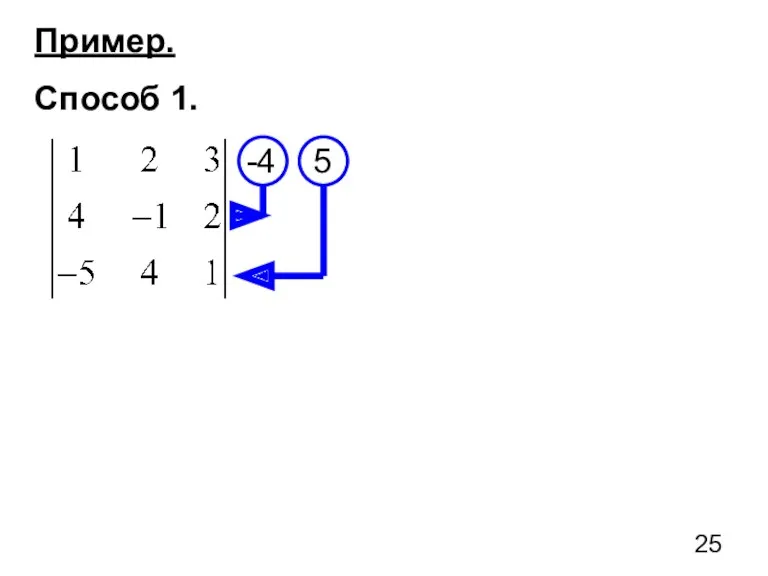
- 25. Пример. Способ 1. -4 5
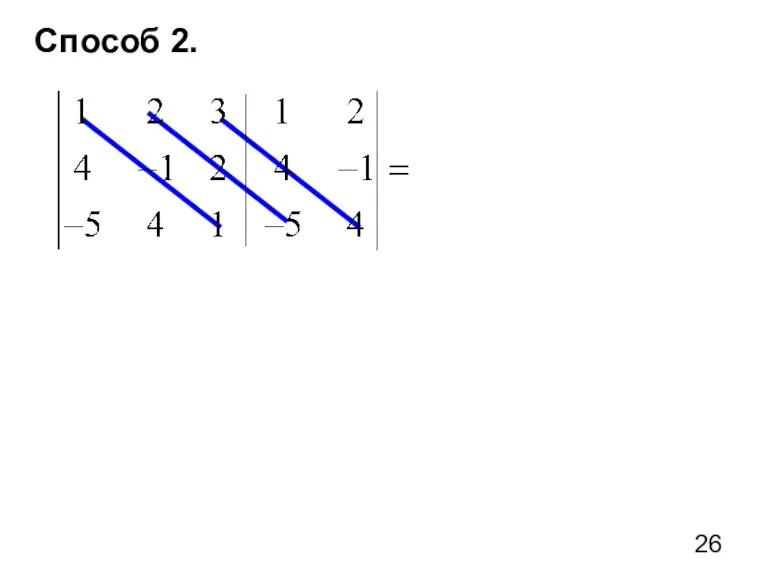
- 26. Способ 2.
- 27. 1) Определитель не изменится, если поменять строки на соответствующие столбцы Свойства определителей 2) Если у определителя
- 28. 4) Если две строки (столбца) поменять местами, то знак определителя изменится на противоположный. Свойства определителей 5)
- 30. Скачать презентацию





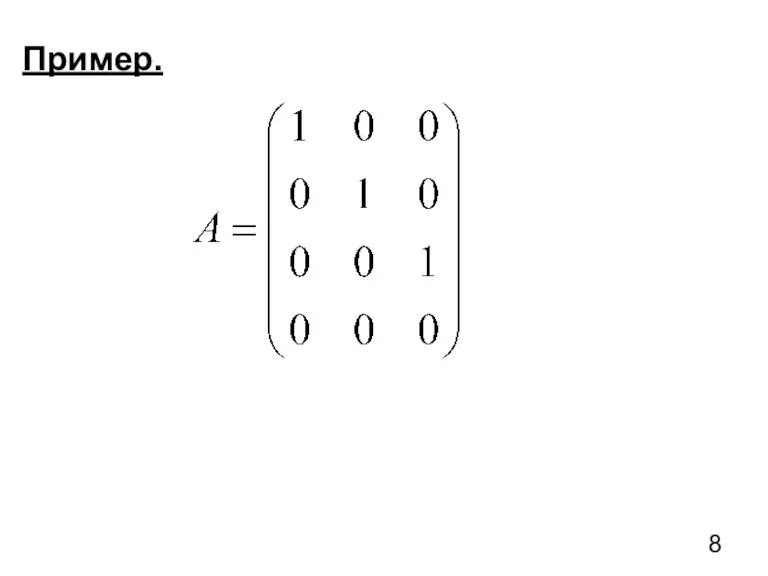











 Дроби. Выражения
Дроби. Выражения Координаты на прямой
Координаты на прямой интерактивная физминутка для глаз
интерактивная физминутка для глаз График функции
График функции математика
математика Решение задач на движение
Решение задач на движение Применение производной в науке и технике
Применение производной в науке и технике Случаи вычитания 14 -
Случаи вычитания 14 - Средства измерений и их классификация. Лекция 2
Средства измерений и их классификация. Лекция 2 Равнобедренный треугольник
Равнобедренный треугольник Мир геометрии
Мир геометрии Наибольший общий делитель. 6 класс
Наибольший общий делитель. 6 класс Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Приращение аргумента, приращение функции
Приращение аргумента, приращение функции Логические блоки Дьенеша
Логические блоки Дьенеша Решение неравенств с одной переменной и решение систем неравенств
Решение неравенств с одной переменной и решение систем неравенств Правила вычисления производных
Правила вычисления производных Открытый урок по математике в 3-м классе Единица времени - сутки
Открытый урок по математике в 3-м классе Единица времени - сутки Распределительное свойство умножения
Распределительное свойство умножения Удивительная наука геометрия
Удивительная наука геометрия Определенный интеграл и его свойства. Формула Ньютона-Лейбница
Определенный интеграл и его свойства. Формула Ньютона-Лейбница Решение заданий В10 по материалам открытого банка задач ЕГЭ по математике 2013 года
Решение заданий В10 по материалам открытого банка задач ЕГЭ по математике 2013 года Регрессиялық талдау
Регрессиялық талдау Сложение, вычитание обыкновенных дробей с разными знаменателям
Сложение, вычитание обыкновенных дробей с разными знаменателям Раскрытие скобок
Раскрытие скобок Мультимедийное дидактическое пособие для детей 5 - 6 лет по формированию элементарных математических предствалений Приключение паровозика ЧУХ – ЧУХ в стране математики
Мультимедийное дидактическое пособие для детей 5 - 6 лет по формированию элементарных математических предствалений Приключение паровозика ЧУХ – ЧУХ в стране математики Внеклассное Математическое ассорти. 6 класс
Внеклассное Математическое ассорти. 6 класс Функции нескольких переменных
Функции нескольких переменных