Матрицы, операции над матрицами, теорема существования обратной матрицы. Матричная запись систем линейных уравнений презентация
Содержание
- 2. §1. Матрицы и действия над ними. Определение. Матрица – прямоугольная таблица из m×n действительных чисел, расположенных
- 3. Матрица, все элементы которой нули, называется нулевой. Матрицы у которых соответственно равны числа строк и столбцов
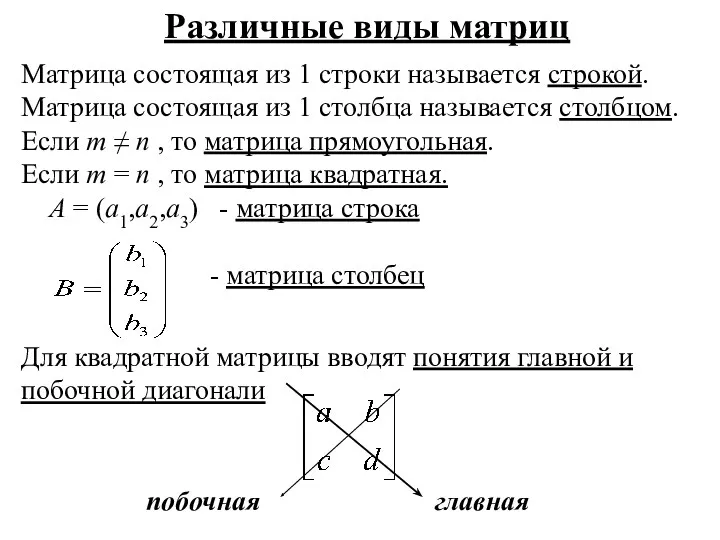
- 4. Различные виды матриц Матрица состоящая из 1 строки называется строкой. Матрица состоящая из 1 столбца называется
- 5. Матрица у которой отличны от нуля лишь элементы главной диагонали называется диагональной. Диагональная матрица у которой
- 6. Операции над матрицами 1.) Транспонирование – замена всех строк матрицы столбцами с сохранением номеров (At) для
- 7. 2.2. Произведением Amxn на λ ϵ R (или λ ϵ R на А) называется Bmxn[bij], bij
- 8. План доказательства. 1.) Показать, что матрицы слева и справа имеют один и тот же размер 2.)
- 9. В общем случае AB ≠ BA, если AB = BA, то матрицы А и В называются
- 10. Свойства операции умножения. Предположим, что все указанные операции выполнимы
- 11. §2. Обратная матрица. Матричные уравнения. Формулы Крамера. Теорема об определителе квадратных матриц. Теорема: Определитель произведения двух
- 12. (2) Определение квадратной матрицы. Определение: Квадратная матрица А называется вырожденной (особенной), если ее определитель = 0
- 13. Необходимость. Пусть А имеет обратную В. Тогда по определению АВ = ВА = Е, АВ =
- 14. Единственность обратной матрицы. Теорема: Если А имеет обратную, то она (обратная) единственная. Доказательство: Пусть В обратная
- 15. Так как В обратная для А, то АВ = Е Умножим обе части равенства слева на
- 16. Свойства обратной матрицы.
- 17. Матричные уравнения. Матричными уравнениями называются уравнения вида: АХ = В (1) ХС = D (2), где
- 18. т.к. |С| ≠ 0, то С-1 существует. Умножим обе части уравнения (2) слева на С-1. С-1(ХС)
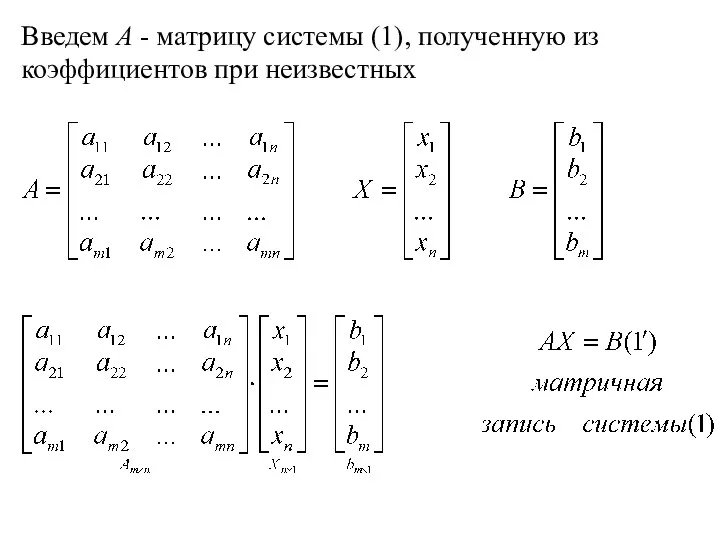
- 19. Введем А - матрицу системы (1), полученную из коэффициентов при неизвестных
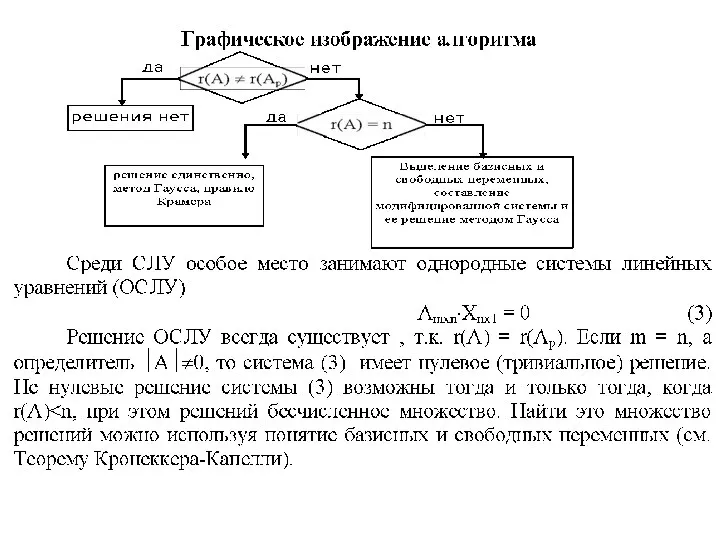
- 21. Замечание: неизвестные и свободные члены можно расположить в строки, то запись имела бы соответствующий вид. Теорема
- 22. Составим определитель из коэффициентов при неизвестных - определитель системы. Теорема. Если определитель квадратной системы отличен от
- 23. Δ - определитель системы Δk (k = 1,2…) - определитель, полученный из определителя системы заменой k-ого
- 34. Лекция 4. Определение линейного пространства. Аксиомы, линейная зависимость и независимость векторов. Базис и размерность линейного пространства;
- 55. Скачать презентацию
















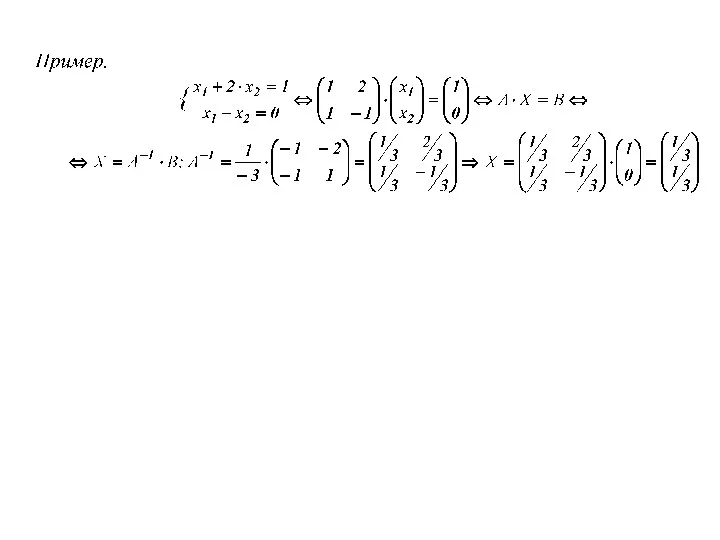
































 Подготовка к ЕГЭ по математике. Решение задач В12
Подготовка к ЕГЭ по математике. Решение задач В12 Производная функции
Производная функции Подготовка к итоговой аттестации по математике в 9 классе
Подготовка к итоговой аттестации по математике в 9 классе Ehtimalın klassik tərifi
Ehtimalın klassik tərifi Лекция 1.2. Классическое определение вероятности
Лекция 1.2. Классическое определение вероятности Формулы в математике
Формулы в математике Решение задач в два действия. 1 класс
Решение задач в два действия. 1 класс Метод середніх величин
Метод середніх величин Признаки параллельности прямых. Тест. Задачи
Признаки параллельности прямых. Тест. Задачи Решение задач с помощью уравнений
Решение задач с помощью уравнений Выражения со скобками
Выражения со скобками Тест по теме: Объем шара и площадь сферы
Тест по теме: Объем шара и площадь сферы Проектная работа Математическая сказка для 4 класса.
Проектная работа Математическая сказка для 4 класса. Презентация к уроку математики Приметр многоугольника.
Презентация к уроку математики Приметр многоугольника. Отрезок и ломаная. УМК Планета знаний, 1 класс.
Отрезок и ломаная. УМК Планета знаний, 1 класс. урок математики 3 класс Сложение и вычитание величин
урок математики 3 класс Сложение и вычитание величин Теорема Виета. 8 класс
Теорема Виета. 8 класс Параллельность прямой и плоскости. Решение задач
Параллельность прямой и плоскости. Решение задач Устное умножение круглых сотен. 1 часть
Устное умножение круглых сотен. 1 часть Пирамида. Правильная пирамида
Пирамида. Правильная пирамида Дифференциальное и интегральное исчисление
Дифференциальное и интегральное исчисление Электронно-демонстрационная игра
Электронно-демонстрационная игра Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Координатная плоскость
Координатная плоскость Экономико-математические методы и модели в логистике
Экономико-математические методы и модели в логистике Усеченная пирамида
Усеченная пирамида Приемы коррекционного обучения детей с ОВЗ на уроках математики
Приемы коррекционного обучения детей с ОВЗ на уроках математики Показательная функция, ее свойства и график
Показательная функция, ее свойства и график