Содержание
- 2. План лекции Дифференциал функции. Геометрический смысл дифференциала. Частные производные. Полный дифференциал. Понятие первообразной функции. Неопределенный интеграл.
- 3. Значение темы Понятие производной и интеграла широко используется в математике, статистике и прикладных науках. С их
- 4. Понятие производной Производной функции f(x) называется предел отношения приращения функции к приращению аргумента при стремлении последнего
- 5. Правила дифференцирования производная сложной функции
- 6. Таблица производных от основных функций
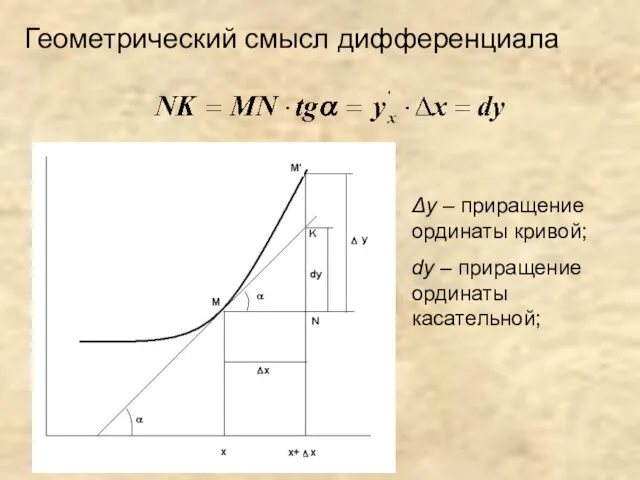
- 7. Δy – приращение ординаты кривой; dy – приращение ординаты касательной; Геометрический смысл дифференциала
- 8. Дифференциал Дифференциал dy - главная часть приращения функции Δy Дифференциалом dx называют приращение Δx, то есть
- 9. Правила дифференцирования
- 10. Частные производные
- 11. Использование дифференциала в приближенных вычислениях Для нахождения приближенного значения приращения функции Для нахождения приближенного значения функции
- 12. Основные характеристики и свойства функции Y=f(X) Область значений y и х Постоянство или монотонность функции на
- 13. Постоянство и монотонность функции Для того чтобы функция f(x) была постоянной на отрезке [a,b], нужно, чтобы
- 14. Нули функции: решения уравнения Y(X) =0 Полюса функции: значения Х, при котором Y стремится к бесконечности
- 15. Минимумы и максимумы функции Функция f(x) имеет в точке х0 минимум (максимум), если в некоторой окрестности
- 16. Правило нахождения экстремума
- 17. Перегибы, выпуклость и вогнутость функции Если вторая производная в точке М больше нуля, то кривая в
- 18. Первообразная функции Прямая задача: известно уравнение движения s=s(t); найти скорость v=ds/dt и ускорение dv/dt Обратная задача:
- 19. Свойства операции интегрирования Закон инерции Ньютона: как, зная уравнение для второго закона Ньютона, найти уравнение для
- 20. Таблица интегралов основных функций
- 21. Пример:
- 22. Интегрирование путем замены переменной
- 23. Интегрирование по частям
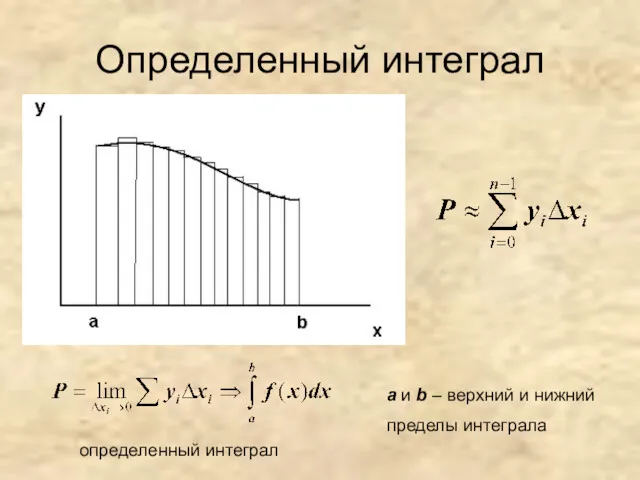
- 24. Определенный интеграл a и b – верхний и нижний пределы интеграла определенный интеграл
- 25. Свойства определенного интеграла
- 26. Основная формула интегрального исчисления F(x) – первообразная f(x)
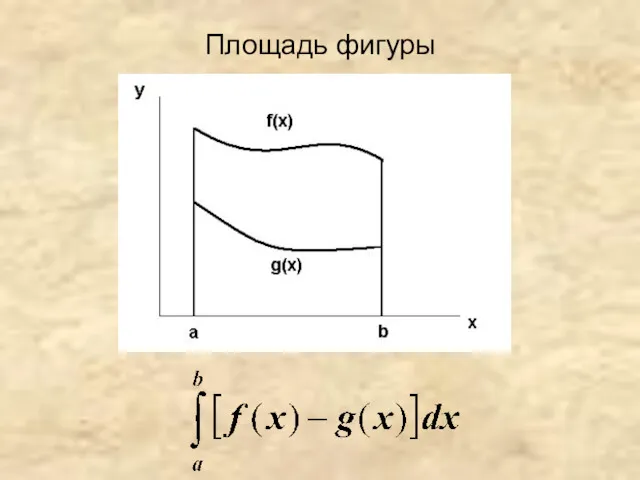
- 27. Площадь фигуры
- 28. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Обязательная: Кричевец, А.Н. Математика для психологов /А.Н. Кричевец, Е.В. Шикин, А.Г. Дьячков. – М.:
- 30. Скачать презентацию


















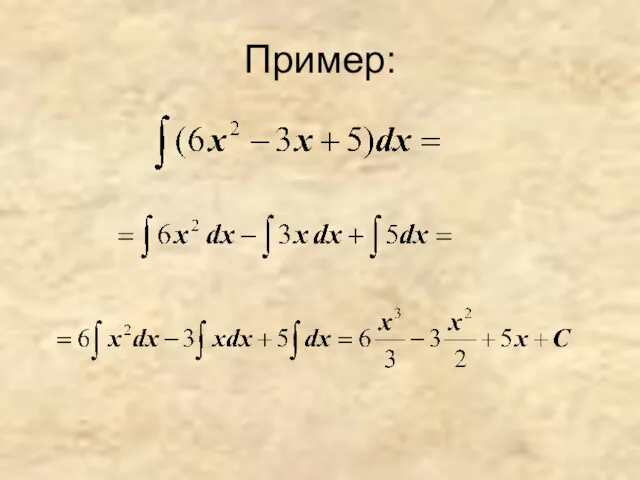





 Математическая игра для 5–6 классов. Математик-бизнесмен
Математическая игра для 5–6 классов. Математик-бизнесмен Sisteme determinate de ecuaţii algebrice liniare
Sisteme determinate de ecuaţii algebrice liniare Бөлшектік еселікпен резервтеу. Көпшілік дауыс беру бойынша резервтеу. Лекция №5
Бөлшектік еселікпен резервтеу. Көпшілік дауыс беру бойынша резервтеу. Лекция №5 Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия
Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Напівправильні многогранники
Напівправильні многогранники Графики функций y=ax2+n и y=a(x-m)2
Графики функций y=ax2+n и y=a(x-m)2 Отчет о математической декаде
Отчет о математической декаде Устный счет. Сложение с переходом через десяток. Часть 3
Устный счет. Сложение с переходом через десяток. Часть 3 Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Функция. Область определения и множество значений функции
Функция. Область определения и множество значений функции Единицы измерения. Диск
Единицы измерения. Диск Готовимся к ГИА, 9 класс. Тест 2, часть 1
Готовимся к ГИА, 9 класс. Тест 2, часть 1 Таблица умножения
Таблица умножения Производная сложной функции
Производная сложной функции Соотношения между сторонами и углами треугольника. Задания для устного счета. Упражнение 11. 7 класс
Соотношения между сторонами и углами треугольника. Задания для устного счета. Упражнение 11. 7 класс Сложение чисел с разными знаками
Сложение чисел с разными знаками Задания на сравнение и счёт
Задания на сравнение и счёт Основные моменты тригонометрии
Основные моменты тригонометрии История возникновения интегралов. Историческая справка
История возникновения интегралов. Историческая справка Интерполяция, экстраполяция, аппроксимация
Интерполяция, экстраполяция, аппроксимация Координатная плоскость
Координатная плоскость Имитационные модели
Имитационные модели Математикадан ачык дәрес 4 класс
Математикадан ачык дәрес 4 класс Логарифмическая функция в уравнениях
Логарифмическая функция в уравнениях Средние величины
Средние величины Деление с остатком
Деление с остатком Презентация проекта Время и часы
Презентация проекта Время и часы