Содержание
- 2. ТЕОРЕМА Если y=f(u), u=φ(x) – дифференцируемые функции своих аргументов, то производная сложной функции существует и равна
- 3. Доказательство: Дадим аргументу х приращение Δх, не равное 0, тогда функции u=φ(x), y=f(u) получат приращения Δu
- 4. На основании теоремы о связи бесконечно малых величин с пределами функций функцию, стоящую под знаком предела,
- 5. Т.к. по условию функция u=φ(x) дифференцируема, то она непрерывна в точке x. Следовательно, при и Переходим
- 6. Правило дифференцирования сложной функции можно записать иначе: или
- 7. Примеры. 1 Найти производные сложных функций:
- 8. Решение:
- 9. 2
- 10. Решение:
- 12. Скачать презентацию









 Возведение в степень произведения и степени
Возведение в степень произведения и степени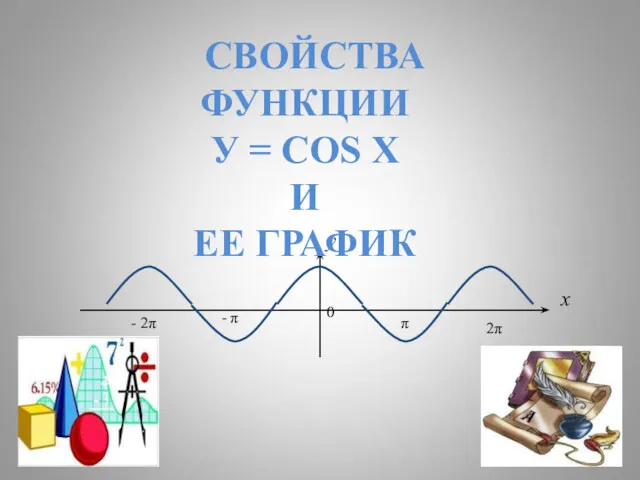 Свойства функции y=cos-x и ее график
Свойства функции y=cos-x и ее график Елементи теорії виміру. Шкали виміру. Лекція 6. Тема 3
Елементи теорії виміру. Шкали виміру. Лекція 6. Тема 3 Закрепление + - 3. Сравнение отрезков. 1 класс Школа России
Закрепление + - 3. Сравнение отрезков. 1 класс Школа России Степени и корни. Свойства степеней
Степени и корни. Свойства степеней Софья Ковалевская
Софья Ковалевская Числа 1 - 4
Числа 1 - 4 Метрология. Введение. Структура дисциплины
Метрология. Введение. Структура дисциплины grafy1
grafy1 Число и цифра 4.
Число и цифра 4. Тренажёр умножения на 2
Тренажёр умножения на 2 Статистическое распределение выборки и его основные числовые характеристики
Статистическое распределение выборки и его основные числовые характеристики Раскрытие скобок
Раскрытие скобок Медиа-сопровождение к уроку математики Число 9. Цифра 9
Медиа-сопровождение к уроку математики Число 9. Цифра 9 Урок математики для 2 класса Трёхзначные числа
Урок математики для 2 класса Трёхзначные числа НОД по математическому развитию в подготовительной группе.
НОД по математическому развитию в подготовительной группе. Решение обыкновенных дифференциальных уравнений (краевая задача)
Решение обыкновенных дифференциальных уравнений (краевая задача) Раскрытие скобок
Раскрытие скобок Цікаві факти з історії геометрії
Цікаві факти з історії геометрії Grafika komputerowa
Grafika komputerowa Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Формула пути. Решение задач на движение
Формула пути. Решение задач на движение Тест по теме: Тетраэдр и параллелепипед. Теория
Тест по теме: Тетраэдр и параллелепипед. Теория Система подготовки к ЕГЭ
Система подготовки к ЕГЭ Марковские системы массового обслуживания
Марковские системы массового обслуживания Логарифмы вокруг нас. История логарифмов
Логарифмы вокруг нас. История логарифмов Три точки зрения на геометрию вселенной
Три точки зрения на геометрию вселенной Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс
Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс