Содержание
- 2. Содержание Математическое моделирование, вычислительный эксперимент и МКЭ. Общие сведения о МКЭ (история, особенности, общая схема) Уравнение
- 3. Основная литература Деклу Ж. Метод конечных элементов, перев. с фр. М.: Мир, 1976. 96 с. (http://eqworld.ipmnet.ru/ru/library/books/Deklu1976ru.djvu).
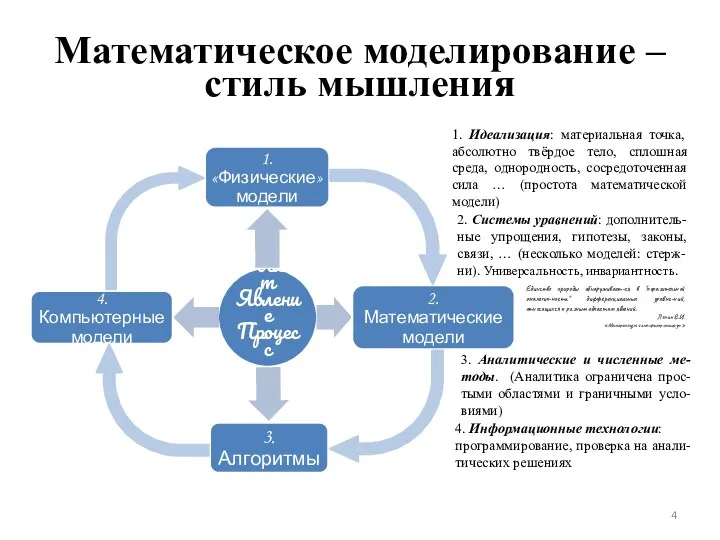
- 4. Математическое моделирование – стиль мышления 1. Идеализация: материальная точка, абсолютно твёрдое тело, сплошная среда, однородность, сосредоточенная
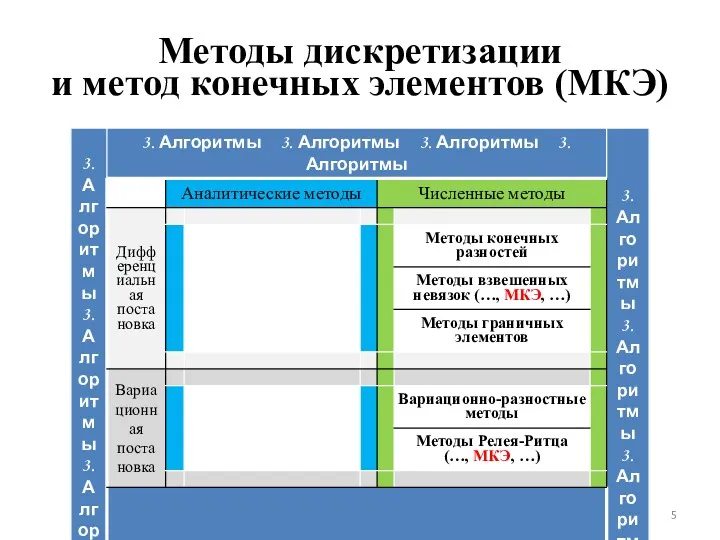
- 5. Методы дискретизации и метод конечных элементов (МКЭ)
- 6. Семейство «Метод взвешенных невязок» (МВН) Аппроксимация Дано: Аппроксимировать за-данную функцию f в об-ласти Ω, ограниченной поверхностью
- 7. Семейство «Метод взвешенных невязок» (МВН) Дано: Найти решение дифферен-циального уравнения в об-ласти Ω, ограниченной по-верхностью ∂Ω,
- 8. Семейство «Метод взвешенных невязок» (МВН) Метод коллокации (базисные функции – любые; коллокация в точке: весовые функции
- 9. Семейство «Метод Релея-Ритца» (МРР) Решение вариационных задач Дано: Найти функцию u принадле-жащую подпространству до-пустимых функций W
- 10. Исторические сведения о МКЭ … 1877 Рэлей (Sir John William Strutt, Lord Rayleigh) - приближённое решение
- 11. Исторические сведения о МКЭ Ива́н Григо́рьевич Бу́бнов (06(18).01.1872–13.03.1919) – российский корабельный инженер и математик. Впервые указал
- 12. Общая схема МКЭ Рассматриваемая область разделяется на ряд простых по форме конечных подобластей, которые называются конечными
- 13. Преимущества и недостатки МКЭ Применим для задач аппроксимации функций, решения дифференциальных уравнений, вариационных задач, стационарных и
- 14. Уравнение теплопроводности Первый закон термодинамики (закон баланса энергии) для недиссипативных сред представляет собой уравнение распространения тепла
- 15. Уравнение теплопроводности В изотропном для тепловых процессов материале тензор удельной теплопровод-ности K – шаровой: k –
- 16. Уравнение теплопроводности Уравнение нестационарной теплопроводности содержит производную первого порядка по времени и произ-водные второго порядка по
- 17. Вариационная постановка задачи теплопроводности ______________________________________________________________________ Уравнения Эйлера-Лагранжа-Остроградского (1750-е годы – Л.Эйлер, Ж.Л.Лагранж, 1834 – М.В.Остроградский)
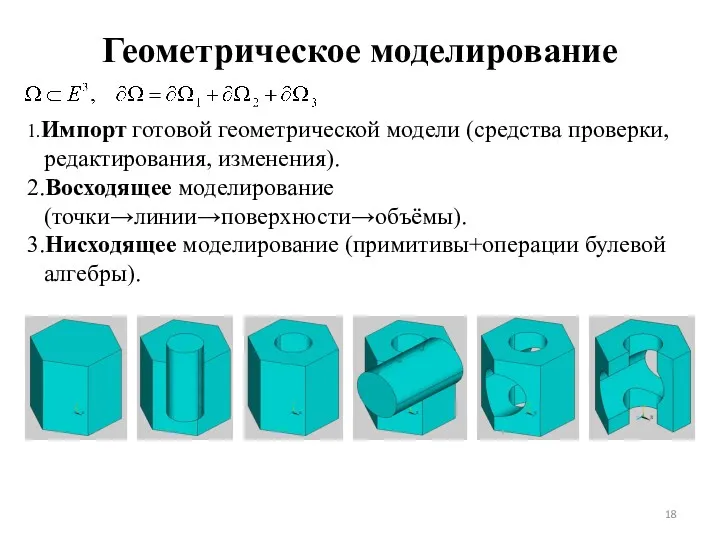
- 18. Геометрическое моделирование 1.Импорт готовой геометрической модели (средства проверки, редактирования, изменения). 2.Восходящее моделирование (точки→линии→поверхности→объёмы). 3.Нисходящее моделирование (примитивы+операции
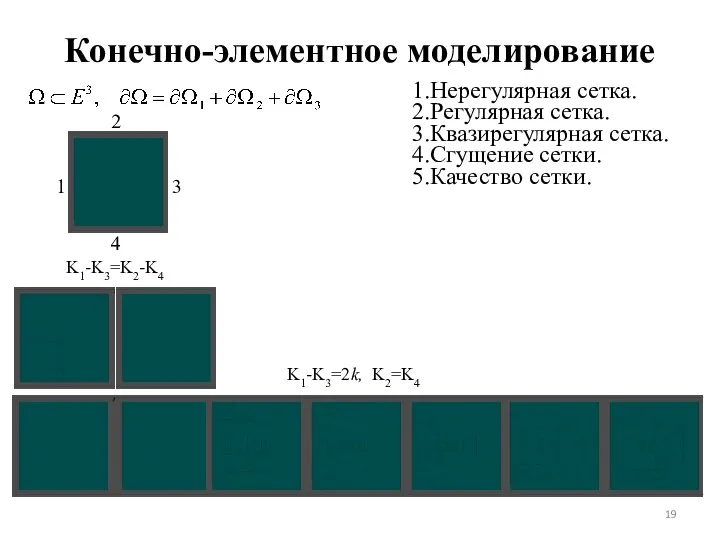
- 19. Конечно-элементное моделирование 1.Нерегулярная сетка. 2.Регулярная сетка. 3.Квазирегулярная сетка. 4.Сгущение сетки. 5.Качество сетки. K1-K3=K2-K4 K1-K3=2k, K2=K4
- 21. Скачать презентацию














 Из истории дроби. Современное обозначение дробей
Из истории дроби. Современное обозначение дробей Презентация к уроку математики 2 класс
Презентация к уроку математики 2 класс Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби Вычитание групп предметов
Вычитание групп предметов Сфера, вписанная в многогранник
Сфера, вписанная в многогранник 20231004_prezentatsiya_doli._obyknovennye_drobi
20231004_prezentatsiya_doli._obyknovennye_drobi Взаимное расположение плоскостей, прямой и плоскости на чертежах
Взаимное расположение плоскостей, прямой и плоскости на чертежах Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Решение уравнений
Решение уравнений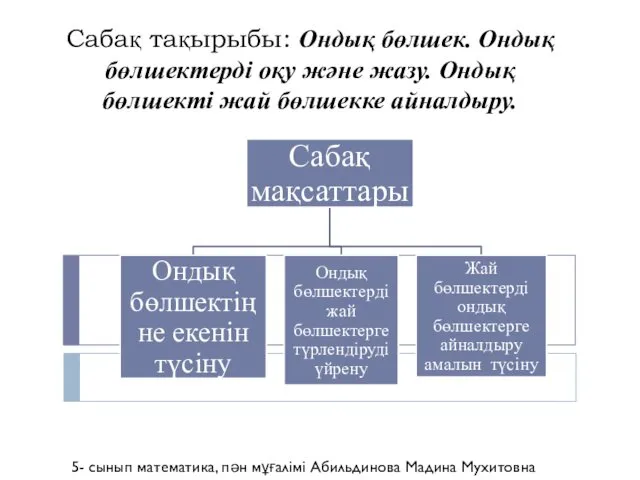 Ондық бөлшек. Ондық бөлшектерді оқу және жазу. Ондық бөлшекті жай бөлшекке айналдыру
Ондық бөлшек. Ондық бөлшектерді оқу және жазу. Ондық бөлшекті жай бөлшекке айналдыру Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Фиктивные переменные в регрессионных моделях
Фиктивные переменные в регрессионных моделях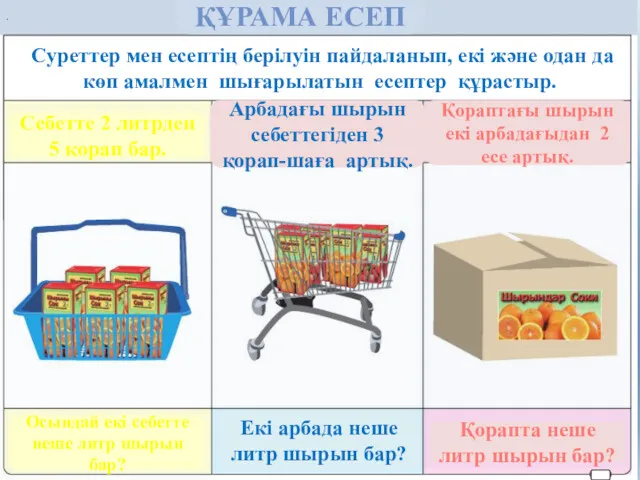 Құрама есеп
Құрама есеп Решение задач по теме Многогранники
Решение задач по теме Многогранники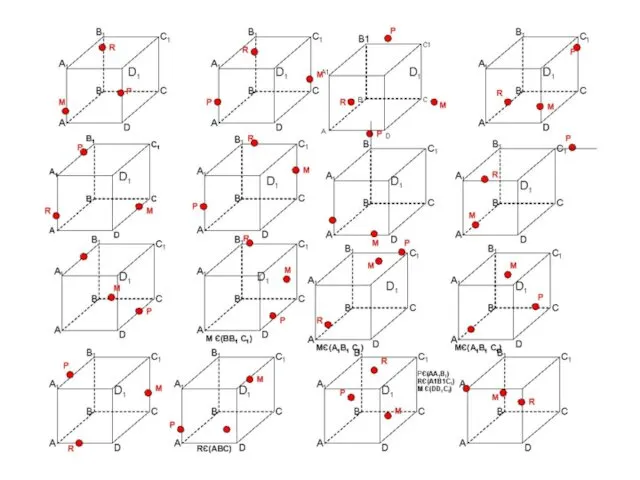 Постороение сечений
Постороение сечений Линейные однородные дифференциальные уравнения (ЛОДУ) 2 порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения (ЛОДУ) 2 порядка с постоянными коэффициентами Ряды динамики
Ряды динамики Гетероскедастичность и ее последствия
Гетероскедастичность и ее последствия Модуль числа
Модуль числа Интеграл от функции комплексного переменного. Теорема Коши. Бесконечная дифференцируемость аналитической функции
Интеграл от функции комплексного переменного. Теорема Коши. Бесконечная дифференцируемость аналитической функции Презентация к уроку математики в 1 классе. Устный счёт.
Презентация к уроку математики в 1 классе. Устный счёт. Векторная алгебра (лекция 11)
Векторная алгебра (лекция 11) Интегрированный урок математики и окружающего мира в 1 классе УМК Гармония
Интегрированный урок математики и окружающего мира в 1 классе УМК Гармония Задачи на построение треугольника
Задачи на построение треугольника Презентация для изучения темы Площадь
Презентация для изучения темы Площадь Логарифмы вокруг нас
Логарифмы вокруг нас Задачи на разрезание
Задачи на разрезание