Содержание
- 2. В основе всякого математического исследования лежит дедуктивный и индуктивный методы обоснования того или иного утверждения.
- 3. Дедукция – переход от общих утверждений к частным. Пример Все граждане России имеют право на образование.
- 4. Индукция – переход от частных утверждений к общим. Пример 140 делится на 5. Все числа, оканчивающиеся
- 5. Рассмотрим пример рассуждения по индукции: Требуется установить, что Каждое четное натуральное число в пределах от 4
- 6. Это полная индукция, когда общее утверждение доказывается для конечного множества элементов рассмотрением каждого элемента множества по
- 7. Примеры 1) Рассмотрим суммы первых n нечетных натуральных чисел: Выдвинем гипотезу, что всегда сумма первых n
- 8. Проверим ее для шести и семи слагаемых: Гипотеза подтвердилась. Но всё равно утверждение остается гипотезой, пока
- 9. 2) Рассмотрим последовательность yn = n2 + n + 17. Все полученные числа простые. y1 =
- 10. Есть в последовательности числа, не являющиеся простыми, например: y16 = 162 + 16 + 17 =
- 11. Во многих случаях выход заключается в обращении к особому методу рассуждений, который называют методом математической индукции.
- 12. Принцип математической индукции Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены два
- 13. Пример 1 Доказать, что 1) для n = 1 2) предположим, что равенство (1) выполняется при
- 14. Само по себе равенство (3) нас не интересует, нас интересует только один вопрос: вытекает ли оно
- 15. Итак, из равенства (2) вытекает равенство (3). Оба условия принципа математической индукции выполняются, значит, равенство (1)
- 16. Пример 2 Доказать, что 1) для n = 1 2) при n = k верно равенство:
- 17. Заменив сумму кубов в левой части равенства (6) правой частью равенства (5), получим:
- 18. Итак, из равенства (5) вытекает равенство (6). Оба условия принципа математической индукции выполняются, значит, равенство (4)
- 19. Пример 3 Найти сумму Решение: Обозначим заданную сумму символом Sn и найдем ее значение при n
- 20. Докажем справедливость этой формулы методом математической индукции. Для n = 1 формула справедлива. Предположим, что ,
- 21. Заметим, что в этом примере можно было обойтись без метода математической индукции:
- 22. Иногда требуется доказать некоторое утверждение не для всех натуральных чисел n, а для n ≥ p.
- 23. Пример 4 Доказать, что для n ≥ 2 и x > 0 справедливо неравенство Решение: (его
- 24. т.е. докажем, что Умножив обе части неравенства (7) на одно и то же положительное число 1
- 26. Скачать презентацию
 Решение задач. Масса одного предмета, количество, общая масса
Решение задач. Масса одного предмета, количество, общая масса Метрологические характеристики СИ
Метрологические характеристики СИ Перпендикулярные прямые
Перпендикулярные прямые Вычисление периметра прямоугольника.Математика.2класс
Вычисление периметра прямоугольника.Математика.2класс Пифагор Самосский
Пифагор Самосский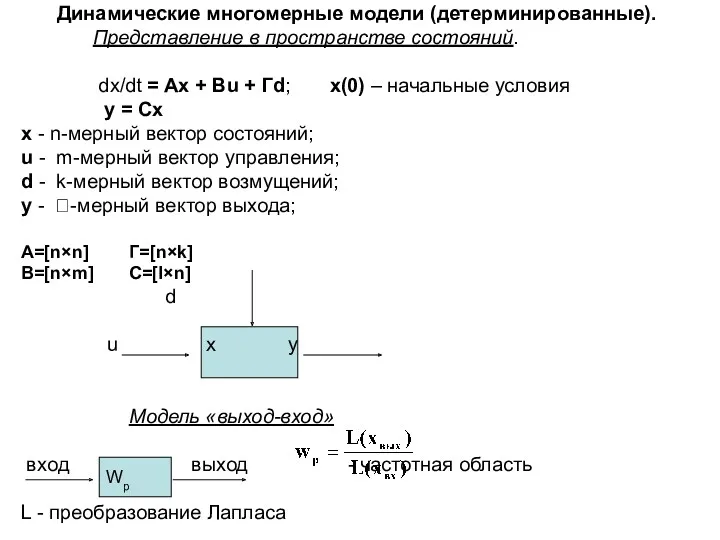 Динамические многомерные модели (детерминированные)
Динамические многомерные модели (детерминированные) Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Представление числовой информации в таблицах. Часть 2
Представление числовой информации в таблицах. Часть 2 Презентация Прощай, 1 класс
Презентация Прощай, 1 класс Методическая разработка по математике Прямоугольный параллелепипед. Его развёртка
Методическая разработка по математике Прямоугольный параллелепипед. Его развёртка Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса Математический тренажёр по теме Числа от 11 до 20: нумерация, состав числа 1 класс.
Математический тренажёр по теме Числа от 11 до 20: нумерация, состав числа 1 класс. ЕГЭ профильная математика. Задание № 4
ЕГЭ профильная математика. Задание № 4 урок математики Вычитание из 8 и 9
урок математики Вычитание из 8 и 9 Презентация внеклассного занятия по математике 4 класс Самый умный
Презентация внеклассного занятия по математике 4 класс Самый умный Веселый счет
Веселый счет Четырехугольники. Подготовка к ОГЭ
Четырехугольники. Подготовка к ОГЭ Этапы расчета прогнозных значений с помощью корреляционно-регрессионного анализа (многофакторная модель)
Этапы расчета прогнозных значений с помощью корреляционно-регрессионного анализа (многофакторная модель) Математика. 1 класс. Урок 69. Уравнение - Презентация
Математика. 1 класс. Урок 69. Уравнение - Презентация Плоскость. Уравнения плоскости
Плоскость. Уравнения плоскости Понятие симметрии
Понятие симметрии Решение неравенств, содержащих модуль
Решение неравенств, содержащих модуль Выполнить деление
Выполнить деление Числа великаны. Сферы применения
Числа великаны. Сферы применения Линейная функция и её график. Упражнения
Линейная функция и её график. Упражнения Пирамида. Правильная пирамида
Пирамида. Правильная пирамида Последние цифры степеней
Последние цифры степеней Медиана числового набора. Устойчивость медианы. 7 класс
Медиана числового набора. Устойчивость медианы. 7 класс