Содержание
- 2. Методы разложения многочленов на множители. Вынесение множителя за скобку Использование формул сокращённого умножения Способ группировки Метод
- 3. Вынесение множителя за скобку. Из распределительного закона непосредственно следует, что ac + bc = c(a +
- 4. Использование формул сокращённого умножения. a2-b2=(a-b)(a+b); a3-b3=(a-b)(a2+ab+b2); a3+b3=(a+b)(a2-ab+b2); a2+2ab+b2=(a+b)2; a2-2ab+b2=(a-b)2. (а - b) 3 = а3 -
- 5. Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе
- 6. Метод разложения квадратного трехчлена на множители Пример: Разложить на множители квадратный трехчлен х2-6x+5 Решение х2-6x+5= (решим
- 7. 16x7 – 72x6 + 108x5 – 54x4 = = 2x4 (8x3 – 36x2 – 54) =
- 9. D=1-4*5*1=-19-нет корней
- 10. =
- 13. 1) ( ) Аналогично 2 и 3 система
- 17. Метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается
- 18. Схема Горнера. Если f(x) = a0xn + a1xn-1 + … + an-1x + an, g(x) =
- 19. Пример 1 x4 – 3 x3 – 3x2 + 11x – 6 Решение. По схеме Горнера
- 21. Скачать презентацию









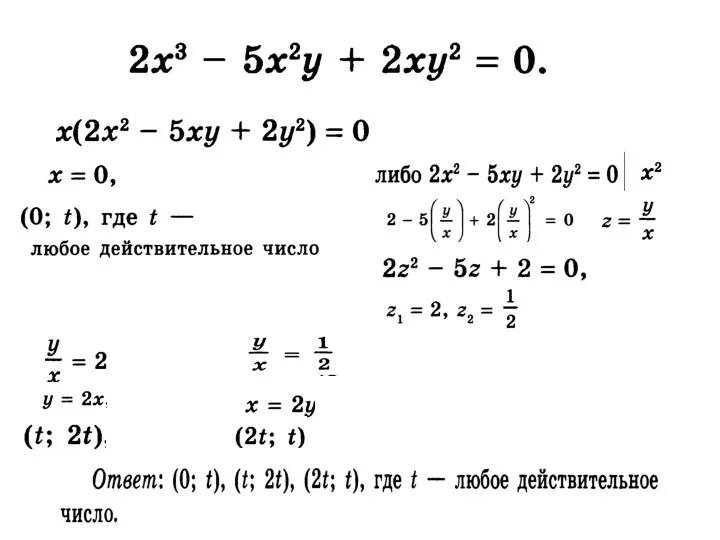








 Золотий переріз
Золотий переріз Пропорция
Пропорция Комбинаторика. Комбинаторные задачи
Комбинаторика. Комбинаторные задачи Презентация Состав числа 8
Презентация Состав числа 8 Вписанные и описанные четырехугольники
Вписанные и описанные четырехугольники Конус. Предметы, имеющие коническую поверхность
Конус. Предметы, имеющие коническую поверхность Komarova_otchet
Komarova_otchet Свойства функций. Урок алгебры в 9 классе
Свойства функций. Урок алгебры в 9 классе Площадь параллелограмма, треугольника, трапеции
Площадь параллелограмма, треугольника, трапеции Шкалы и координаты
Шкалы и координаты Trigonometry. Angles add to 180°
Trigonometry. Angles add to 180° Понятие квадратного корня из неотрицательного числа
Понятие квадратного корня из неотрицательного числа Правильные многогранники. 10 класс
Правильные многогранники. 10 класс Кездейсоқ шамалар және олардың берілу тәсілдері
Кездейсоқ шамалар және олардың берілу тәсілдері Параллелограмм. Свойство параллелограмма
Параллелограмм. Свойство параллелограмма Рівняння х^2=a
Рівняння х^2=a Единицы измерения площади и объема
Единицы измерения площади и объема Повторим математику. Итоговое повторение курса 5 класса
Повторим математику. Итоговое повторение курса 5 класса Доба. Замкнені і незамкнені лінії. Повторення вивченого. Урок №28
Доба. Замкнені і незамкнені лінії. Повторення вивченого. Урок №28 Решение задач с помощью уравнений
Решение задач с помощью уравнений Урок занимательной математики по теме Обыкновенные дроби. 5 класс
Урок занимательной математики по теме Обыкновенные дроби. 5 класс Урок-игра Морской бой
Урок-игра Морской бой Основные понятия теории вероятностей
Основные понятия теории вероятностей урок-презентация 1класс
урок-презентация 1класс Нумерация чисел (от 1 до 1000)
Нумерация чисел (от 1 до 1000) Презентация к уроку математики и конструирования в 3 классе.
Презентация к уроку математики и конструирования в 3 классе. тренажёр Решаем задачи с Буратино
тренажёр Решаем задачи с Буратино Целые числа. Рациональные числа
Целые числа. Рациональные числа