Содержание
- 3. МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ 3sin2x – 5sinx – 2 = 0 2sin2x + 3cosx =
- 4. ответ: НЕ ИМЕЕТ РЕШЕНИЯ МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ
- 5. МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ
- 6. МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ НЕ ИМЕЕТ РЕШЕНИЯ ответ:
- 7. МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
- 8. ответ: МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
- 9. Уравнение вида аsinx + bcosx = 0 называют однородным тригонометрическим уравнением первой степени. ОПРЕДЕЛЕНИЕ: Алгоритм решения
- 10. ОПРЕДЕЛЕНИЕ: Уравнение вида a sin2x + b sinx cosx + c cos²x = 0 называют однородным
- 11. Алгоритм решения однородного тригонометрического уравнения второй степени: Посмотреть, есть ли в уравнении член asin2 x. Если
- 12. ОДНОРОДНЫЕ УРАВНЕНИЯ 5sinx + 6cosx = 0 3sin2x +sinxсosx =2cos2x
- 13. ОДНОРОДНЫЕ УРАВНЕНИЯ ответ:
- 14. ОДНОРОДНЫЕ УРАВНЕНИЯ
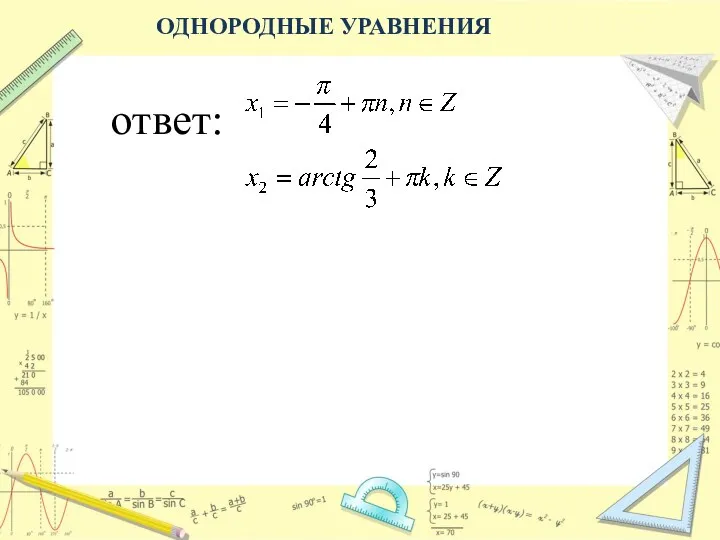
- 15. ОДНОРОДНЫЕ УРАВНЕНИЯ ответ:
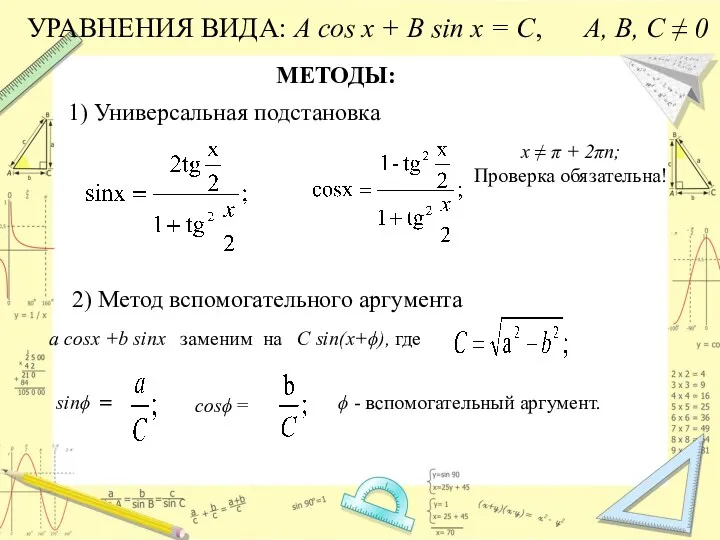
- 16. УРАВНЕНИЯ ВИДА: А cos x + B sin x = C, А, В, С ≠ 0
- 17. САМОСТОЯТЕЛЬНАЯ РАБОТА Вариант 1 На «3» 1) 3 sin x+ 5 cos x = 0 2)
- 19. Скачать презентацию














 Конспект урока по теме: Систематизация и обобщение знаний по теме Числа от 1 до 20, 1 класс
Конспект урока по теме: Систематизация и обобщение знаний по теме Числа от 1 до 20, 1 класс Эффективность подхода к обучению математики
Эффективность подхода к обучению математики Число 8, цифра 8. Диск
Число 8, цифра 8. Диск Нумерация. Счёт предметов. Разряды
Нумерация. Счёт предметов. Разряды Математические идеи в почвоведении. Методы статистического анализа данных. (Лекция 1)
Математические идеи в почвоведении. Методы статистического анализа данных. (Лекция 1) Предел последовательности
Предел последовательности Презентация Арифметический диктант
Презентация Арифметический диктант Производная и первообразная. Задание 7 ЕГЭ профильной математики
Производная и первообразная. Задание 7 ЕГЭ профильной математики Пифагор Самосский
Пифагор Самосский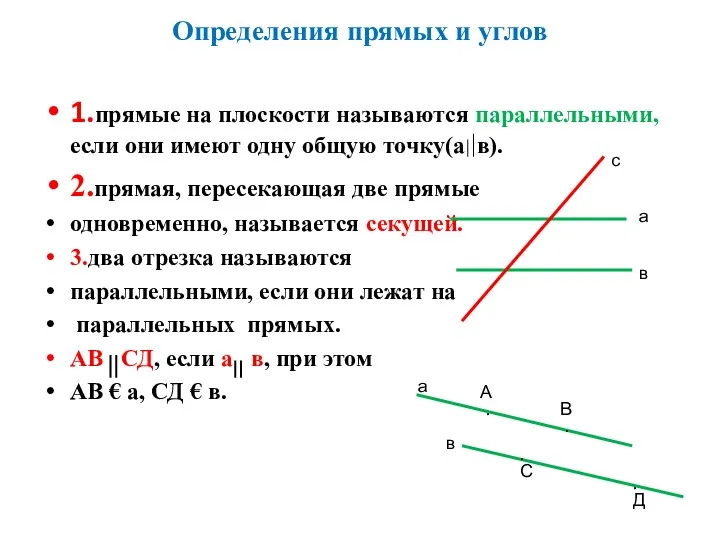 Определения прямых и углов
Определения прямых и углов Параллельные прямые
Параллельные прямые Задачи на проценты
Задачи на проценты Функції. Побудова графіків функції на площині
Функції. Побудова графіків функції на площині Цилиндр. Площадь поверхности цилиндра. Решение задач
Цилиндр. Площадь поверхности цилиндра. Решение задач Окружность. Радиус окружности
Окружность. Радиус окружности Презентация к уроку математике 3 класс УМК Школа России по теме Закрепление по таблице умножения и деления на 2,3,4.Таблица Пифагора.
Презентация к уроку математике 3 класс УМК Школа России по теме Закрепление по таблице умножения и деления на 2,3,4.Таблица Пифагора.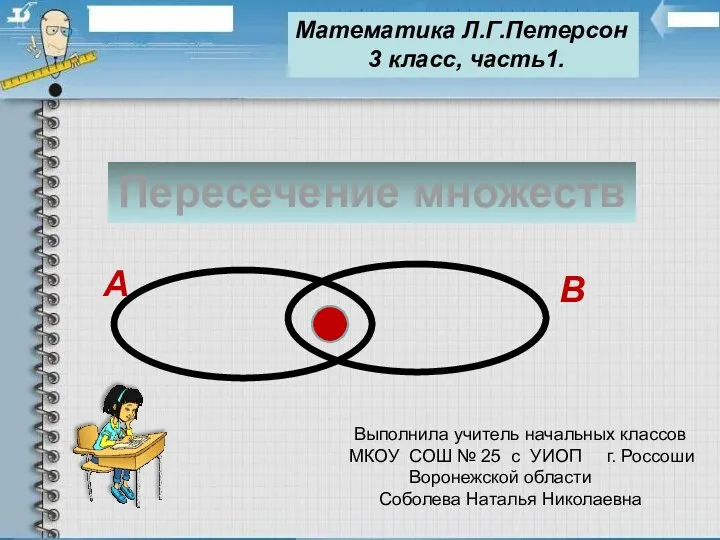 презентация по математике Пересечение множеств
презентация по математике Пересечение множеств Числовые наборы. Среднее арифметическое
Числовые наборы. Среднее арифметическое Прибавить число 6.
Прибавить число 6. Математические методы. Теория игр
Математические методы. Теория игр Стохастическая модель
Стохастическая модель Віднімання натуральних чисел. Властивості віднімання
Віднімання натуральних чисел. Властивості віднімання Функция ұғымы және оның берілу тәсілдері
Функция ұғымы және оның берілу тәсілдері Возникновение и развитие алгебры
Возникновение и развитие алгебры Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Деление и дроби. Представление натуральных чисел дробями
Деление и дроби. Представление натуральных чисел дробями Закрепление пройденного:действия с нулем и единицей, случаи деления вида 7:7,7:1
Закрепление пройденного:действия с нулем и единицей, случаи деления вида 7:7,7:1 Урок математика 2 класс. Закрепление, решение задач.
Урок математика 2 класс. Закрепление, решение задач.