Содержание
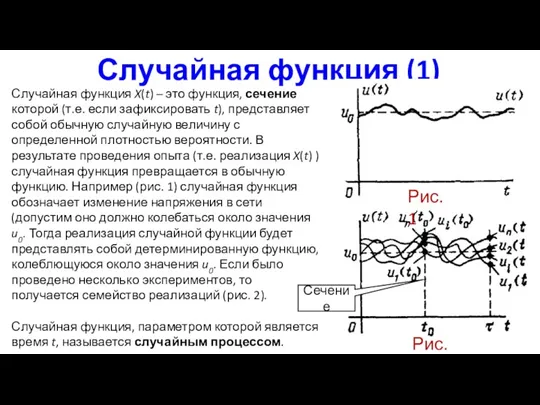
- 2. Случайная функция (1) Случайная функция X(t) – это функция, сечение которой (т.е. если зафиксировать t), представляет
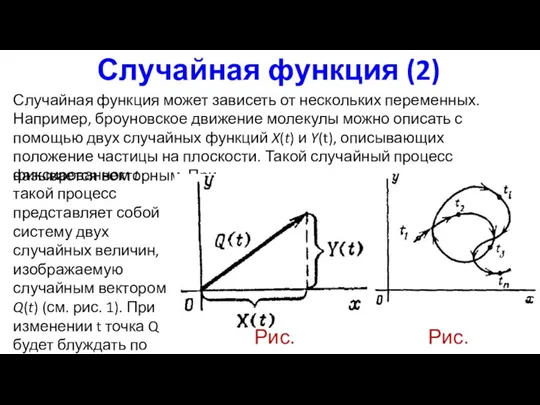
- 3. Случайная функция (2) Случайная функция может зависеть от нескольких переменных. Например, броуновское движение молекулы можно описать
- 4. Случайная функция (3) Многомерный случайный процесс – когда существует множество описываемых случайным процессом параметров. Например, полет
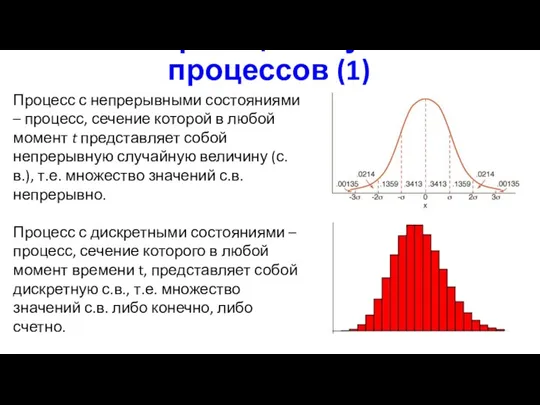
- 5. Классификация случайных процессов (1) Процесс с непрерывными состояниями – процесс, сечение которой в любой момент t
- 6. Классификация случайных процессов (2) Процесс с непрерывным временем – процесс, при котором объект может изменять состояние
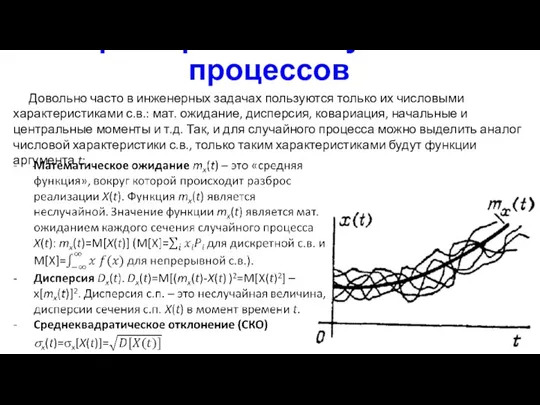
- 7. Характеристики случайных процессов Довольно часто в инженерных задачах пользуются только их числовыми характеристиками с.в.: мат. ожидание,
- 8. Теория случайных процессов (функций) Р-схема моделирует случайный процесс Случайный процесс X(t) – это функция, которая в
- 9. Примеры случайных процессов Случайны автомат (на дугах этого автомата стоят вероятности перехода из одного состояния в
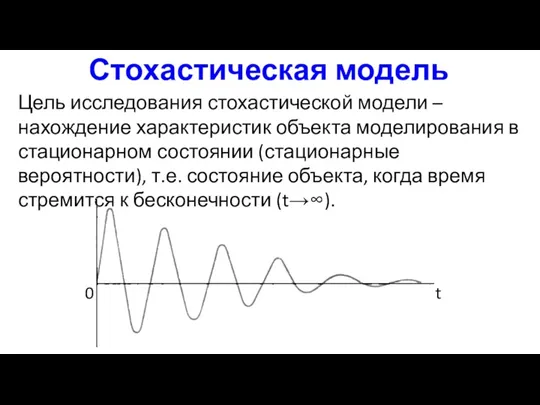
- 10. Стохастическая модель Цель исследования стохастической модели – нахождение характеристик объекта моделирования в стационарном состоянии (стационарные вероятности),
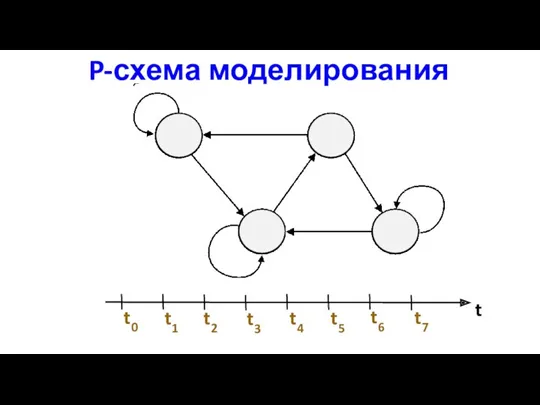
- 11. P-схема моделирования t t0 t1 t2 t3 t4 t5 t6 t7
- 12. А.А. Марков (старший) – основоположник теории сетей Маркова А.А. Марков (1856 - 1922) Оставил труды в
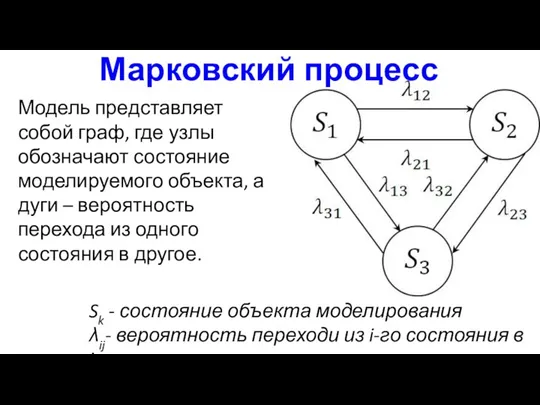
- 13. Модель представляет собой граф, где узлы обозначают состояние моделируемого объекта, а дуги – вероятность перехода из
- 14. Марковские процессы Марковские процессы делятся на два вида: Дискретные (цепи Маркова), где система меняет свое состояние
- 15. Свойство марковости
- 16. Условная вероятность Условной называется вероятность, что произойдет какое-либо событие, если известно, что произошло до этого произошло
- 17. Примеры дискретных марковских процессов 1. Ветвящийся процесс Гальтона – Ватсона Наблюдается популяция живых организмов в дискретные
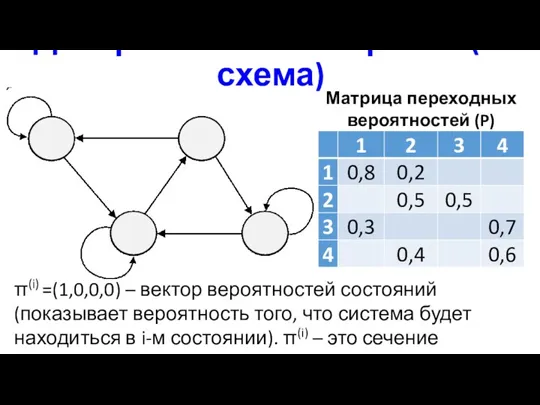
- 18. Дискретная сеть Маркова (P-схема) Матрица переходных вероятностей (P) π(i) =(1,0,0,0) – вектор вероятностей состояний (показывает вероятность
- 19. Матрица вероятностей перехода Сумма всех элементов в строке матрицы вероятностей равняется единице!!! =1 =1 =1 =1
- 20. Имитационное моделирование дискретной сети Маркова π(n)=π(n-1)*P (*), где n – номер шага моделирования. Моделирование представляет собой
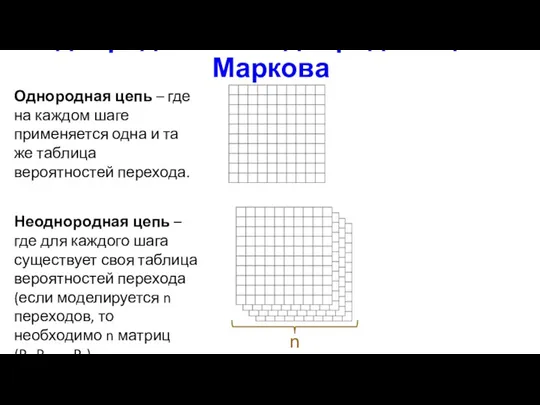
- 21. Однородная и неоднородная цепи Маркова Однородная цепь – где на каждом шаге применяется одна и та
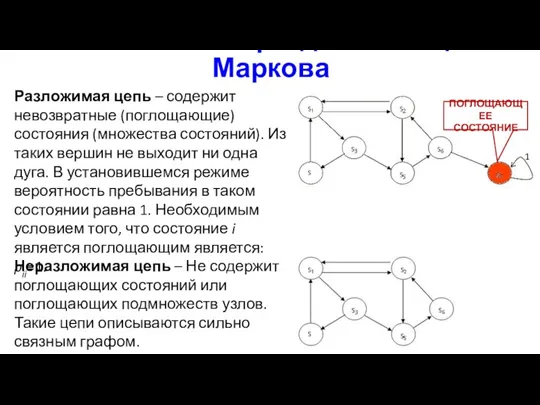
- 22. Разложимая и эргодическая цепи Маркова Разложимая цепь – содержит невозвратные (поглощающие) состояния (множества состояний). Из таких
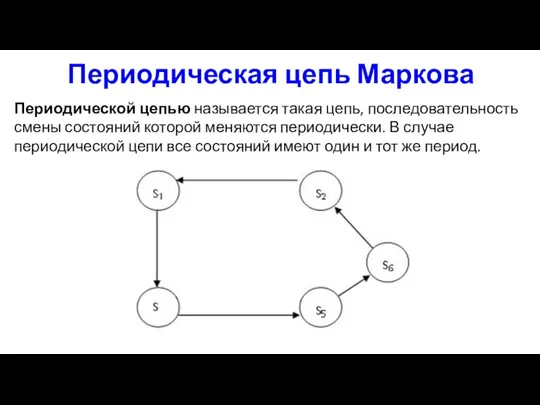
- 23. Периодическая цепь Маркова Периодической цепью называется такая цепь, последовательность смены состояний которой меняются периодически. В случае
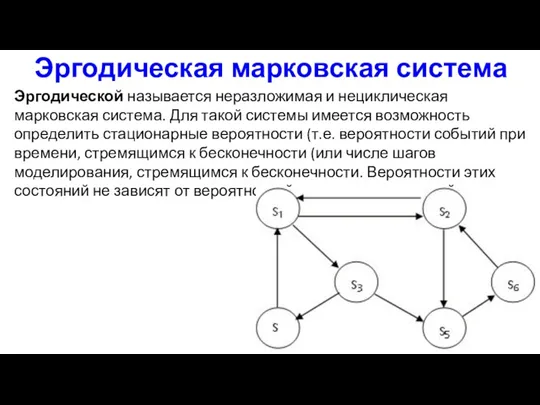
- 24. Эргодическая марковская система Эргодической называется неразложимая и нециклическая марковская система. Для такой системы имеется возможность определить
- 25. Теорема о существовании предельных вероятностей марковской цепи
- 26. Пример моделирования цепи Маркова (1) π =(1,0,0,0) – начальное состояние; 1 шаг: P’=(0.8, 0.2, 0, 0);
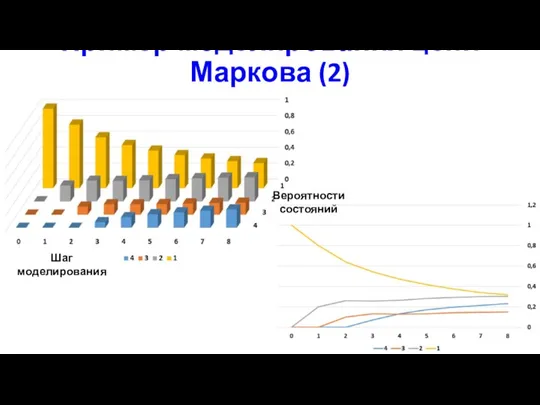
- 27. Пример моделирования цепи Маркова (2) Шаг моделирования Вероятности состояний
- 28. Пример моделирования цепи Маркова (2) π=(0.25, 0.25, 0.25, 0.25); 1 шаг: P’=(0.275, 0.275, 0.125, 0.325); ε=
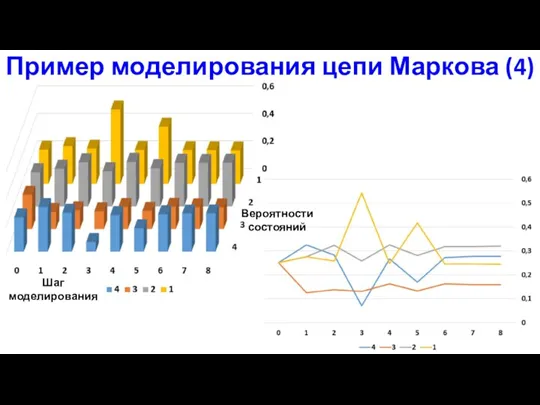
- 29. Пример моделирования цепи Маркова (4) Шаг моделирования Вероятности состояний
- 30. Аналитическое моделирование цепи Маркова
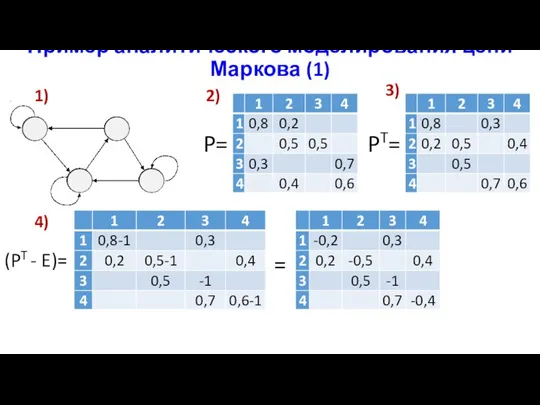
- 31. Пример аналитического моделирования цепи Маркова (1) P= PT= 1) 2) 3) 4) (PT - E)= =
- 32. Пример аналитического моделирования цепи Маркова (2) 5) Решим линейную систему уравнений (PT - E)=(0,0,…,0,1)T = 6)
- 33. Пример аналитического моделирования цепи Маркова (2) 5) Решим линейную систему уравнений (PT - E)=(0,0,…,0,1)T = 6)
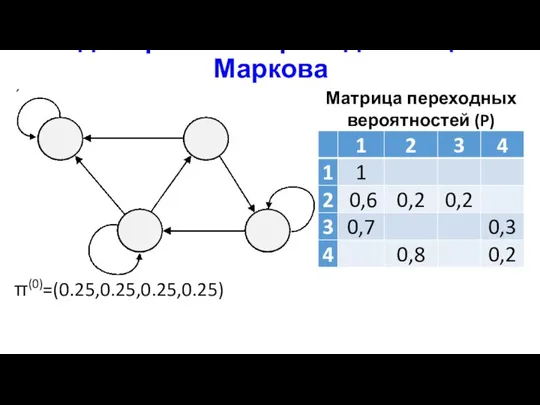
- 34. Моделирование приводимой цепи Маркова Матрица переходных вероятностей (P) π(0)=(0.25,0.25,0.25,0.25)
- 35. Пример моделирования приводимой цепи Маркова π =(0.25,0.25,0.25,0.25) – начальное состояние; 1 шаг: P’=(0.575 0.25 0.05 0.125);
- 36. Методика моделирования по схеме дискретных марковских процессов Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских
- 38. Скачать презентацию



















 Математические методы в педагогике
Математические методы в педагогике Случайный опыт и случайное событие. Вероятность события. 7 класс
Случайный опыт и случайное событие. Вероятность события. 7 класс Умножение разности двух выражений на их сумму
Умножение разности двух выражений на их сумму Порядок выполнения действий. Скобки. 3 класс.
Порядок выполнения действий. Скобки. 3 класс. Анализ временных рядов экономических процессов. Лекция 3
Анализ временных рядов экономических процессов. Лекция 3 .Презентация по теме Площадь геометрической фигуры
.Презентация по теме Площадь геометрической фигуры Сложение и вычитание смешанных чисел. 5 класс
Сложение и вычитание смешанных чисел. 5 класс Транспортная задача
Транспортная задача КВМ. Задачи. 6 класс
КВМ. Задачи. 6 класс Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса
Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса Вписанные и описанные окружности
Вписанные и описанные окружности Умножение числа 10
Умножение числа 10 Решение задач, масса одного предмета, количество, масса всех предметов
Решение задач, масса одного предмета, количество, масса всех предметов Порівняння чисел в межах 8
Порівняння чисел в межах 8 Урок математики в 3 классе по теме Внетабличное умножение и деление
Урок математики в 3 классе по теме Внетабличное умножение и деление Повторение знаний о нумерации. Числа от 11 до 20
Повторение знаний о нумерации. Числа от 11 до 20 Карл Фридрих Гаусс
Карл Фридрих Гаусс Урок математики. Запись чисел римскими цифрами
Урок математики. Запись чисел римскими цифрами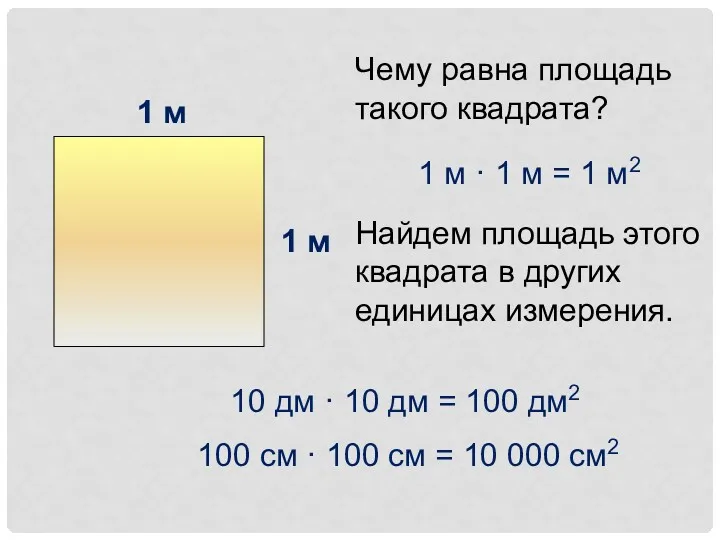 Площадь квадрата
Площадь квадрата Письменное умножение на числа, оканчивающиеся нулями
Письменное умножение на числа, оканчивающиеся нулями Задачи на смекалку
Задачи на смекалку Конус. Означення та елементи конуса. Перерізи конуса. (11 клас)
Конус. Означення та елементи конуса. Перерізи конуса. (11 клас) Решение системы уравнений способом подстановки
Решение системы уравнений способом подстановки Координаты на прямой. 6 класс
Координаты на прямой. 6 класс Способы проецирования
Способы проецирования Пропорции и отношения. Отношения. Основное свойство отношений
Пропорции и отношения. Отношения. Основное свойство отношений Решение систем уравнений с двумя неизвестными
Решение систем уравнений с двумя неизвестными Задачи повышенной сложности.
Задачи повышенной сложности.