Содержание
- 2. Трёхгранные и многогранные углы: Трёхгранным углом называется фигура образованная тремя плоскостями, ограни- ченными тремя лучами, исходящими
- 3. Трёхгранный угол — это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими
- 4. Основные свойства трехгранного угла 1. Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских
- 5. , 5. Теорема синусов Многогранный угол, внутренняя область которого расположена по одну сторону от плоскости каждой
- 6. Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.
- 7. Грани многогранника - это многоугольники, которые его образуют. Ребра многогранника - это стороны многоугольников. Вершины многогранника
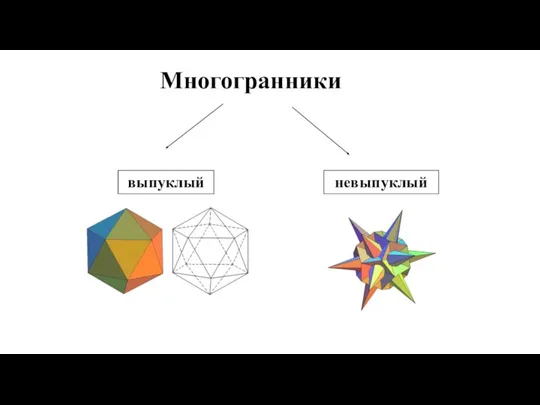
- 8. выпуклый невыпуклый Многогранники
- 9. Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности.
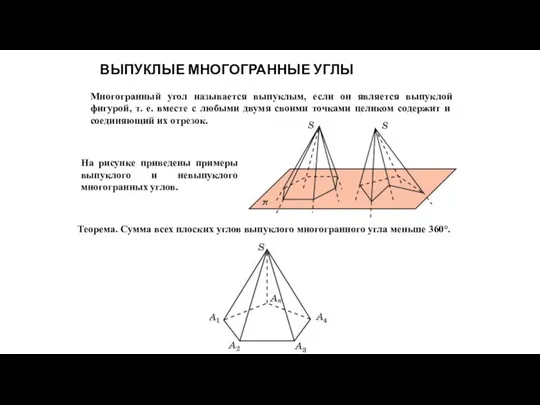
- 10. ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫ Многогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с
- 11. ВЫПУКЛЫЕ МНОГОГРАННИКИ Многогранник угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми
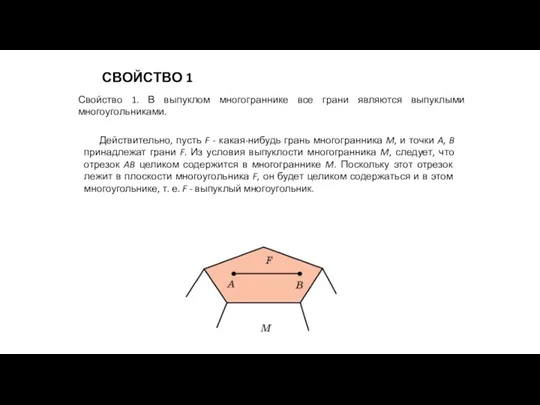
- 12. СВОЙСТВО 1 Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками. Действительно, пусть F -
- 13. СВОЙСТВО 2 Действительно, пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника M, т.
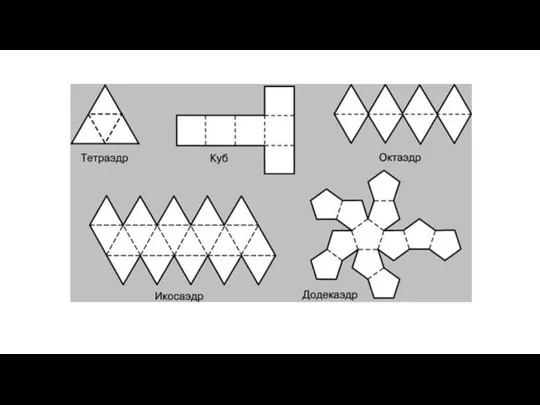
- 14. Правильные многогранники Если грани многогранника являются правильными многоугольниками с одним и тем же числом сторон и
- 15. пришли из Древней Греции, в них указывается число граней: «эдра» − грань; «тетра» − 4; «гекса»
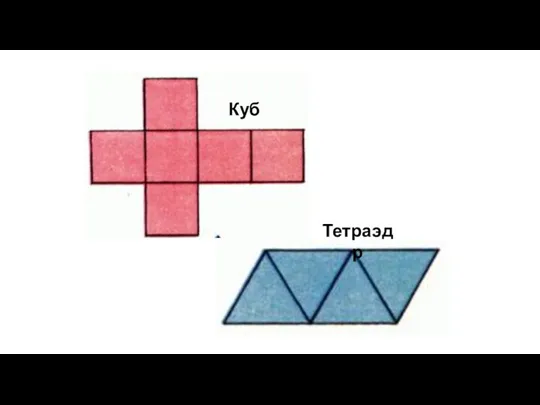
- 16. Правильный тетраэдр Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма
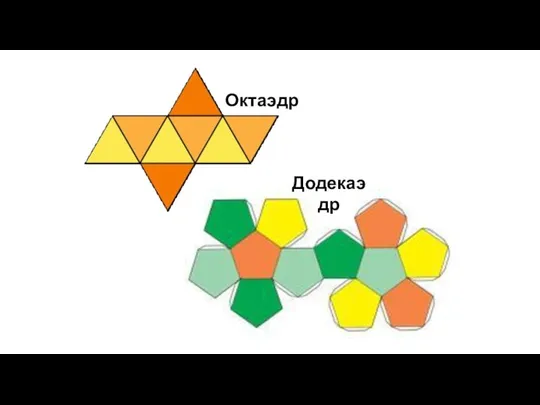
- 17. Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов
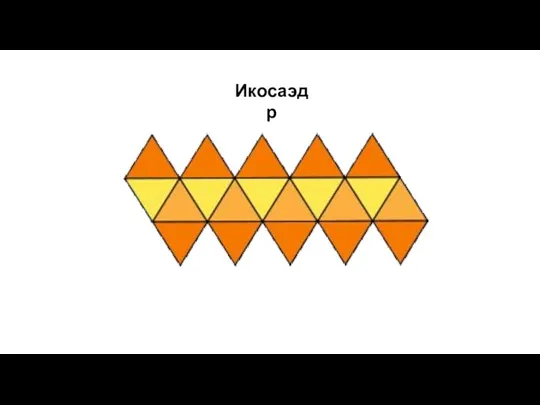
- 18. Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма
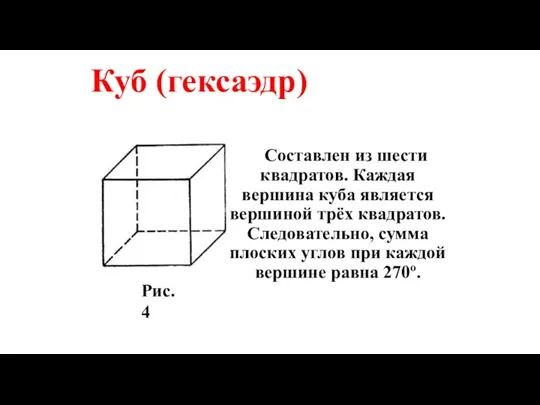
- 19. Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при
- 20. Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно,
- 21. Таблица № 1
- 22. Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В
- 23. Таблица № 2
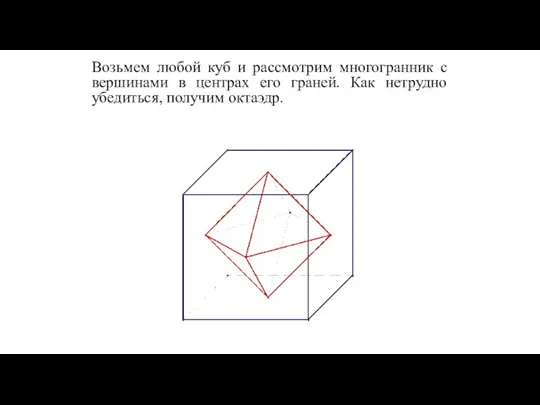
- 26. Двойственность правильных многогранников Гексаэдр (куб) и октаэдр образуют двойственную пару многогранников. Число граней одного многогранника равно
- 27. Возьмем любой куб и рассмотрим многогранник с вершинами в центрах его граней. Как нетрудно убедиться, получим
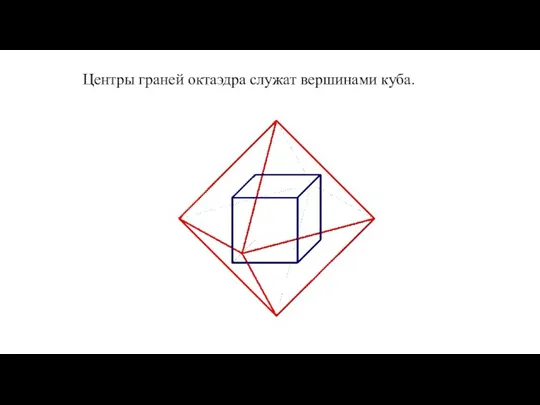
- 28. Центры граней октаэдра служат вершинами куба.
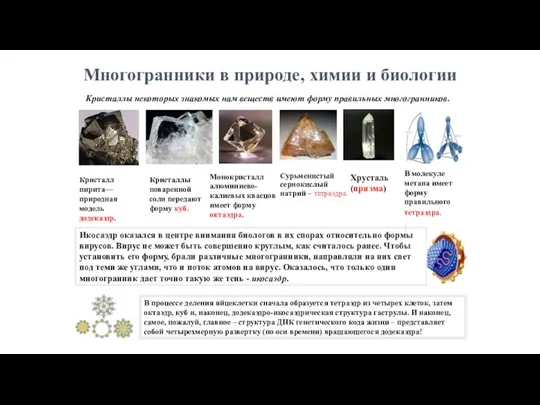
- 29. Сурьменистый сернокислый натрий – тетраэдра. Многогранники в природе, химии и биологии Кристаллы некоторых знакомых нам веществ
- 30. Многогранники в искусстве «Портрет Монны Лизы» Композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого
- 31. Многогранники в архитектуре Музеи Плодов в Яманаши создан с помощью трехмерного моделирования. Четырехъярусная Спасская башня с
- 34. ПРИЗМА
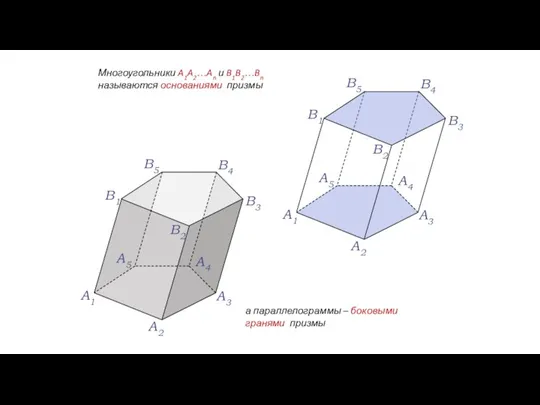
- 35. Понятие призмы Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и
- 36. Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы а параллелограммы – боковыми гранями призмы A1 A2 A3
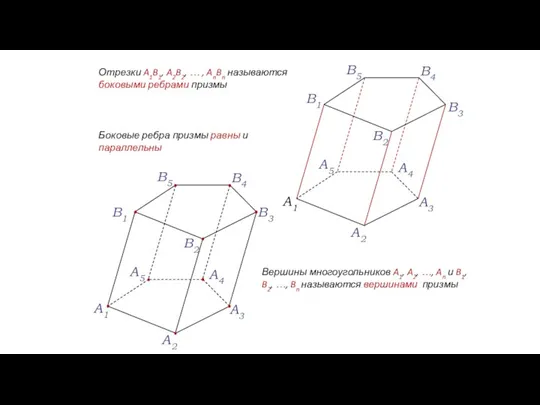
- 37. Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы Боковые ребра призмы равны и параллельны
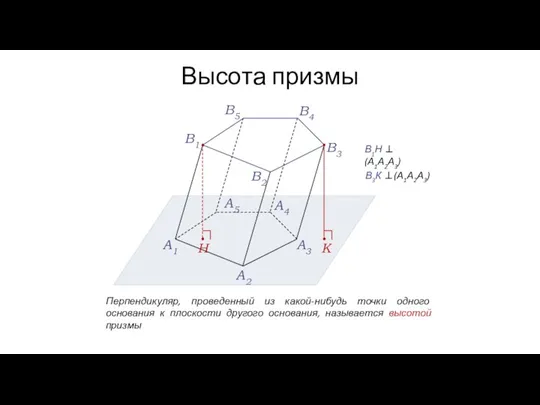
- 38. Высота призмы A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 К Н Перпендикуляр, проведенный
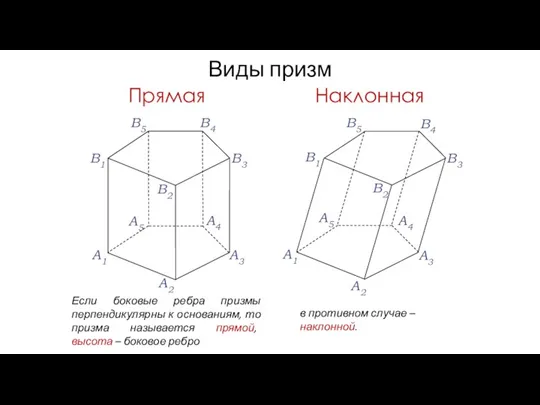
- 39. Виды призм A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Если боковые ребра призмы
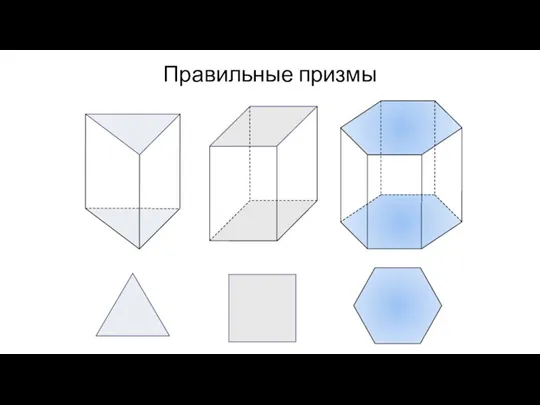
- 40. Правильная призма A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Прямая призма называется правильной,
- 41. Правильные призмы
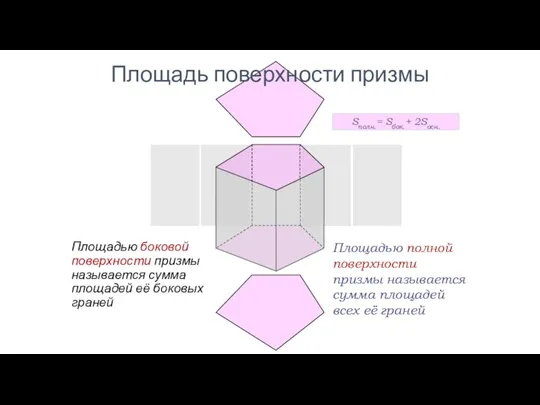
- 42. Площадью боковой поверхности призмы называется сумма площадей её боковых граней Площадью полной поверхности призмы называется сумма
- 43. Теорема о площади боковой поверхности прямой призмы Площадь боковой поверхности прямой призмы равна произведению периметра основания
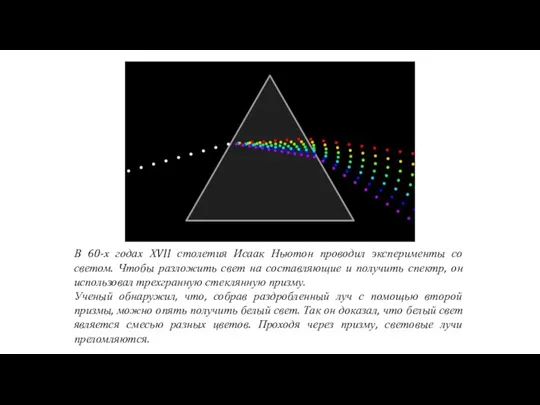
- 44. В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет на составляющие
- 45. «Я затемнил мою комнату, − писал он, − и сделал очень маленькое отверстие в ставне для
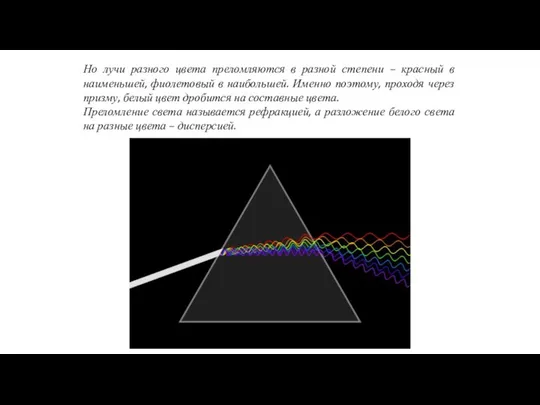
- 46. Но лучи разного цвета преломляются в разной степени – красный в наименьшей, фиолетовый в наибольшей. Именно
- 47. Использование призмы для творческих фотоэффектов
- 48. Архитектура, оптика, медицина, электронная техника. (очки, бинокли, объективы, телефоны)
- 49. Применение призм в лечении косоглазия Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное
- 50. Определение Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и
- 51. Свойства
- 52. Виды параллелограмма Прямоугольный параллелепипед ( многогранник с шестью гранями, каждая из которых является в общем случае
- 53. S полн 2(ab+bc+ac) = V = abc Объем прямоугольного параллелепипеда Поверхность прямоугольного параллелепипеда
- 54. Куб ( правильный многогранник, каждая грань которого представляет собой квадрат.) Площадь поверхности S=6a2 Объём V=a3
- 55. Прямой параллелепипед (это параллелепипед, у которого 4 боковые грани прямоугольники.)
- 56. Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота Площадь полной поверхности Sп=Sб+2Sо,
- 57. 3. Наклонный параллелепипед (это параллелепипед, боковые грани которого не перпендикулярны основаниям.)
- 58. Боковая поверхность Sбок.=Pосн.∙Н Полная поверхность Sполн.=2Sосн.+Sбок. Объем прямого параллелепипеда V=Sосн.∙Н
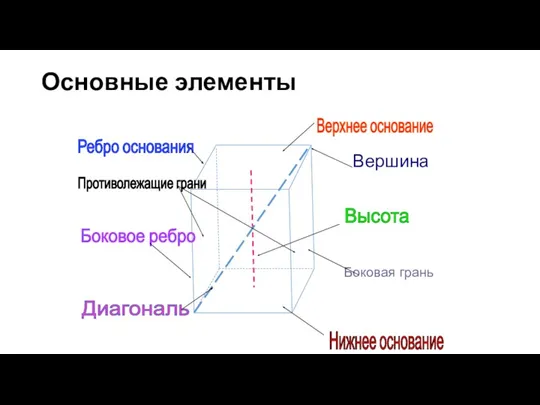
- 59. Основные элементы Верхнее основание Нижнее основание Высота Боковая грань Вершина Ребро основания Боковое ребро Диагональ Противолежащие
- 60. Параллелепипед в жизни человека
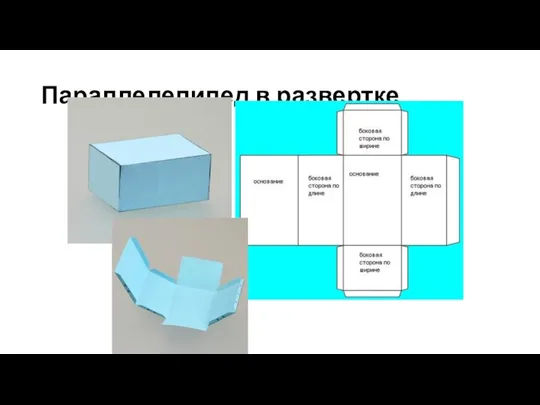
- 61. Параллелепипед в развертке
- 64. Пирамида Её элементы. Правильная пирамида. Усечённая пирамида
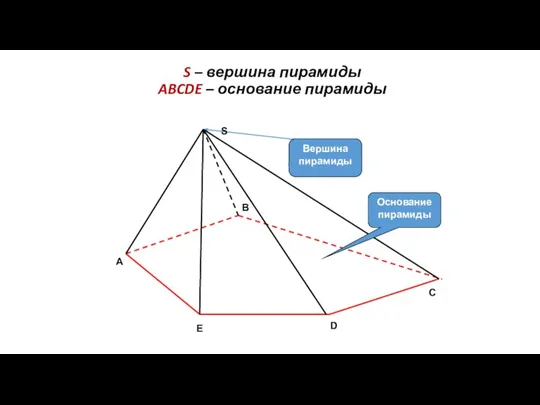
- 65. S – вершина пирамиды ABCDE – основание пирамиды C Основание пирамиды Вершина пирамиды
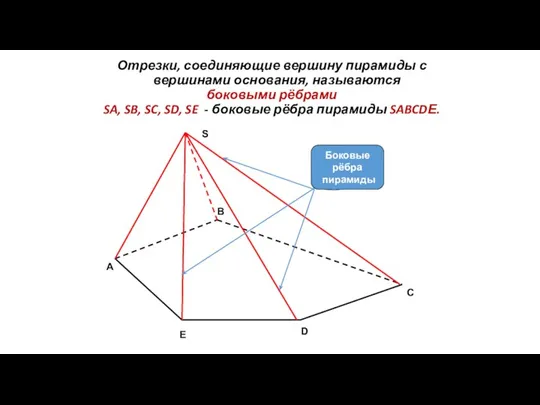
- 66. C Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами SA, SB, SC, SD, SE
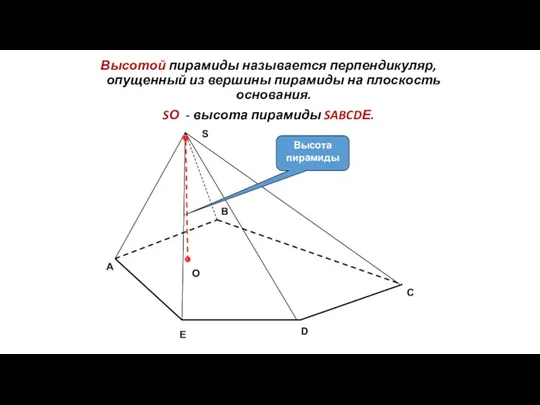
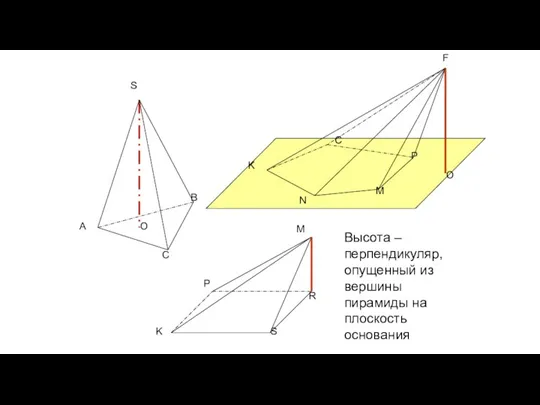
- 67. C Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. SО - высота пирамиды
- 68. O O Высота – перпендикуляр, опущенный из вершины пирамиды на плоскость основания
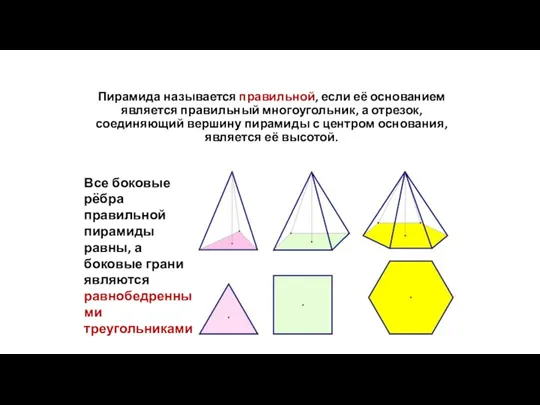
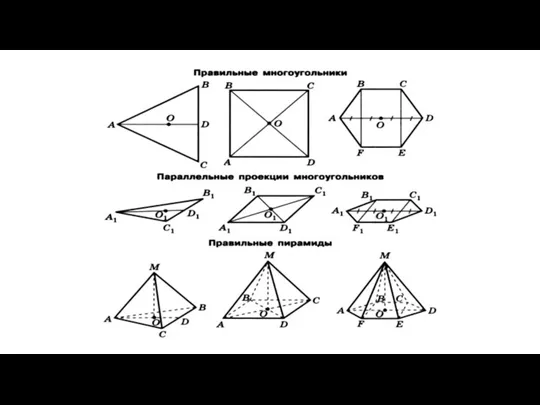
- 69. Пирамида называется правильной, если её основанием является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром
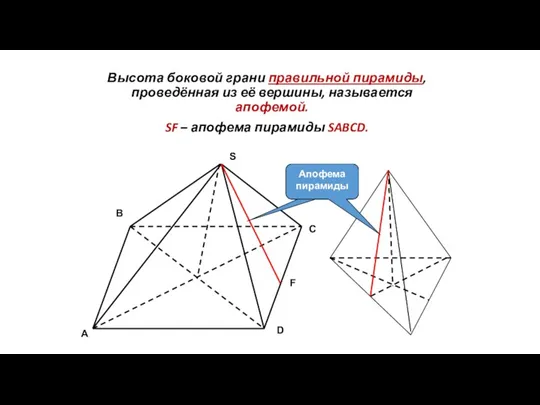
- 71. Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой. SF – апофема пирамиды SABCD.
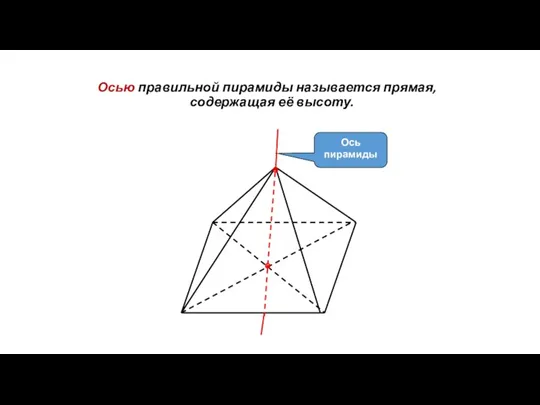
- 72. Осью правильной пирамиды называется прямая, содержащая её высоту. Ось пирамиды
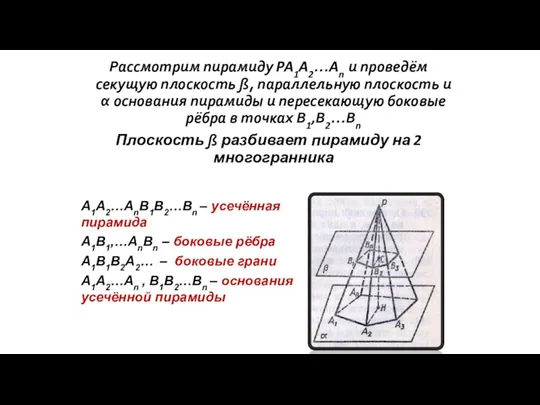
- 73. Рассмотрим пирамиду PA1A2…An и проведём секущую плоскость ß, параллельную плоскость и α основания пирамиды и пересекающую
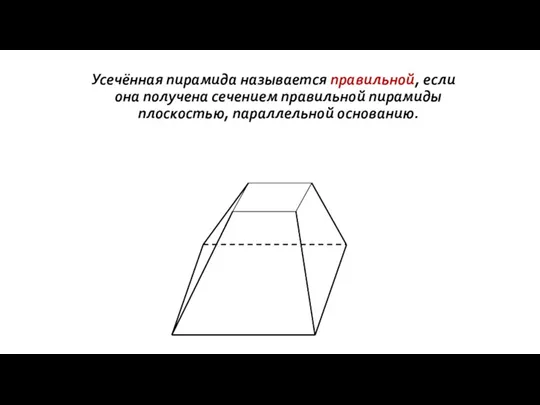
- 74. Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
- 75. Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания: Боковой поверхностью пирамиды называется
- 76. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему: p – периметр основания l
- 77. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему: p1 и p2
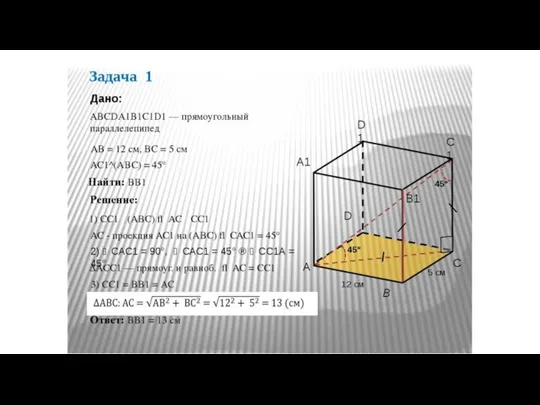
- 78. B Задача № 244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенуза AB=29 см,
- 79. ? 6 Задача №259. В правильной четырёхугольной пирамиде сторона основания равна 6 см, а угол наклона
- 80. Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом
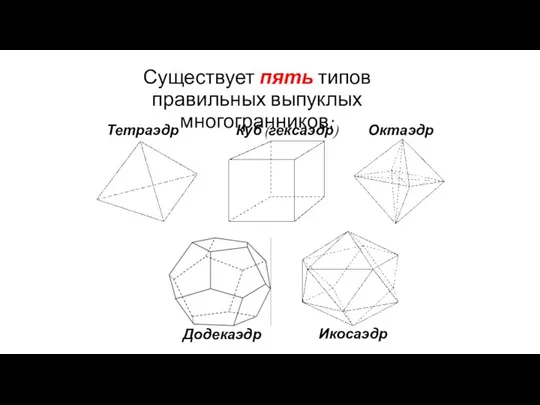
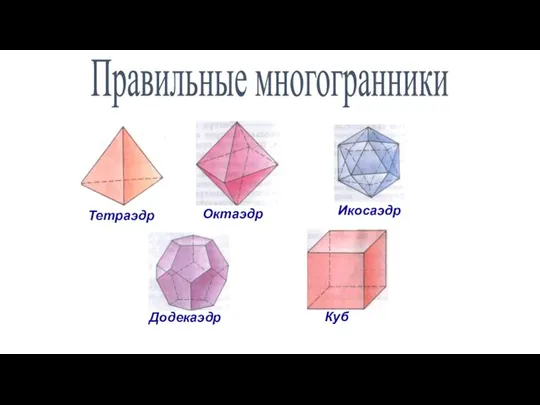
- 81. Существует пять типов правильных выпуклых многогранников:
- 82. Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n≥ 6.
- 83. Доказательство: Угол правильного n-угольника при n≥6 не меньше 120 градусов. С другой стороны, при каждой вершине
- 84. Доказательство: Значит, если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n≥6, то
- 85. Доказательство: Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше
- 86. Названия правильных многогранников пришли из Греции. Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их еще
- 87. Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы
- 88. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени. Икосаэдр - как самый
- 89. В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и
- 90. Правильный тетраэдр - это правильная треугольная пирамида, у которой все грани являются равносторонними треугольниками. Следовательно, сумма
- 91. Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов
- 92. Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма
- 93. Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно,
- 94. Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма
- 95. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В ПРИРОДЕ
- 96. Поваренная соль состоит из кристаллов в форме куба
- 97. Минерал сильвин также имеет кристаллическую решетку в форме куба.
- 98. Скелет одноклеточного организма феодарии представляет собой икосаэдр.
- 99. Кристаллы пирита имеют форму додекаэдра.
- 100. Минерал куприт образует кристаллы в форме октаэдров
- 101. Молекулы воды имеют форму тетраэдра
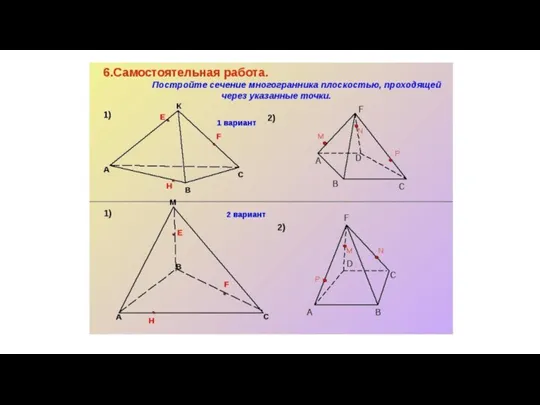
- 102. САМОСТОЯТЕЛЬНАЯ РАБОТА
- 103. Задание: Перерисуйте развертки правильных многогранников на плотные листы бумаги в большем масштабе, вырежьте развертки (сделав необходимые
- 104. Куб Тетраэдр
- 105. Додекаэдр Октаэдр
- 106. Икосаэдр
- 107. Сечения куба, призмы и пирамиды
- 109. Содержанием работы является построение сечений по точкам, заданным на рёбрах многогранников: 2. Пирамиды 3. Призмы 1.
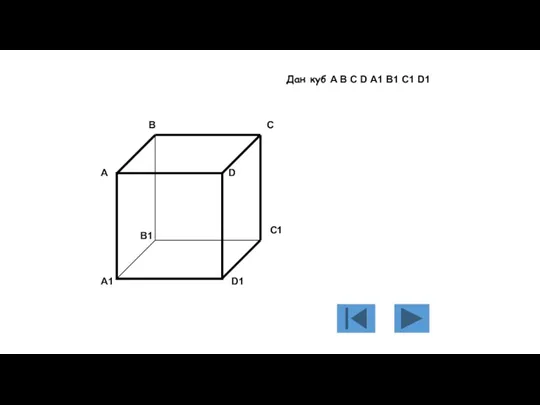
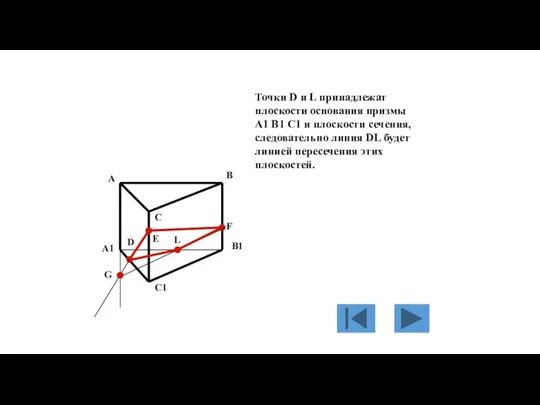
- 110. А В С D A1 B1 C1 D1 Дан куб A B C D A1 B1
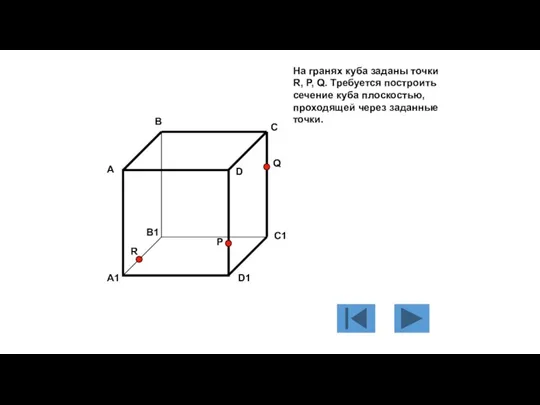
- 111. На гранях куба заданы точки R, P, Q. Требуется построить сечение куба плоскостью, проходящей через заданные
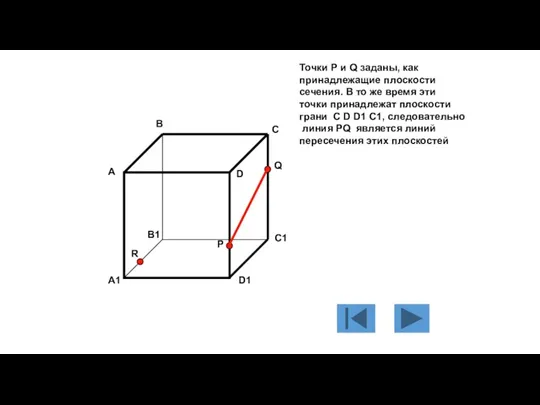
- 112. Точки Р и Q заданы, как принадлежащие плоскости сечения. В то же время эти точки принадлежат
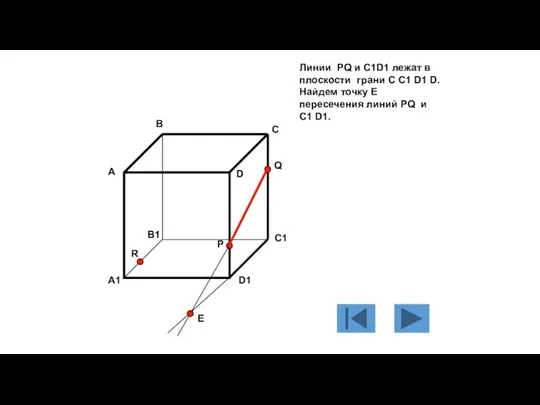
- 113. Линии PQ и C1D1 лежат в плоскости грани C C1 D1 D. Найдем точку Е пересечения
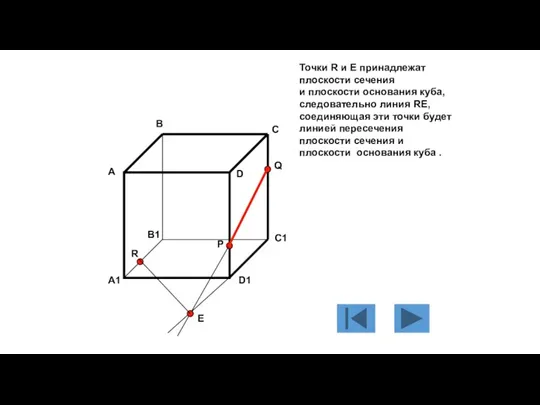
- 114. Точки R и E принадлежат плоскости сечения и плоскости основания куба, следовательно линия RE, соединяющая эти
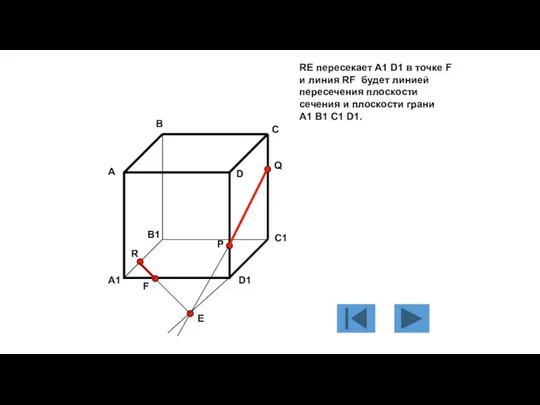
- 115. RE пересекает A1 D1 в точке F и линия RF будет линией пересечения плоскости сечения и
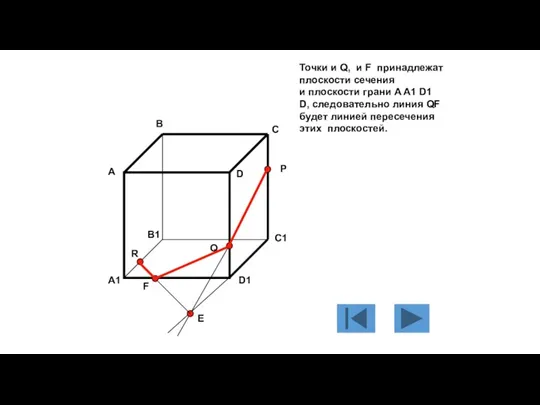
- 116. Точки и Q, и F принадлежат плоскости сечения и плоскости грани A A1 D1 D, следовательно
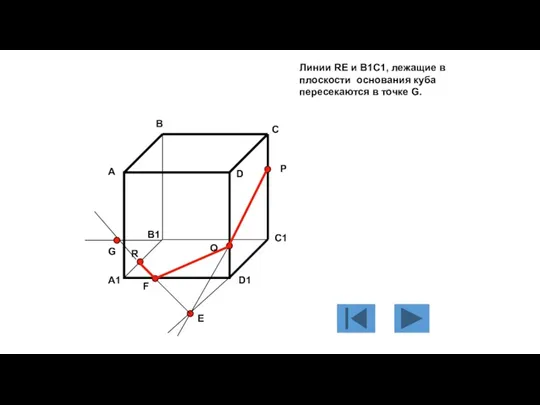
- 117. Линии RE и B1C1, лежащие в плоскости основания куба пересекаются в точке G. А В С
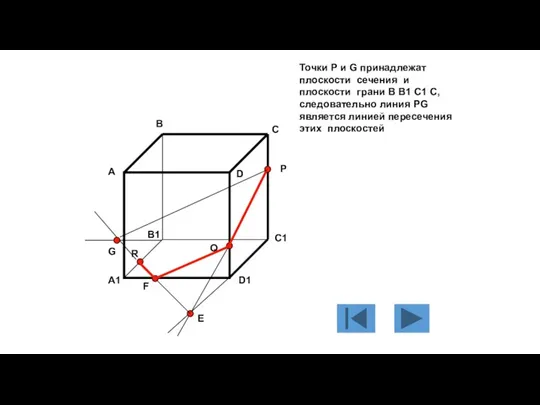
- 118. Точки P и G принадлежат плоскости сечения и плоскости грани B B1 C1 C, следовательно линия
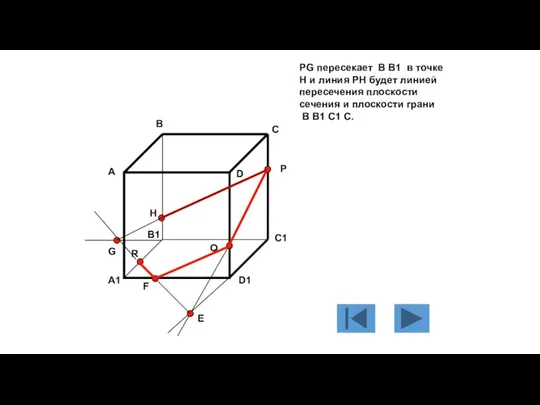
- 119. PG пересекает B B1 в точке H и линия PH будет линией пересечения плоскости сечения и
- 120. Точки R и H принадлежат плоскости сечения и плоскости грани A A1 B1 B и следовательно
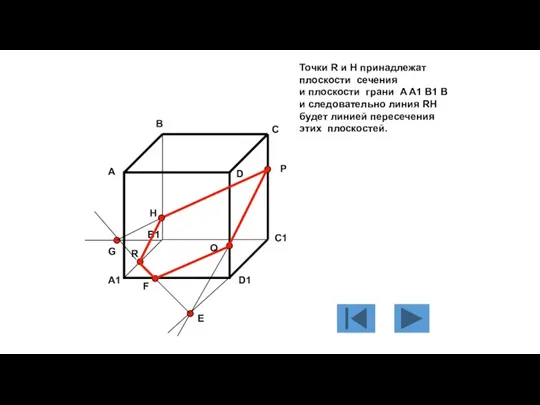
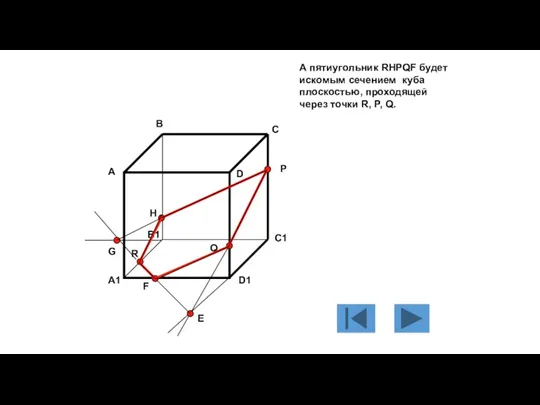
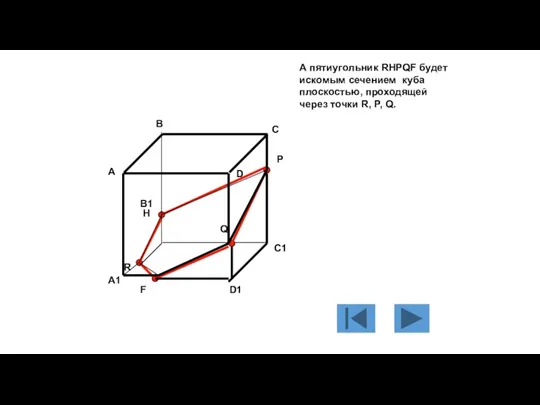
- 121. А пятиугольник RHPQF будет искомым сечением куба плоскостью, проходящей через точки R, P, Q. А В
- 122. А пятиугольник RHPQF будет искомым сечением куба плоскостью, проходящей через точки R, P, Q. А В
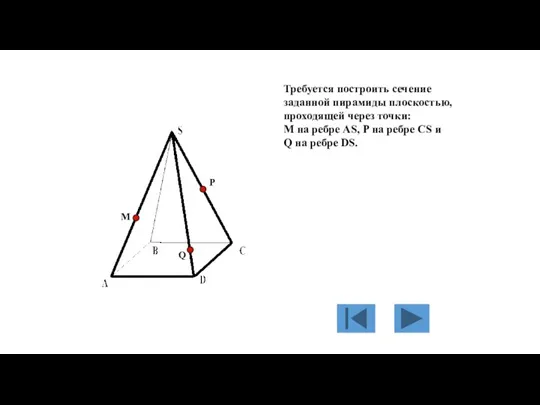
- 123. Дана пирамида SABCD.
- 124. Требуется построить сечение заданной пирамиды плоскостью, проходящей через точки: М на ребре AS, P на ребре
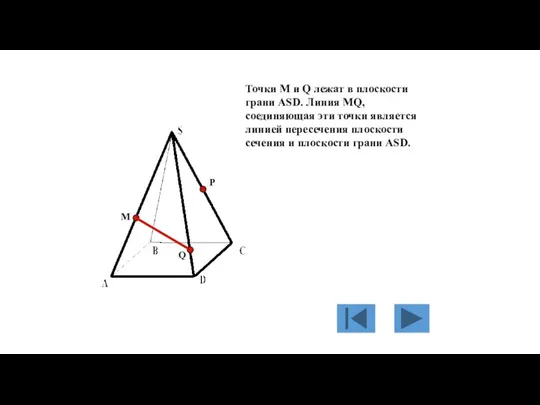
- 125. M P Q Точки M и Q лежат в плоскости грани АSD. Линия МQ, соединяющая эти
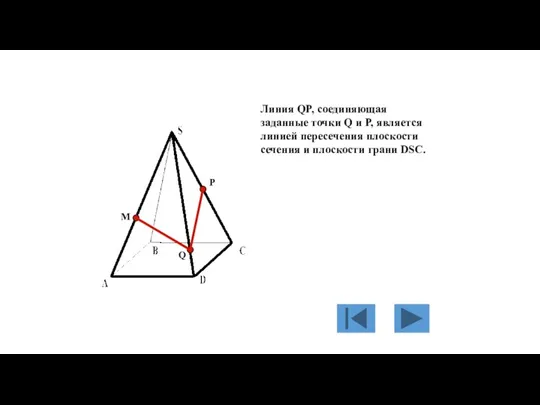
- 126. M P Q Линия QP, соединяющая заданные точки Q и P, является линией пересечения плоскости сечения
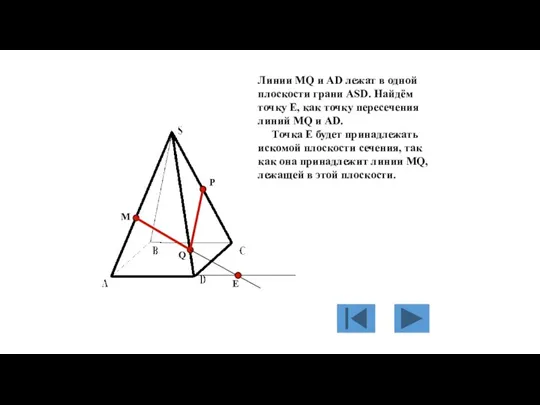
- 127. M P Q Линии MQ и AD лежат в одной плоскости грани ASD. Найдём точку Е,
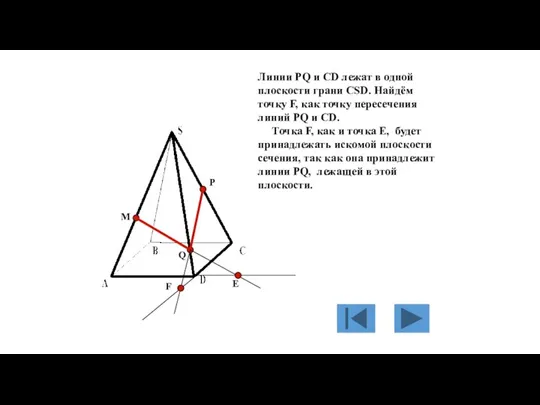
- 128. M P Q Е Линии PQ и CD лежат в одной плоскости грани CSD. Найдём точку
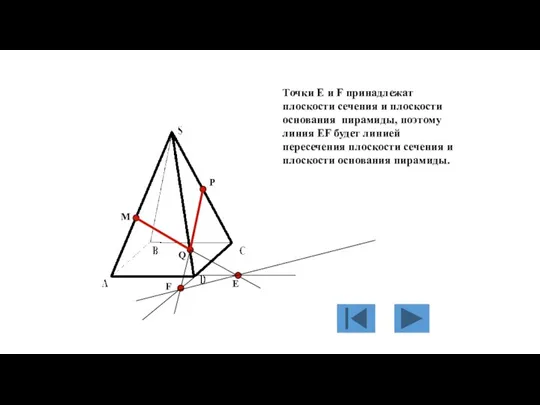
- 129. M P Q Е F Точки Е и F принадлежат плоскости сечения и плоскости основания пирамиды,
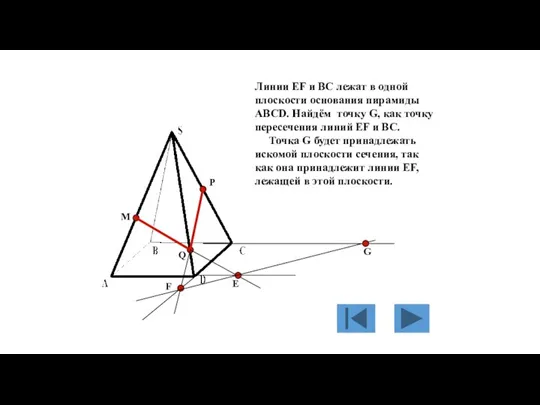
- 130. M P Q Е F Линии EF и BC лежат в одной плоскости основания пирамиды ABCD.
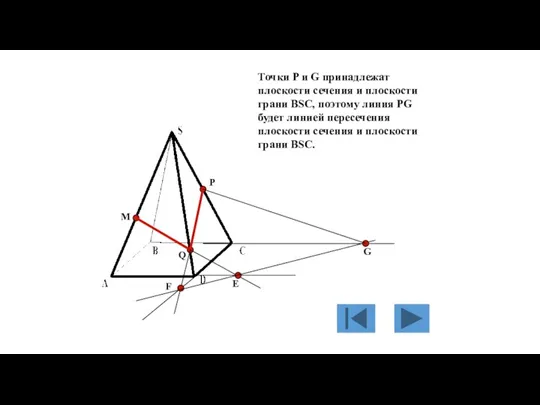
- 131. M P Q Е F G Точки P и G принадлежат плоскости сечения и плоскости грани
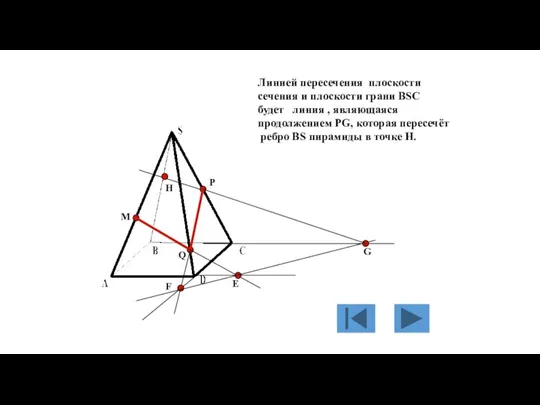
- 132. M P Q Е F G Линией пересечения плоскости сечения и плоскости грани BSC будет линия
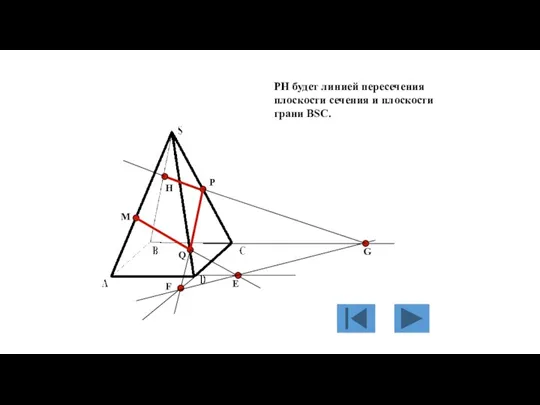
- 133. M P Q Е F G H PH будет линией пересечения плоскости сечения и плоскости грани
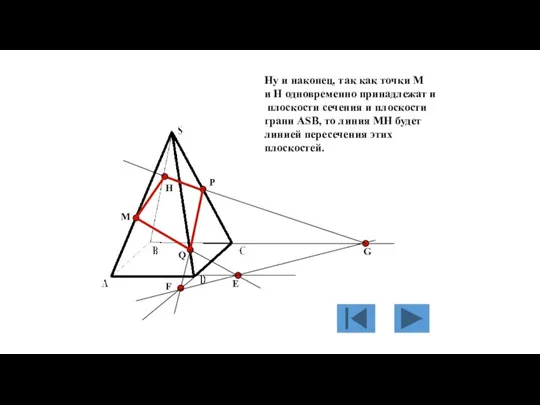
- 134. M P Q Е F G H Ну и наконец, так как точки M и H
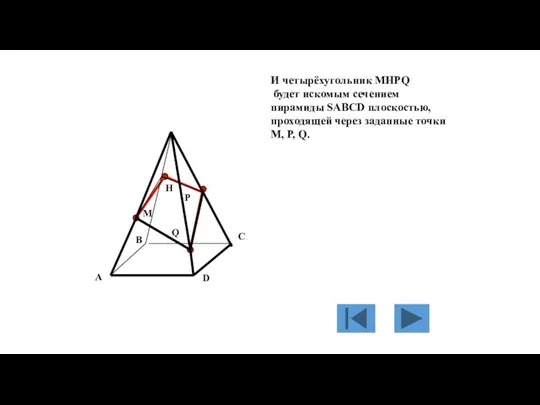
- 135. M P Q H И четырёхугольник MHPQ будет искомым сечением пирамиды SABCD плоскостью, проходящей через заданные
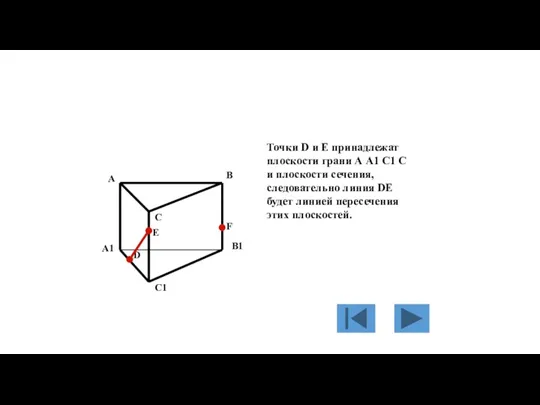
- 136. Дана трёхгранная призма A B C A1 B1 C1. Требуется построить сечение призмы плоскостью, проходящей через
- 137. Точки D и E принадлежат плоскости грани А А1 С1 С и плоскости сечения, следовательно линия
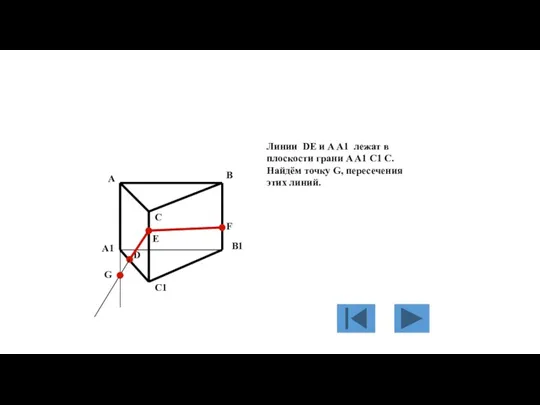
- 138. Точки E и F принадлежат плоскости грани B C C1 B1 и плоскости сечения, следовательно линия
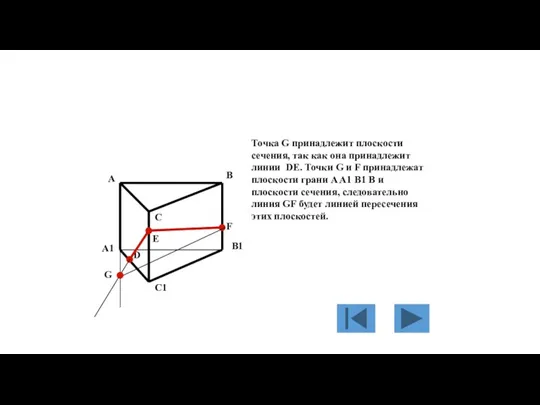
- 139. Линии DE и A A1 лежат в плоскости грани A A1 C1 C. Найдём точку G,
- 140. Точка G принадлежит плоскости сечения, так как она принадлежит линии DE. Точки G и F принадлежат
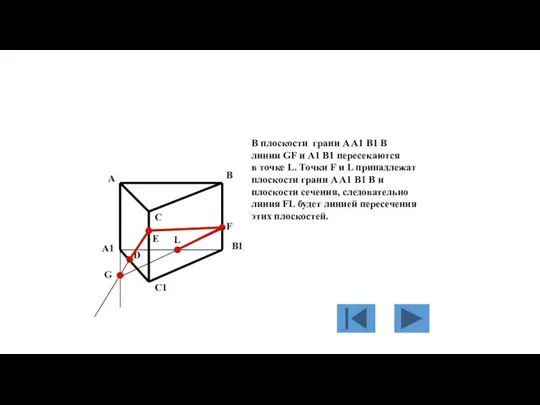
- 141. В плоскости грани A A1 B1 B линии GF и A1 B1 пересекаются в точке L.
- 142. Точки D и L принадлежат плоскости основания призмы A1 B1 C1 и плоскости сечения, следовательно линия
- 143. А четырёхугольник DEFL будет искомым сечением трёхгранной призмы плоскостью, проходящеё через три заданные точки D,E,F. A
- 145. Площади поверхностей многогранников
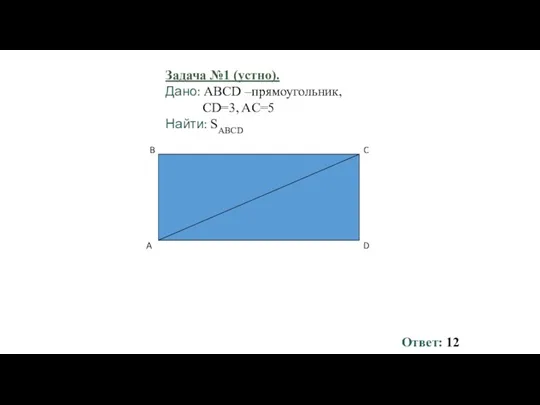
- 146. Задача №1 (устно). Дано: ABCD –прямоугольник, CD=3, AC=5 Найти: SABCD Ответ: 12
- 147. Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями. Многогранником называется тело, поверхность которого состоит
- 148. ПЛОЩАДЬ ПОВЕРХНОСТИ Площадью поверхности многогранника по определению считается сумма площадей, входящих в эту поверхность многоугольников. Площадь
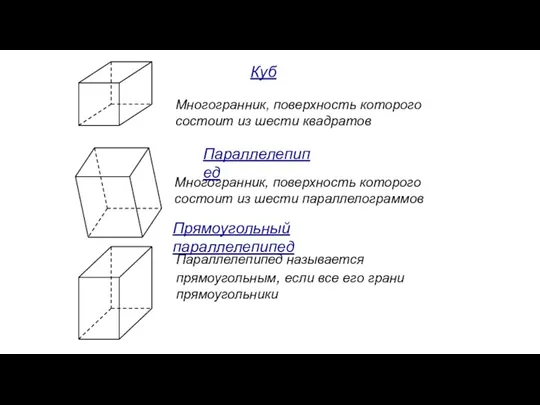
- 149. Многогранник, поверхность которого состоит из шести квадратов Многогранник, поверхность которого состоит из шести параллелограммов Параллелепипед называется
- 150. Площадь призмы Sбок. + 2Sосн Sбок. = Ph a b h Теорема: Площадь боковой поверхности прямой
- 151. Многогранник, поверхность которого состоит из многоугольника и треугольников, имеющих общую вершину Многоугольник называют основанием пирамиды Треугольники
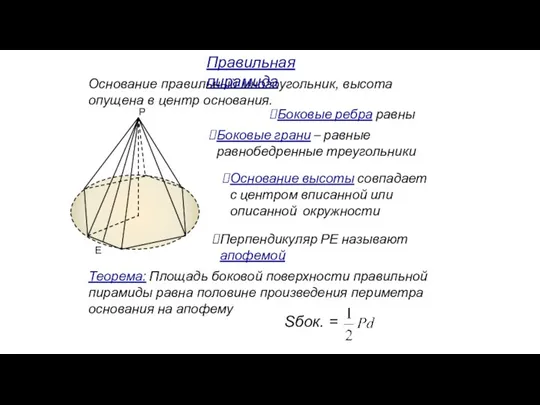
- 152. Основание правильный многоугольник, высота опущена в центр основания. Перпендикуляр РЕ называют апофемой Теорема: Площадь боковой поверхности
- 153. Правильные многогранники
- 154. Теорема Эйлера Число граней + число вершин - число ребер = 2. 4 4 6 8
- 155. Упражнение 1 Чему равна площадь поверхности куба с ребром 1? Ответ: 6.
- 156. Упражнение 2 Объем куба равен 8 м3. Найдите площадь его поверхности. Ответ: 24 м2.
- 157. Упражнение 3 Как изменится площадь поверхности куба, если каждое его ребро увеличить в: а) 2 раза;
- 158. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 6
- 159. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 7
- 160. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 8
- 161. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Упражнение 9
- 162. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 10
- 163. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 11
- 164. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ. 48. Упражнение 12
- 165. В каждой грани куба с ребром 6 см проделали сквозное квадратное отверстие со стороной квадрата 2
- 166. Упражнение 14 Чему равна площадь поверхности правильного тетраэдра с ребром 1?
- 167. Упражнение 15 Чему равна площадь поверхности октаэдра с ребром 1?
- 168. Упражнение 16 Чему равна площадь поверхности икосаэдра с ребром 1?
- 169. Упражнение 17 Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а
- 170. Упражнение 18 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см,
- 171. Упражнение 19 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями 6 см
- 172. Упражнение 20 Найдите площадь боковой поверхности правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и
- 173. Упражнение 21 Найдите площадь боковой поверхности правильной треугольной пирамиды со стороной основания 6 см и высотой
- 174. Упражнение 22 Найдите площадь боковой поверхности правильной шестиугольной пирамиды со стороной основания 4 см и высотой
- 176. Скачать презентацию


































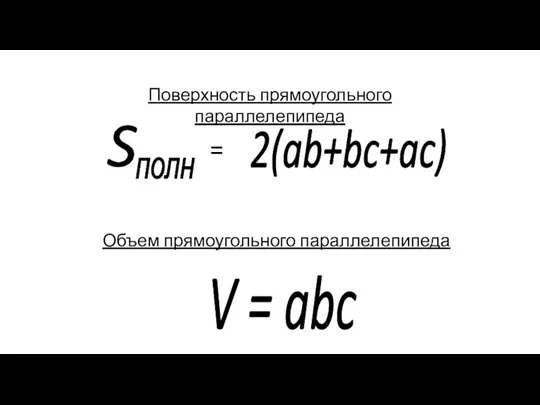





































































 Тригонометрия в ладони
Тригонометрия в ладони Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел 1 класс. Интерактивный тренажер Черничная полянка (прибавление числа 3)
1 класс. Интерактивный тренажер Черничная полянка (прибавление числа 3) Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления
Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления Таблица сложения
Таблица сложения Решение линейных уравнений с параметрами
Решение линейных уравнений с параметрами Метод найменших квадратів. (Тема 4)
Метод найменших квадратів. (Тема 4) Презентация к открытому уроку математики 1 класс ФГОС УМК ПНШ по теме Однозначные числа
Презентация к открытому уроку математики 1 класс ФГОС УМК ПНШ по теме Однозначные числа Признаки равенства прямоуголных треугольников. 7 класс
Признаки равенства прямоуголных треугольников. 7 класс Решение систем уравнений графическим способом
Решение систем уравнений графическим способом Деление обыкновенных дробей. 5 класс
Деление обыкновенных дробей. 5 класс Решение задач и выражений. 1 класс
Решение задач и выражений. 1 класс Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Презентация Прямая (геометрический материал)
Презентация Прямая (геометрический материал) Решение неравенств методом интервалов, 9 класс
Решение неравенств методом интервалов, 9 класс Степенные производные функции комплексных переменных
Степенные производные функции комплексных переменных Числа. Целые и рациональные числа. Действительные числа
Числа. Целые и рациональные числа. Действительные числа Симметрия в пространстве. Симметрия в природе и на практике
Симметрия в пространстве. Симметрия в природе и на практике Натуральные числа. Десятичная система счисления
Натуральные числа. Десятичная система счисления Приёмы устных вычислений вида 240 умножить на 4
Приёмы устных вычислений вида 240 умножить на 4 Математическая разминка по темам Арифметические действия над числами, Дроби.
Математическая разминка по темам Арифметические действия над числами, Дроби. Решение текстовых задач
Решение текстовых задач Отображения (функции) как отношения
Отображения (функции) как отношения Неделя математики в школе
Неделя математики в школе Метод логических рассуждений
Метод логических рассуждений Таблица умножения. Разминка
Таблица умножения. Разминка Диагностическая работа №2 школа 21 века
Диагностическая работа №2 школа 21 века Применение математических методов в биологии и в медицине
Применение математических методов в биологии и в медицине