Содержание
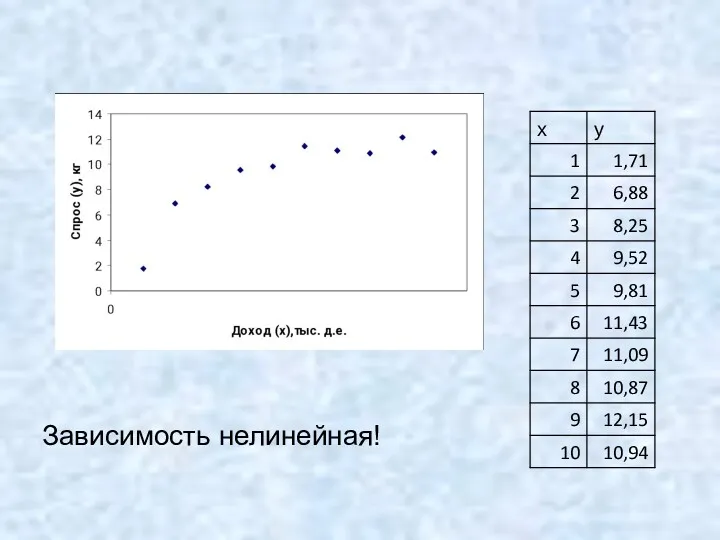
- 2. Зависимость нелинейная!
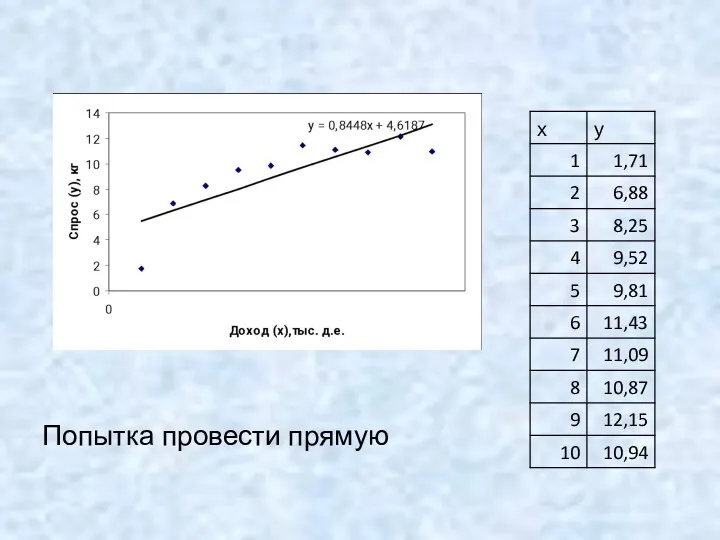
- 3. Попытка провести прямую
- 4. 1) Логарифмическая модель Для оценки такой зависимости создаем столбец с ln(x)
- 5. 1) Логарифмическая модель Используя сервис Анализ данных построим модель линейной регрессии, используя в качестве зависимой переменной
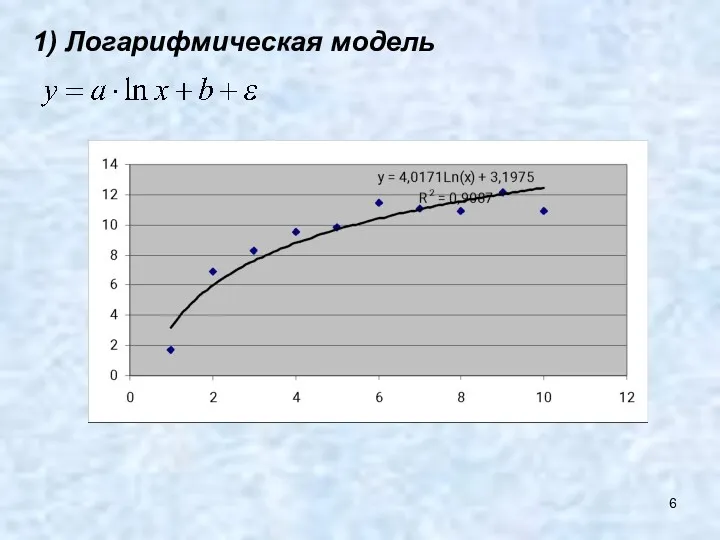
- 6. 1) Логарифмическая модель
- 7. 1) Логарифмическая модель Интерпретация коэффициента а: при увеличении х на 1% y увеличится на а/100 единиц.
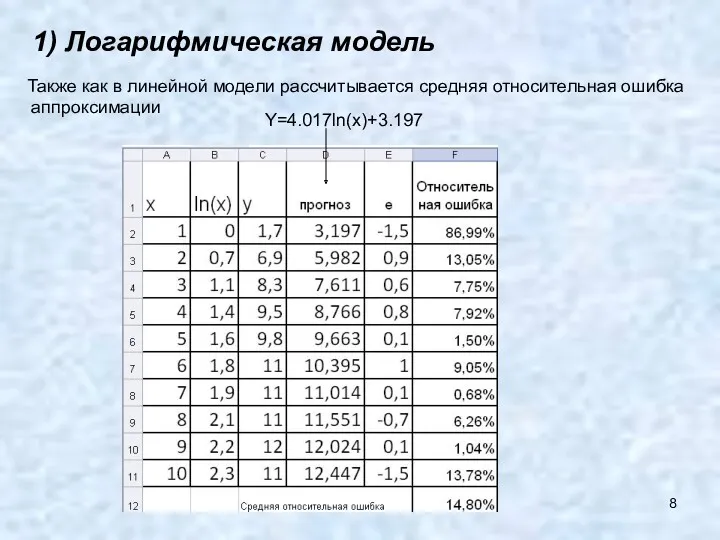
- 8. 1) Логарифмическая модель Также как в линейной модели рассчитывается средняя относительная ошибка аппроксимации Y=4.017ln(x)+3.197
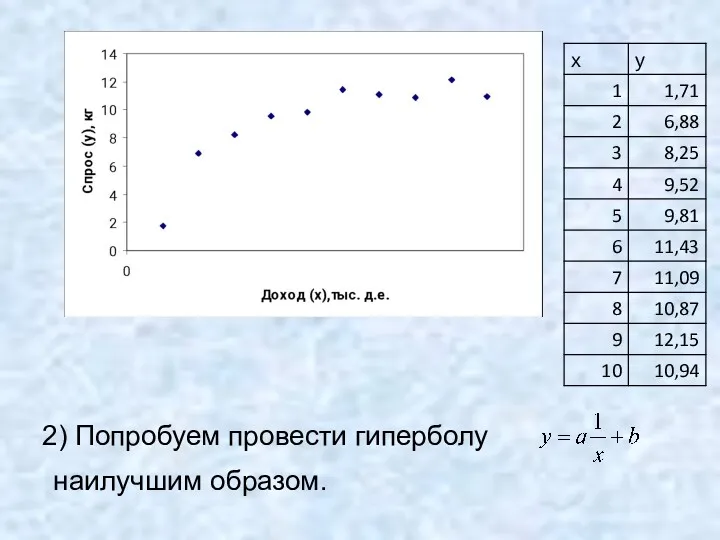
- 9. 2) Попробуем провести гиперболу наилучшим образом.
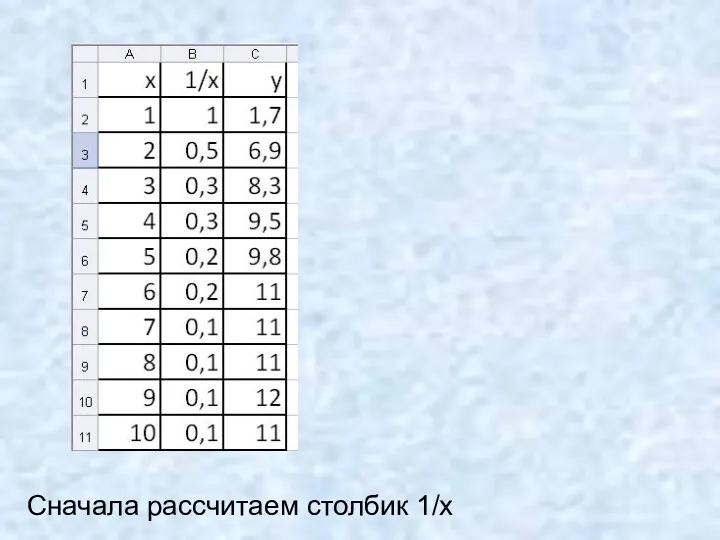
- 10. Сначала рассчитаем столбик 1/x
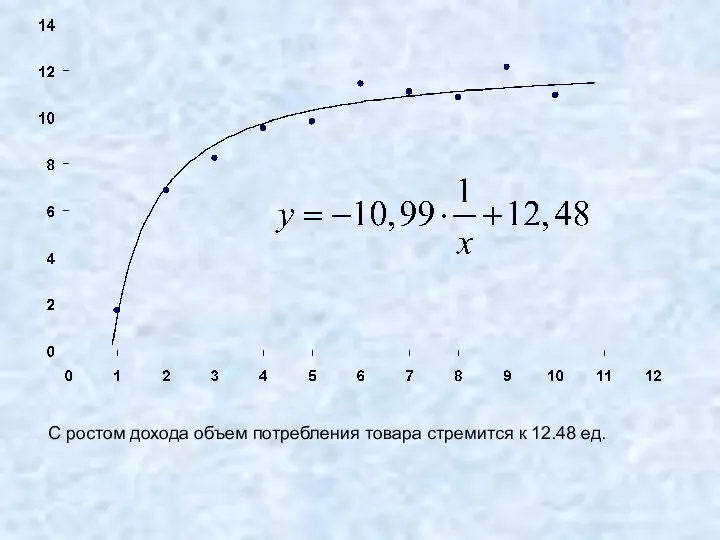
- 12. С ростом дохода объем потребления товара стремится к 12.48 ед.
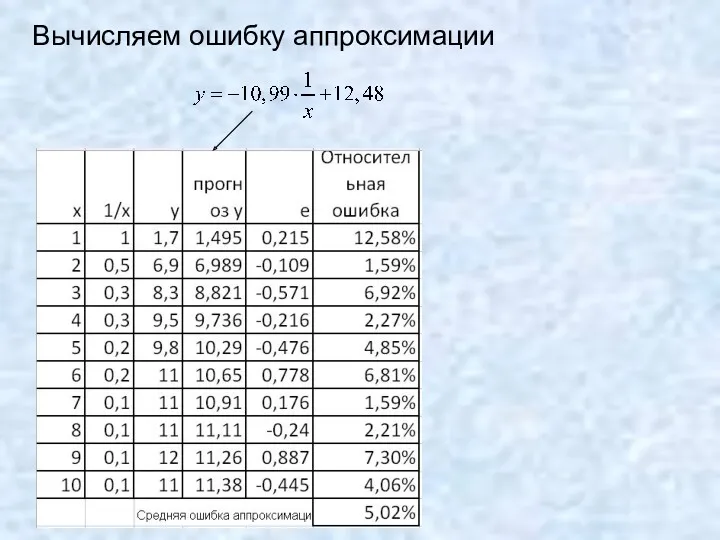
- 13. Вычисляем ошибку аппроксимации
- 14. 3) Степенная модель Интерпретация коэффициента a – эластичность зависимой переменной по объясняющей переменной a показывает, на
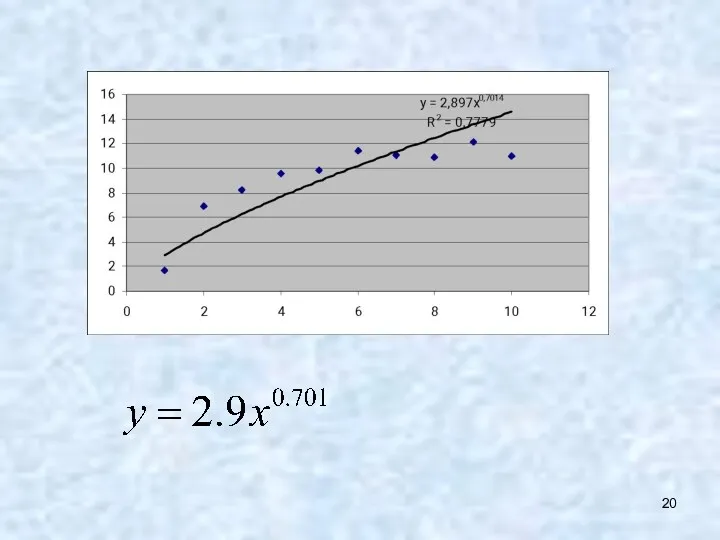
- 15. Степенная модель Сводится к линейной модели логарифмированием
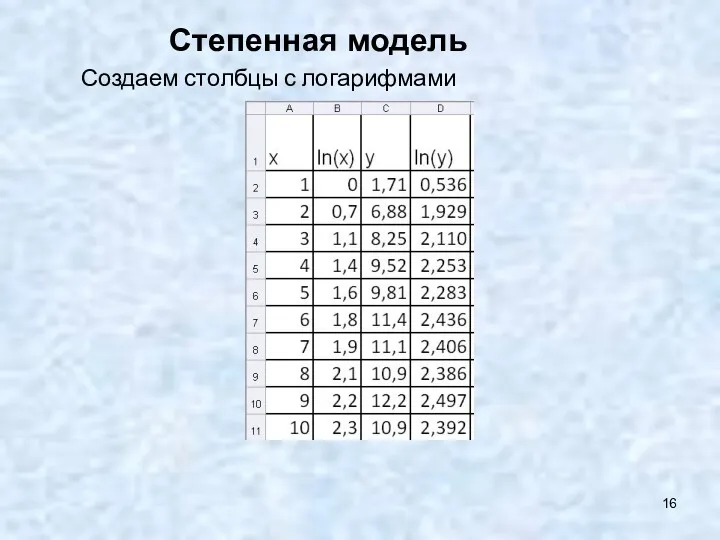
- 16. Степенная модель Создаем столбцы с логарифмами
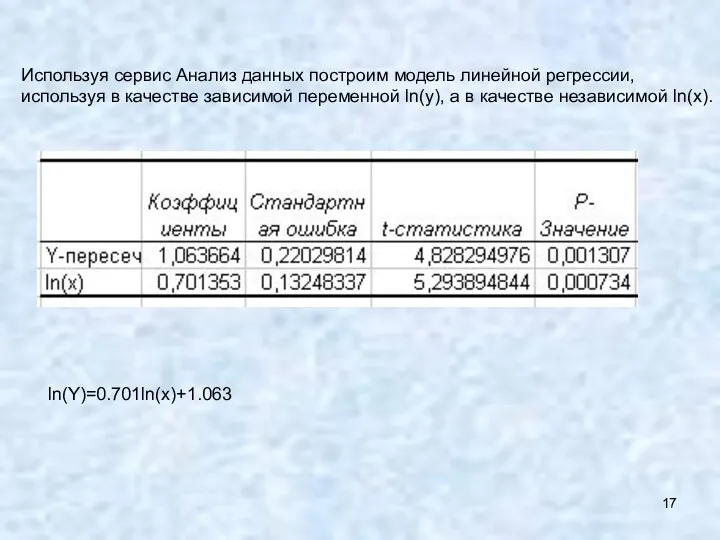
- 17. Используя сервис Анализ данных построим модель линейной регрессии, используя в качестве зависимой переменной ln(y), а в
- 18. Используя сервис Анализ данных построим модель линейной регрессии, используя в качестве зависимой переменной ln(y), а в
- 19. Используя сервис Анализ данных построим модель линейной регрессии, используя в качестве зависимой переменной ln(y), а в
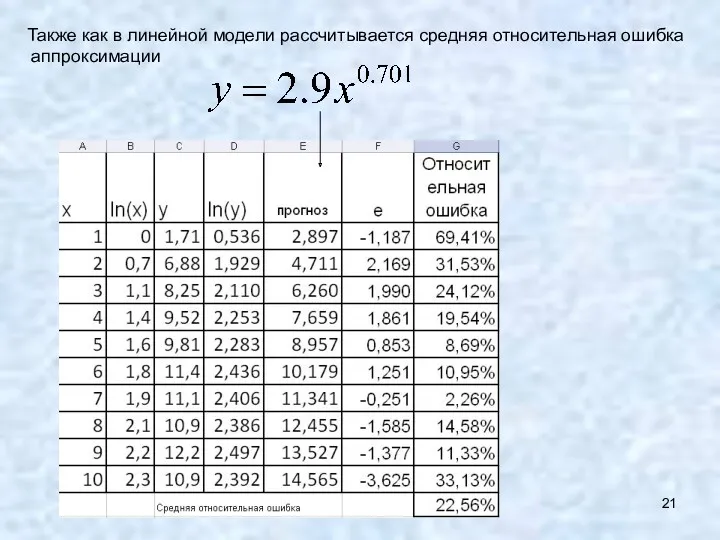
- 21. Также как в линейной модели рассчитывается средняя относительная ошибка аппроксимации
- 22. - наилучшая функция спроса в зависимости от дохода. Выполнить прогноз потребления продукта домохозяйством с доходом 4
- 23. Модели парной нелинейной регрессии Существует 2 типа нелинейных моделей: модели, сводящиеся к линейным; модели, не сводящиеся
- 24. 1 тип моделей 1) Гиперболическая модель
- 25. 1 тип моделей 3) Экспоненциальная модель
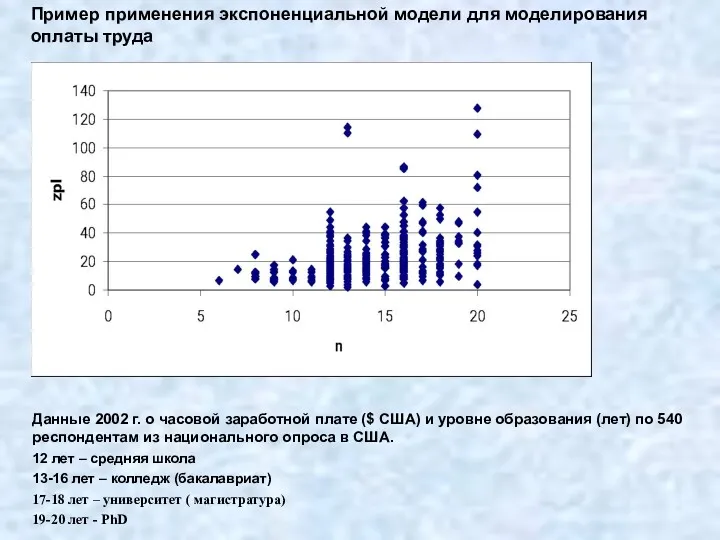
- 26. Пример применения экспоненциальной модели для моделирования оплаты труда Данные 2002 г. о часовой заработной плате ($
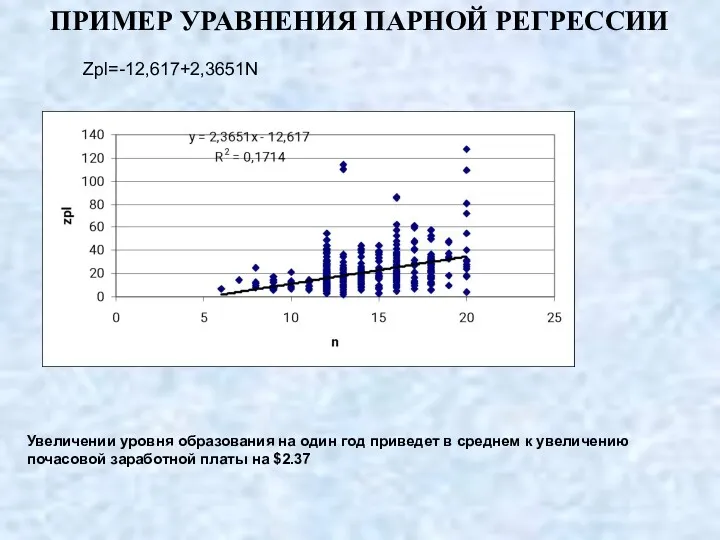
- 27. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ Zpl=-12,617+2,3651N Увеличении уровня образования на один год приведет в среднем к увеличению
- 28. Пример применения экспоненциальной модели для моделирования оплаты труда
- 29. Пример применения экспоненциальной модели для моделирования оплаты труда
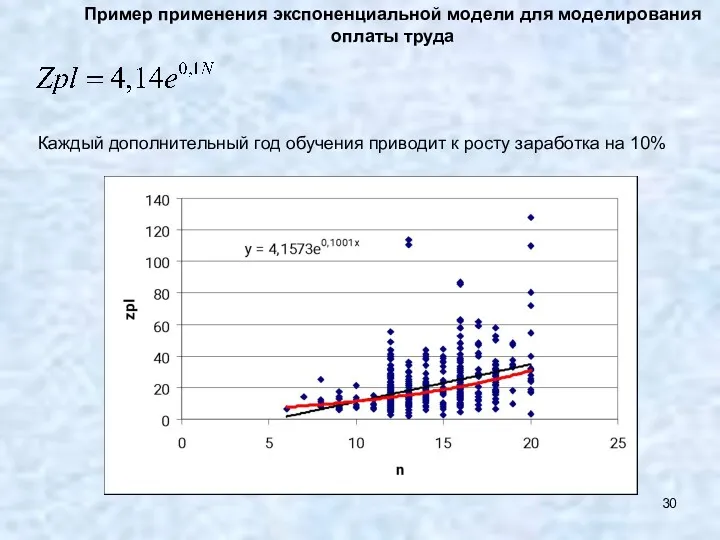
- 30. Пример применения экспоненциальной модели для моделирования оплаты труда Каждый дополнительный год обучения приводит к росту заработка
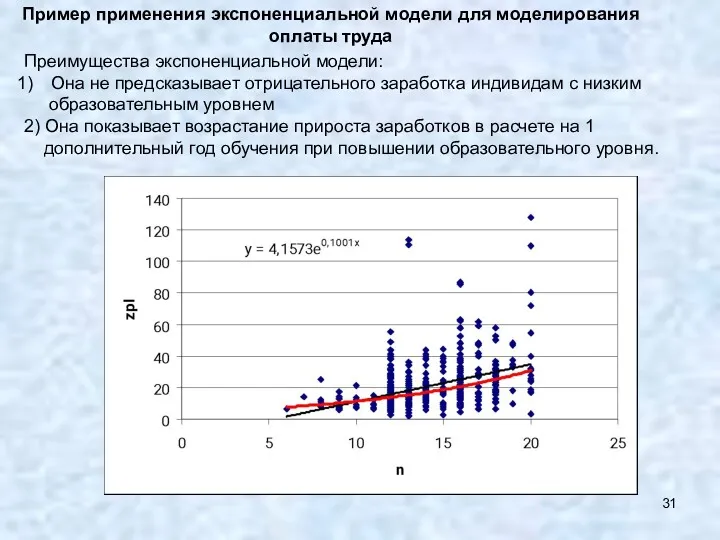
- 31. Пример применения экспоненциальной модели для моделирования оплаты труда Преимущества экспоненциальной модели: Она не предсказывает отрицательного заработка
- 32. 4) Степенная модель
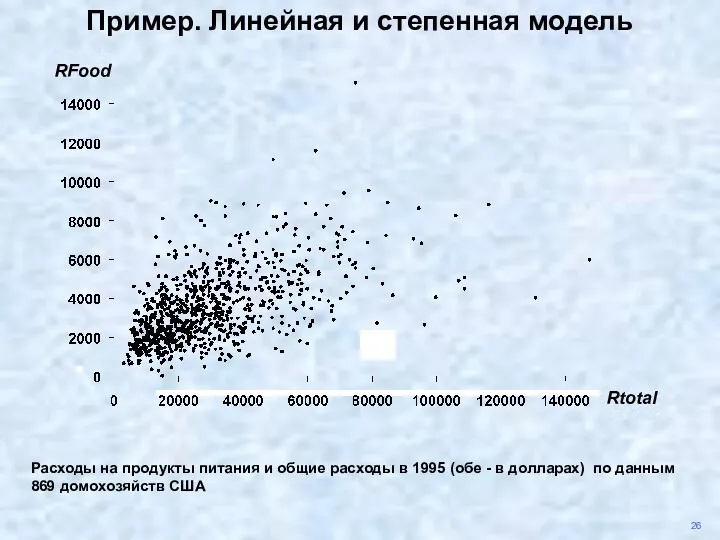
- 33. 26 Пример. Линейная и степенная модель Расходы на продукты питания и общие расходы в 1995 (обе
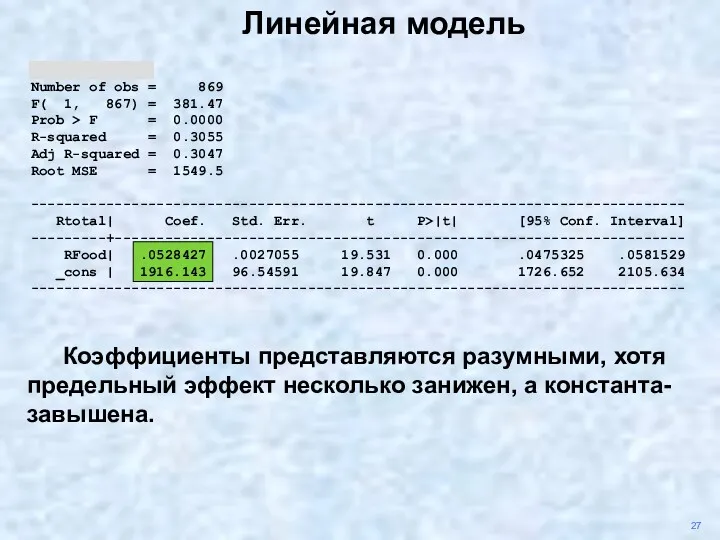
- 34. Number of obs = 869 F( 1, 867) = 381.47 Prob > F = 0.0000 R-squared
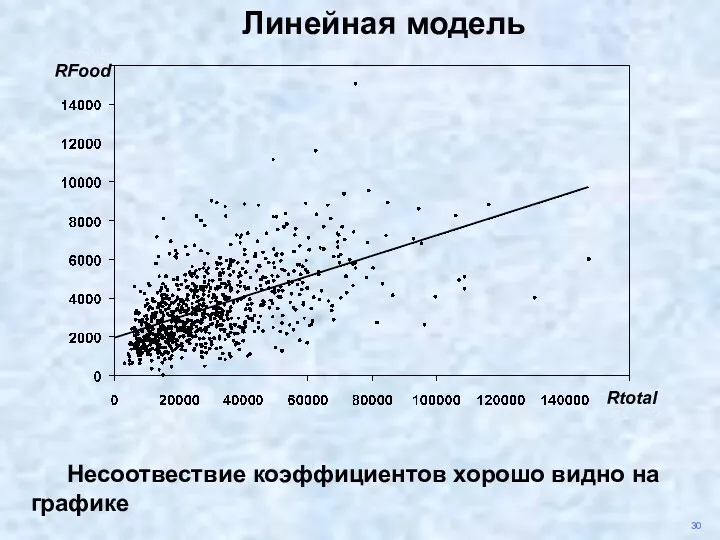
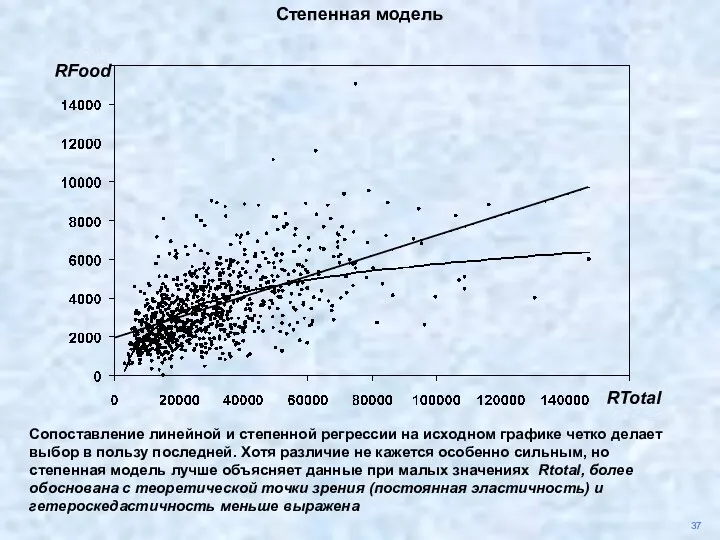
- 35. 30 Несоотвествие коэффициентов хорошо видно на графике Rtotal RFood Линейная модель
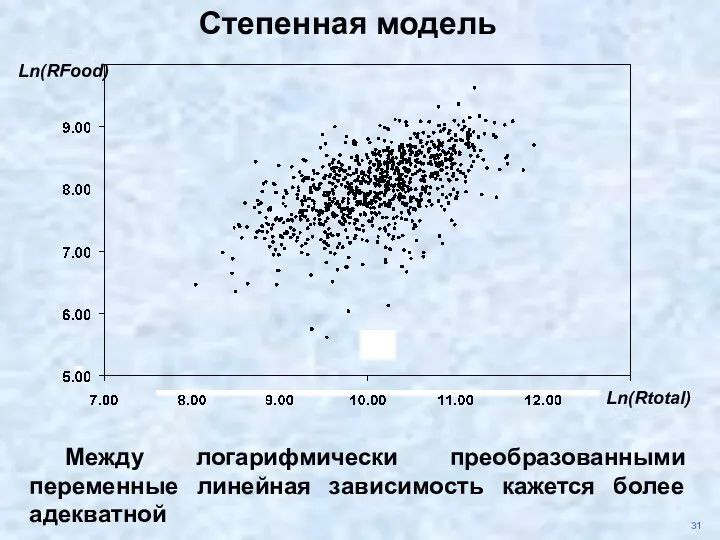
- 36. 31 Степенная модель Между логарифмически преобразованными переменные линейная зависимость кажется более адекватной Ln(RFood) Ln(Rtotal)
- 37. 32 Модель высокозначима. Коэффициент эластичности расходов на товары питания по совокупным расходам положителен и меньше единицы,
- 38. 37 Степенная модель Сопоставление линейной и степенной регрессии на исходном графике четко делает выбор в пользу
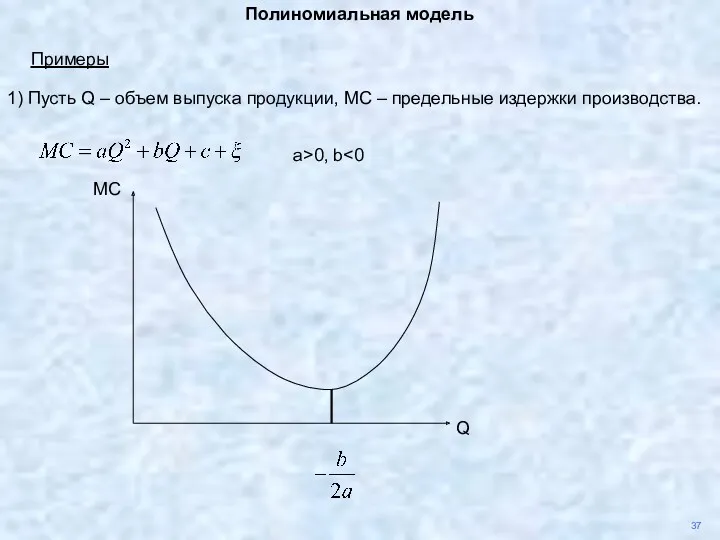
- 39. 37 Полиномиальная модель Появляются возможность исследования зависимостей, для которых существенно наличие максимумов и минимумов квадратичная модель
- 40. 37 Полиномиальная модель - модель множественной регрессии.
- 41. 37 Полиномиальная модель Примеры 1) Пусть Q – объем выпуска продукции, MC – предельные издержки производства.
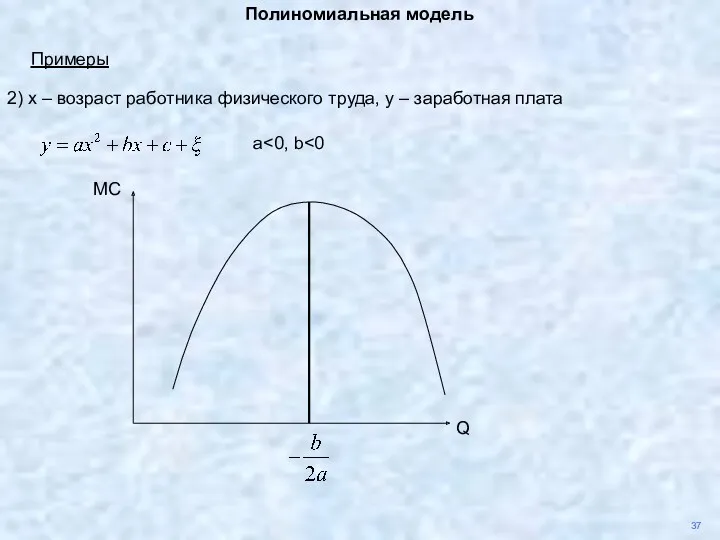
- 42. 37 Полиномиальная модель Примеры 2) x – возраст работника физического труда, y – заработная плата a
- 43. 2 тип моделей (модели, не сводящиеся к линейным) Например, Логистическая модель a
- 45. Скачать презентацию



















 Начальные геометрические сведения
Начальные геометрические сведения Игры для детей
Игры для детей Танграм. Внеурочное занятие по математике
Танграм. Внеурочное занятие по математике Урок математики в 4 классе по ОС школа 2100 Тема: Арифметические действия над числами.
Урок математики в 4 классе по ОС школа 2100 Тема: Арифметические действия над числами. Конспект урока по математике по теме Урок- путешествие в космос. Закрепление знаний таблицы сложения с переходом через десяток.1 класс.
Конспект урока по математике по теме Урок- путешествие в космос. Закрепление знаний таблицы сложения с переходом через десяток.1 класс. Закрепление. Величины (Методическая разработка)
Закрепление. Величины (Методическая разработка) Определение подобных треугольников. (Упражнение 9. 8 класс)
Определение подобных треугольников. (Упражнение 9. 8 класс) Счет до 10
Счет до 10 Нахождение дроби от числа. Демонстрационный материал. 6 класс
Нахождение дроби от числа. Демонстрационный материал. 6 класс Задачи 1 класс
Задачи 1 класс Метод интервалов решения дробно-рациональных неравенств
Метод интервалов решения дробно-рациональных неравенств Решение квадратных уравнений. Алгебра 8 класс
Решение квадратных уравнений. Алгебра 8 класс Задач на проценты
Задач на проценты Показательная функция
Показательная функция Число 6. Цифра 6.
Число 6. Цифра 6. Решение задач с помощью уравнений. 6 класс
Решение задач с помощью уравнений. 6 класс Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой Измерение углов
Измерение углов Дії з векторами у просторі (правила додавання)
Дії з векторами у просторі (правила додавання) Математика. Решение задач. Закрепление
Математика. Решение задач. Закрепление Прогрессии вокруг нас
Прогрессии вокруг нас Правильные многогранники
Правильные многогранники Сложение, вычитание и умножение чисел с разными знаками. Урок математики в 6 классе
Сложение, вычитание и умножение чисел с разными знаками. Урок математики в 6 классе Признаки делимости натуральных чисел
Признаки делимости натуральных чисел Графы. Основные понятия
Графы. Основные понятия Варряд
Варряд Теорема Фалеса
Теорема Фалеса Умножение и деление десятичной дроби на 10, 100, 1000
Умножение и деление десятичной дроби на 10, 100, 1000